Opérations sur les ensembles : union, intersection, complément et différence

Un ensemble est une collection d’éléments.

Nous désignons un ensemble par une lettre majuscule et nous définissons les éléments de l’ensemble à l’aide d’accolades. Par exemple, supposons que nous ayons un ensemble appelé « A » avec les éléments 1, 2, 3. Nous écririons ceci comme suit :

UNE = {1, 2, 3}

Ce didacticiel explique les opérations sur les ensembles les plus couramment utilisées en probabilités et en statistiques.

syndicat

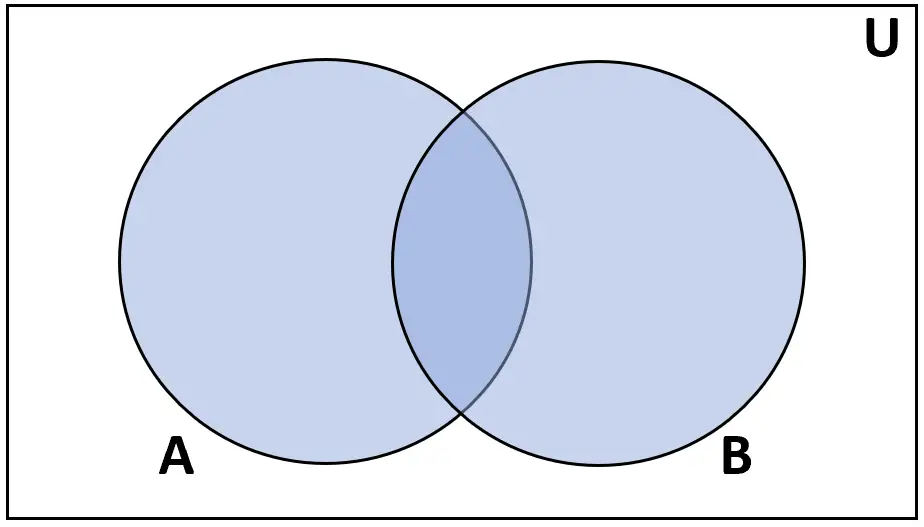
Définition : L’ union des ensembles A et B est l’ensemble des éléments qui se trouvent soit dans A, soit dans B.

Notation : A ∪ B

Exemples:

• {1, 2, 3} ∪ {4, 5, 6} = {1, 2, 3, 4, 5, 6}
• {1, 2} ∪ {1, 2} = {1, 2}
• {1, 2, 3} ∪ {3, 4} = {1, 2, 3, 4}

Intersection

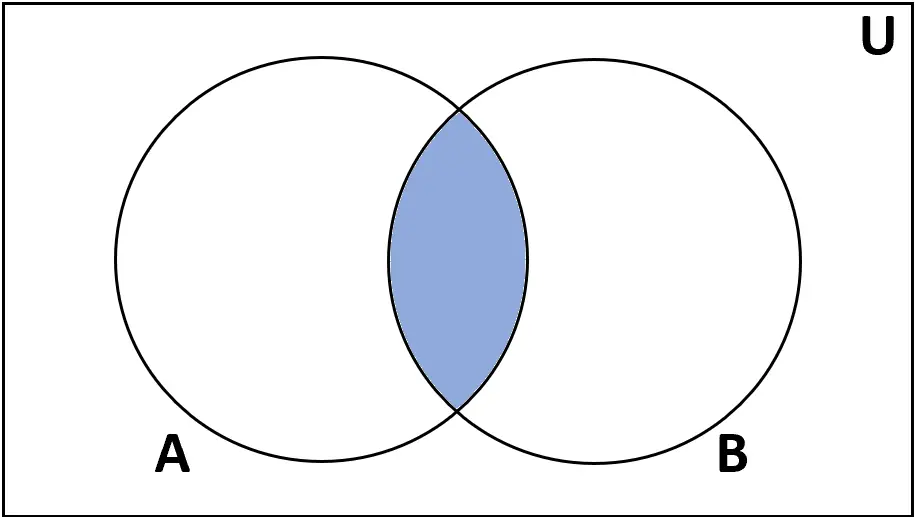
Définition : L’ intersection des ensembles A et B est l’ensemble des éléments qui se trouvent à la fois dans A et B.

Notation : A ∩ B

Exemples:

• {1, 2, 3} ∩ {4, 5, 6} = {∅}
• {1, 2} ∩ {1, 2} = {1, 2}
• {1, 2, 3} ∩ {3, 4} = {3}

Complément

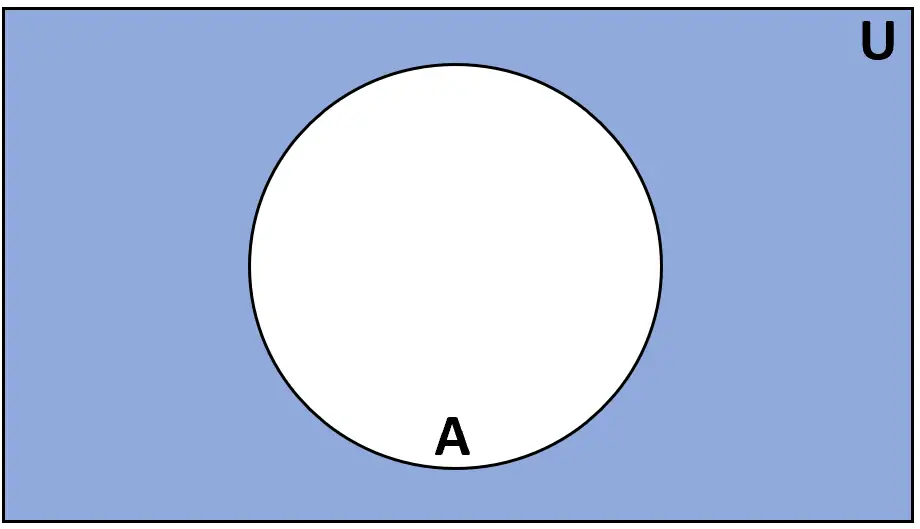
Définition : Le complément de l’ensemble A est l’ensemble des éléments qui sont dans l’ensemble universel U mais ne sont pas dans A.

Notation : A’ ou ^Ac

Exemples:

• Si U = {1, 2, 3, 4, 5, 6} et A = {1, 2}, alors A ^c = {3, 4, 5, 6}
• Si U = {1, 2, 3} et A = {1, 2}, alors A ^c = {3}

Différence

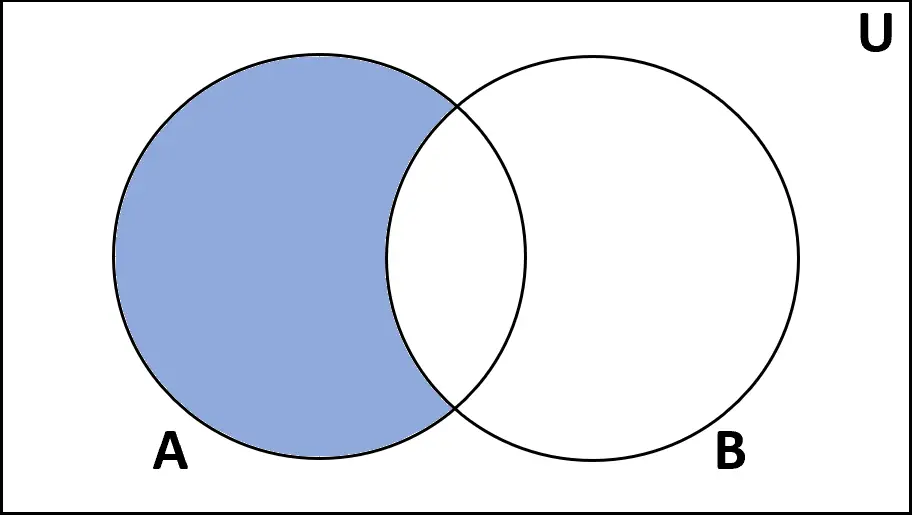
Définition : La différence entre les ensembles A et B est l’ensemble des éléments qui se trouvent dans A mais pas dans B.

Notations : A – B

Exemples:

• {1, 2, 3} – {2, 3, 4} = {1}
• {1, 2} – {1, 2} = {∅}
• {1, 2, 3} – {4, 5} = {1, 2, 3}

Différence symétrique

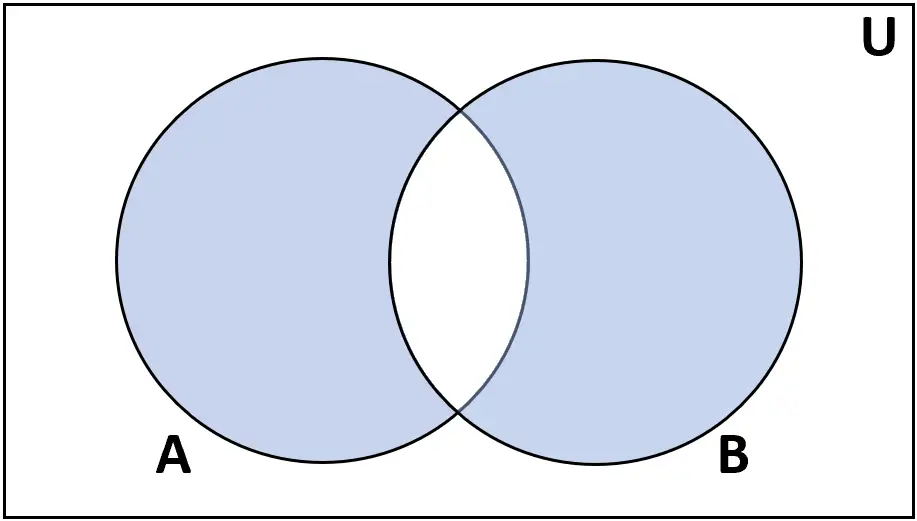
Définition : La différence symétrique des ensembles A et B est l’ensemble des éléments qui se trouvent soit dans A, soit dans B, mais pas dans les deux.

Notation : AΔB

Exemples:

• {1, 2, 3} Δ {2, 3, 4} = {1, 4}
• {1, 2} Δ {1, 2} = {∅}
• {1, 2, 3} Δ {4, 5} = {1, 2, 3, 4, 5}

Produit cartésien

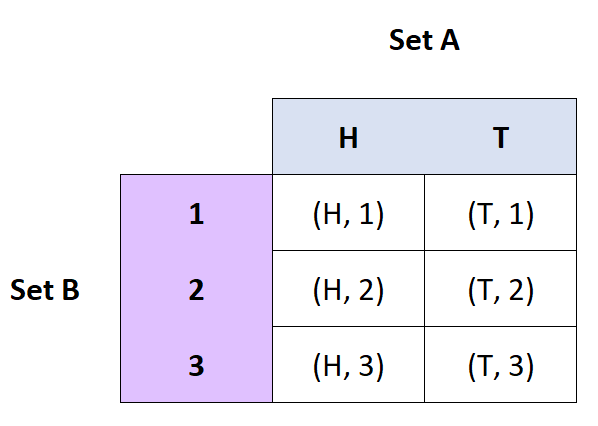
Définition : Le produit cartésien des ensembles A et B est l’ensemble des paires ordonnées de A et B.

Notation : A x B

Exemples:

• Si A = {H, T} et B = {1, 2, 3}, alors A x B = {(H, 1), (H, 2), (H, 3), (T, 1), ( T, 2), (T, 3)}
• Si A = {T, H} et B = {1, 2, 3}, alors A x B = {(T, 1), (T, 2), (T, 3), (H, 1), ( H, 2), (H, 3)}