Comment effectuer un test F partiel dans Excel

Un test F partiel est utilisé pour déterminer s’il existe ou non une différence statistiquement significative entre un modèle de régression et une version imbriquée du même modèle.

Un modèle imbriqué est simplement un modèle qui contient un sous-ensemble de variables prédictives dans le modèle de régression global.

Par exemple, supposons que nous ayons le modèle de régression suivant avec quatre variables prédictives :

Y = β ₀ + β ₁ x ₁ + β ₂ x ₂ + β ₃ x ₃ + β ₄ x ₄ + ε

Un exemple de modèle imbriqué serait le modèle suivant avec seulement deux des variables prédictives d’origine :

Y = β ₀ + β ₁ x ₁ + β ₂ x ₂ + ε

Pour déterminer si ces deux modèles sont significativement différents, nous pouvons effectuer un test F partiel, qui calcule la statistique de test F suivante :

F = ((RSS _réduit – RSS _complet )/p) / (RSS _complet /nk)

où:

• RSS _réduit : La somme résiduelle des carrés du modèle réduit (c’est-à-dire « imbriqué »).
• RSS _full : La somme des carrés résiduelle du modèle complet.
• p : nombre de prédicteurs supprimés du modèle complet.
• n : le nombre total d’observations dans l’ensemble de données.
• k : Le nombre de coefficients (y compris l’ordonnée à l’origine) dans le modèle complet.

Ce test utilise les hypothèses nulles et alternatives suivantes :

H ₀ : Tous les coefficients supprimés du modèle complet sont nuls.

H _A : Au moins un des coefficients supprimés du modèle complet est non nul.

Si la valeur p correspondant à la statistique du test F est inférieure à un certain niveau de signification (par exemple 0,05), alors nous pouvons rejeter l’hypothèse nulle et conclure qu’au moins un des coefficients supprimés du modèle complet est significatif.

L’exemple suivant montre comment effectuer un test F partiel dans Excel.

Exemple : test F partiel dans Excel

Supposons que nous ayons l’ensemble de données suivant dans Excel :

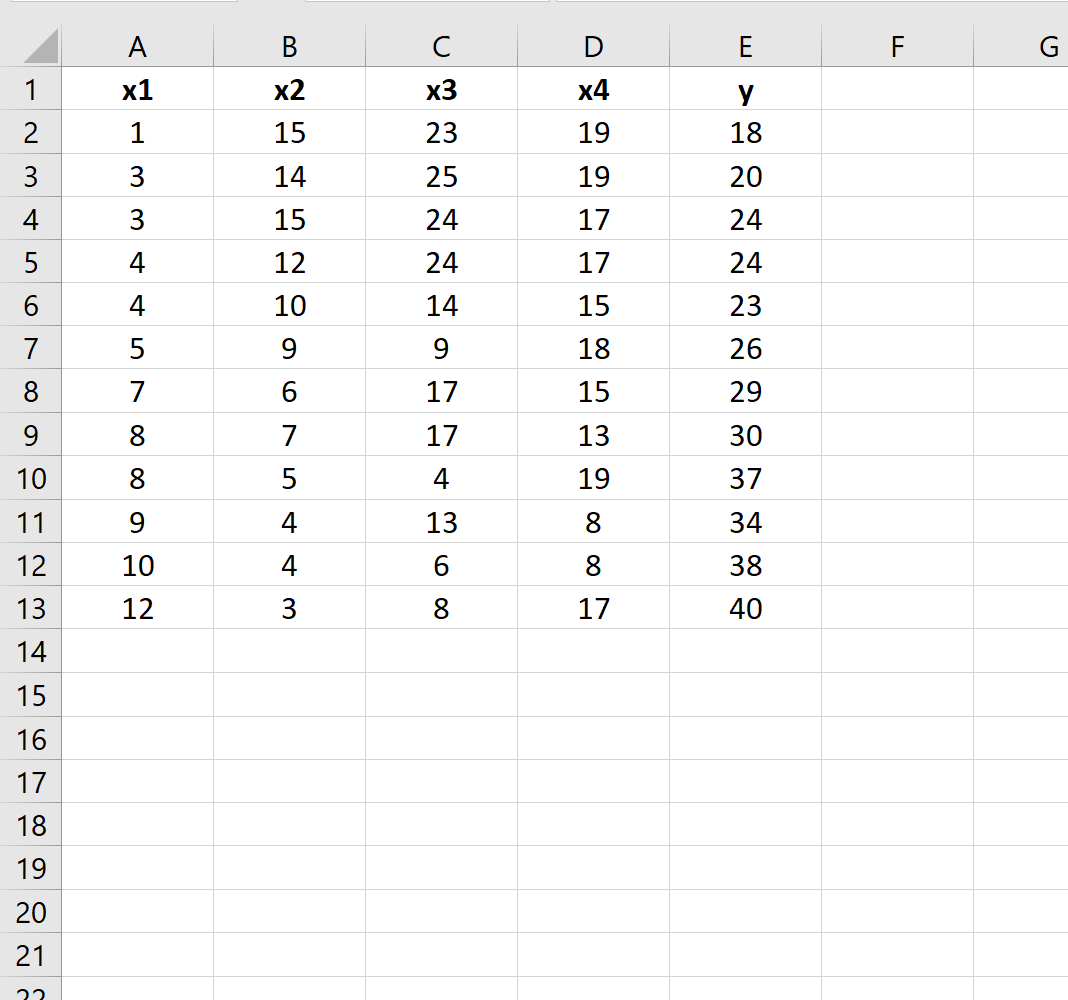
Supposons que nous souhaitions déterminer s’il existe une différence entre les deux modèles de régression suivants :

Modèle complet : y = β ₀ + β ₁ x ₁ + β ₂ x ₂ + β ₃ x ₃ + β ₄ x ₄

Modèle réduit : y = β ₀ + β ₁ x ₁ + β ₂ x ₂

Nous pouvons procéder àune régression linéaire multiple dans Excel pour chaque modèle pour obtenir le résultat suivant :

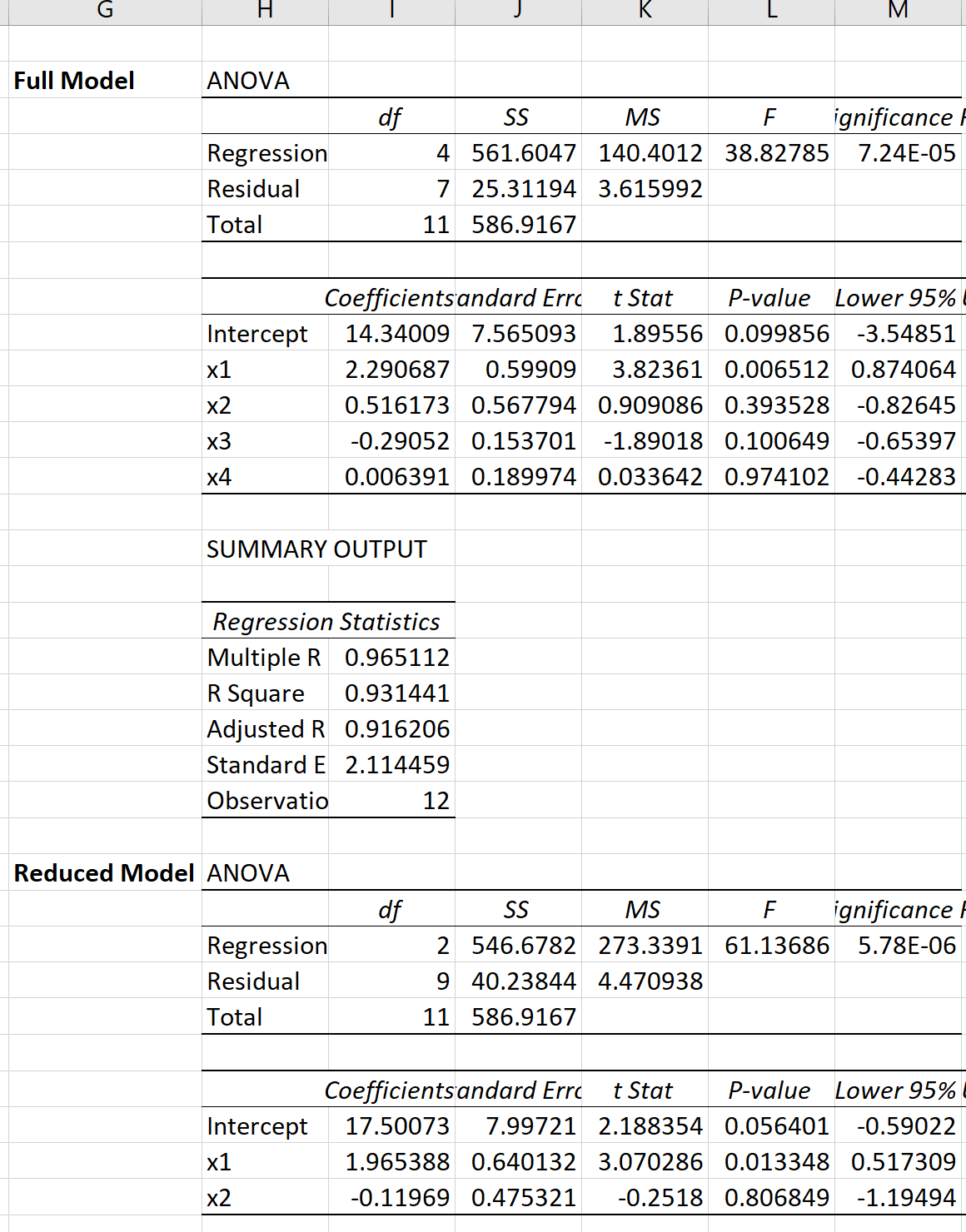
Nous pouvons ensuite utiliser la formule suivante pour calculer la statistique du test F pour le test F partiel :

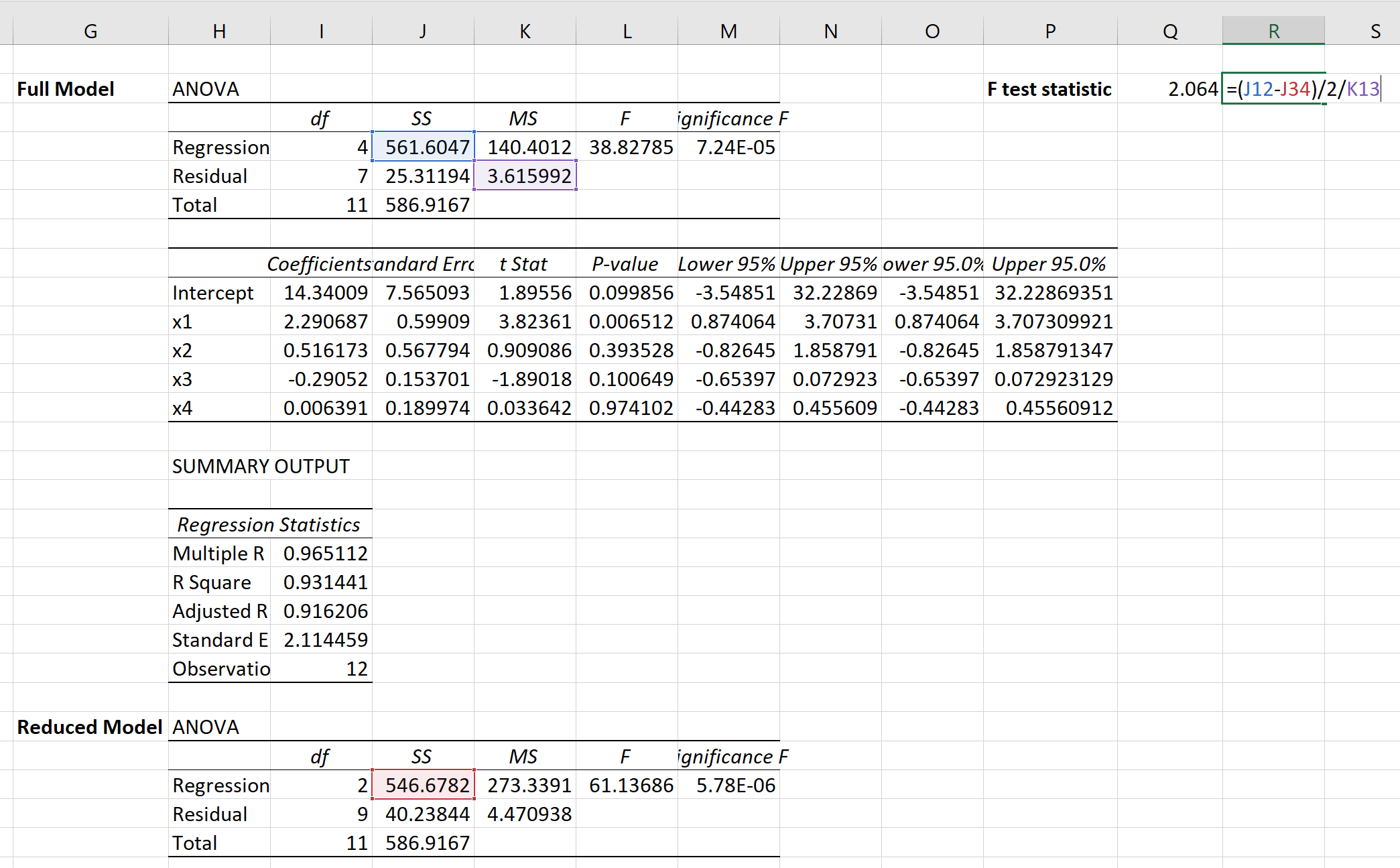
La statistique du test s’avère être 2,064 .

Nous pouvons alors utiliser la formule suivante pour calculer la valeur p correspondante :

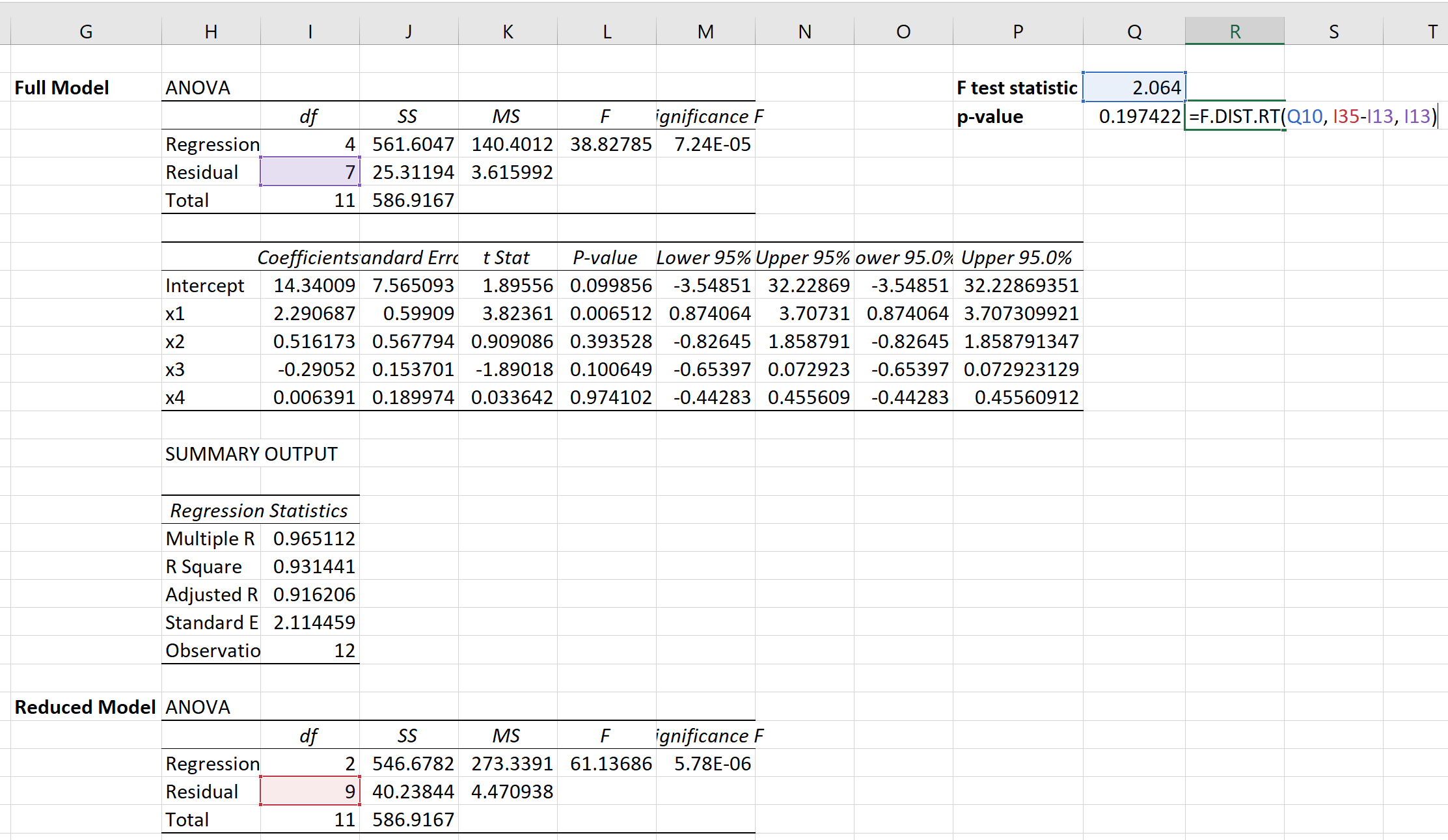
La valeur p s’avère être de 0,1974 .

Puisque cette valeur p n’est pas inférieure à 0,05, nous ne parviendrons pas à rejeter l’hypothèse nulle. Cela signifie que nous n’avons pas suffisamment de preuves pour affirmer que l’une ou l’autre des variables prédictives x3 ou x4 est statistiquement significative.

En d’autres termes, l’ajout de x3 et x4 au modèle de régression n’améliore pas significativement l’ajustement du modèle.

Ressources additionnelles

Comment effectuer une régression linéaire simple dans Excel
Comment effectuer une régression linéaire multiple dans Excel
Comment calculer l’erreur standard de régression dans Excel