Coefficient d’asymétrie de Pearson dans Excel (étape par étape)

Développé par le biostatisticien Karl Pearson , le coefficient d’asymétrie de Pearson est un moyen de mesurer l’ asymétrie dans un échantillon d’ensemble de données.

Il existe en fait deux méthodes qui peuvent être utilisées pour calculer le coefficient d’asymétrie de Pearson :

Méthode 1 : utiliser le mode

Asymétrie = (Moyenne – Mode) / Écart type de l’échantillon

Méthode 2 : utilisation de la médiane

Asymétrie = 3 (Moyenne – Médiane) / Écart type de l’échantillon

En général, la deuxième méthode est préférée car le mode n’est pas toujours une bonne indication de l’endroit où se situe la valeur « centrale » d’un ensemble de données et il peut y avoir plus d’un mode dans un ensemble de données donné.

L’exemple étape par étape suivant montre comment calculer les deux versions du coefficient d’asymétrie de Pearson pour un ensemble de données donné dans Excel.

Étape 1 : Créer l’ensemble de données

Tout d’abord, créons l’ensemble de données suivant dans Excel :

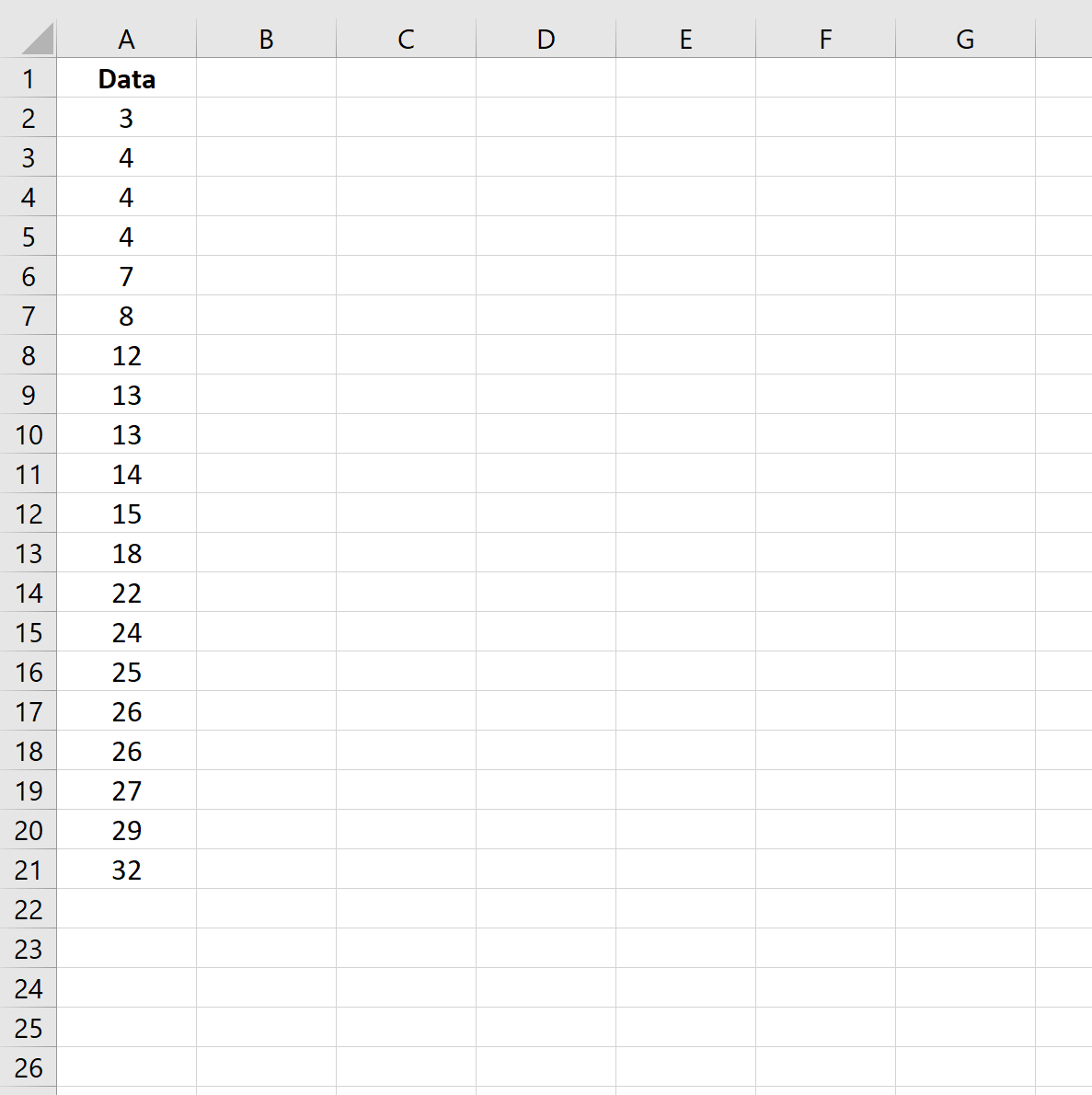
Étape 2 : Calculer le coefficient d’asymétrie de Pearson (à l’aide du mode)

Ensuite, nous pouvons utiliser la formule suivante pour calculer le coefficient d’asymétrie de Pearson en utilisant le mode :

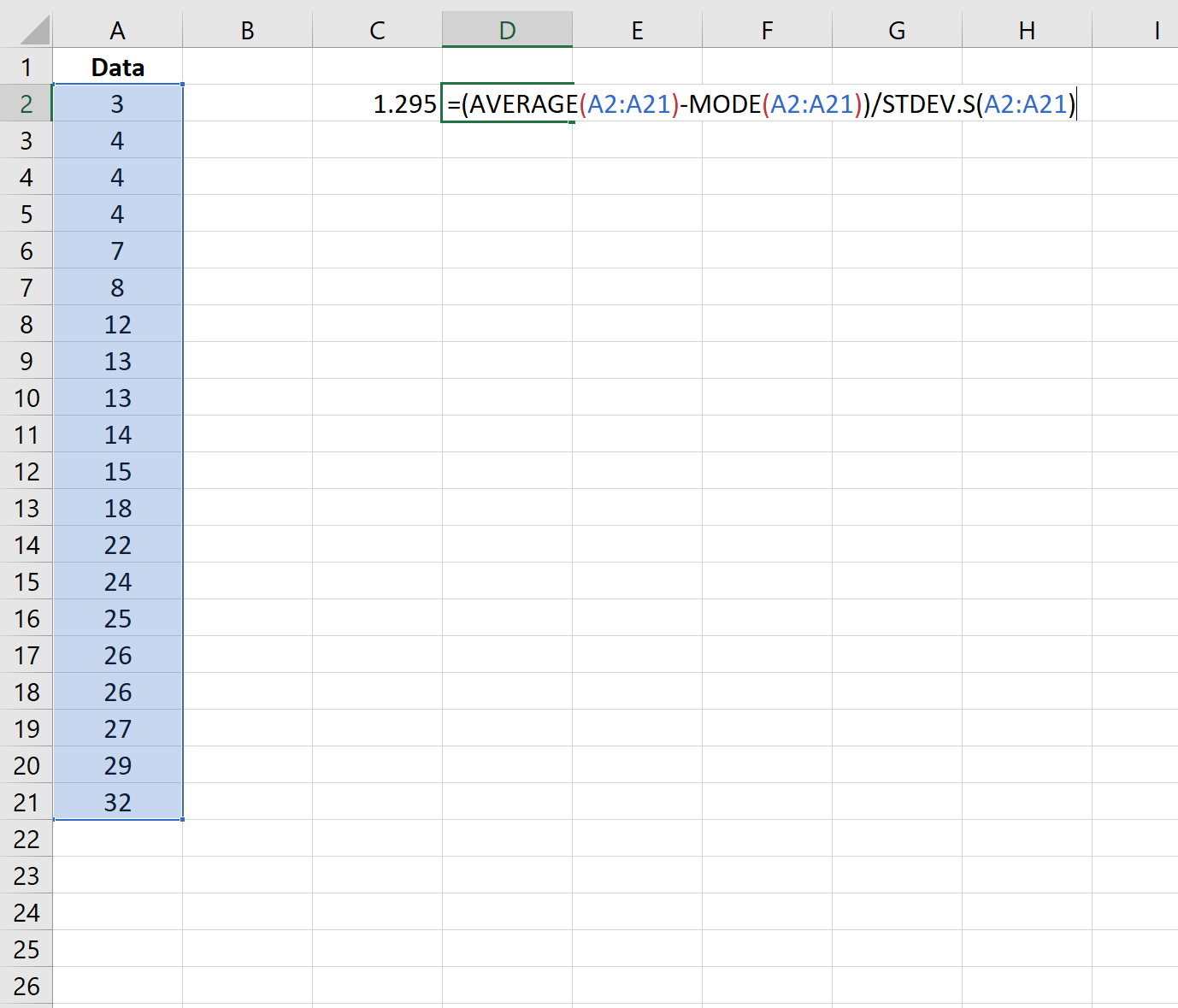
L’asymétrie s’avère être de 1,295 .

Étape 3 : Calculer le coefficient d’asymétrie de Pearson (à l’aide de la médiane)

Nous pouvons également utiliser la formule suivante pour calculer le coefficient d’asymétrie de Pearson en utilisant la médiane :

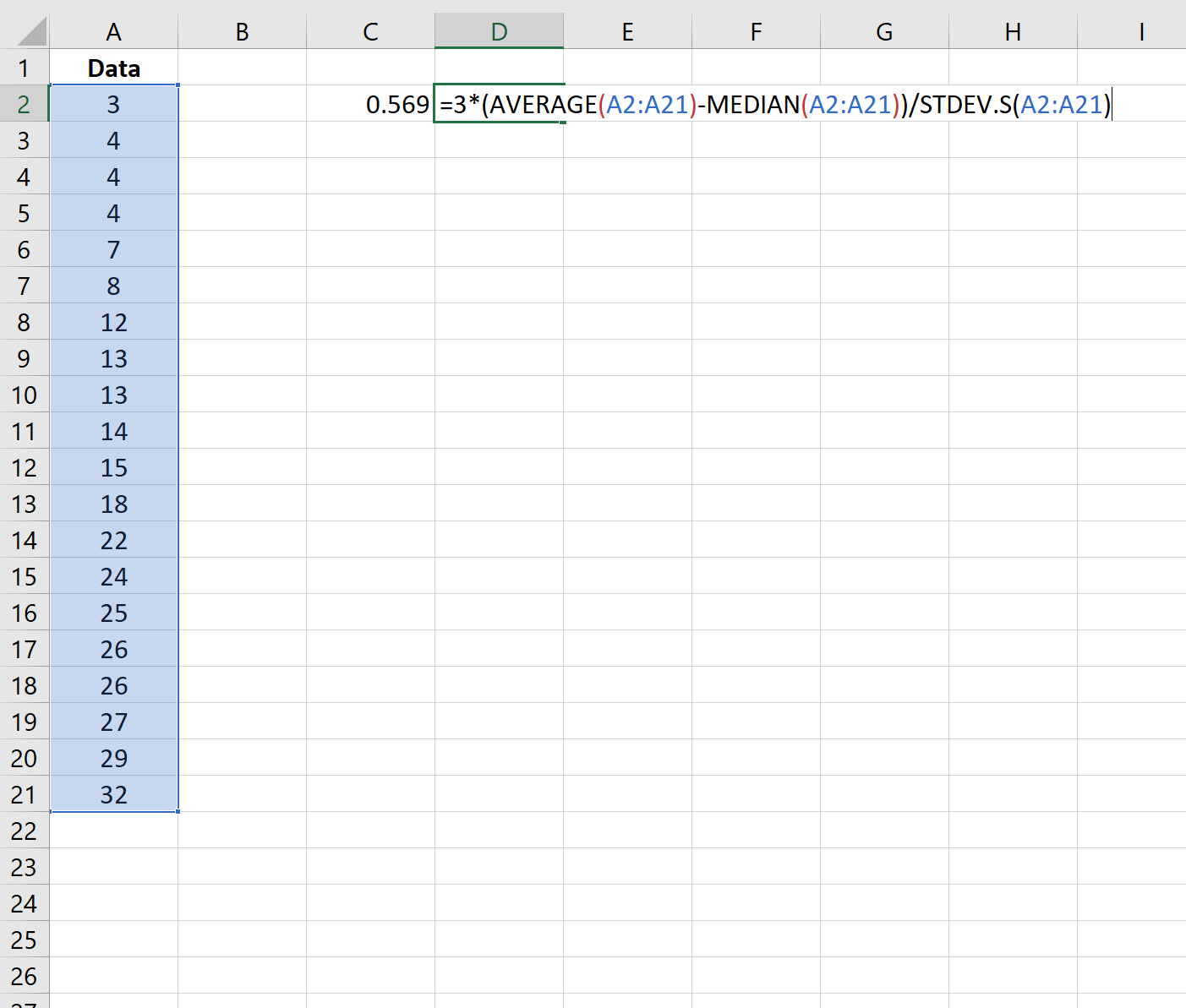
L’asymétrie s’avère être de 0,569 .

Comment interpréter l’asymétrie

Nous interprétons le coefficient d’asymétrie de Pearson des manières suivantes :

• Une valeur de 0 indique aucune asymétrie. Si nous créions un histogramme pour visualiser la distribution des valeurs dans un ensemble de données, il serait parfaitement symétrique.
• Une valeur positive indique une inclinaison positive ou une inclinaison « à droite ». Un histogramme révélerait une « queue » sur le côté droit de la distribution.
• Une valeur négative indique une inclinaison négative ou une inclinaison « gauche ». Un histogramme révélerait une « queue » sur le côté gauche de la distribution.

Dans notre exemple précédent, l’asymétrie était positive, ce qui indique que la distribution des valeurs des données était positivement asymétrique ou « à droite ».

Ressources additionnelles

Consultez cet article pour une belle explication des distributions asymétriques à gauche et à droite.