Wprowadzenie do regresji logistycznej

Kiedy chcemy zrozumieć związek między jedną lub większą liczbą zmiennych predykcyjnych a zmienną odpowiedzi ciągłej, często używamy regresji liniowej .

Jeśli jednak zmienna odpowiedzi ma charakter kategoryczny, możemy zastosować regresję logistyczną .

Regresja logistyczna jest rodzajem algorytmu klasyfikacji , ponieważ próbuje „klasyfikować” obserwacje w zbiorze danych na odrębne kategorie.

Oto kilka przykładów zastosowania regresji logistycznej:

• Na podstawie oceny zdolności kredytowej i salda banku chcemy przewidzieć, czy dany klient nie spłaci kredytu. (Zmienna odpowiedzi = „Domyślnie” lub „Brak wartości domyślnej”)
• Chcemy wykorzystać średnią zbiórek na mecz i średnią punktów na mecz , aby przewidzieć, czy dany koszykarz zostanie powołany do NBA (zmienna odpowiedzi = „Draft” lub „Undrafted”).
• Chcemy na podstawie powierzchni kwadratowej i liczby łazienek przewidzieć, czy dom w danym mieście będzie wystawiony za cenę sprzedaży wynoszącą 200 000 USD lub więcej. (Zmienna odpowiedzi = „Tak” lub „Nie”)

Należy zauważyć, że zmienna odpowiedzi w każdym z tych przykładów może przyjmować tylko jedną z dwóch wartości. Porównaj to z regresją liniową, w której zmienna odpowiedzi przyjmuje wartość ciągłą.

Równanie regresji logistycznej

Regresja logistyczna wykorzystuje metodę zwaną estymacją największej wiarygodności (szczegóły nie będą tutaj omawiane), aby znaleźć równanie w następującej postaci:

log[p(X) / ( ₁ -p(X))] = β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p

Złoto:

• X _j : j- ^ta zmienna predykcyjna
• β _j : estymacja współczynnika dla j ^-tej zmiennej predykcyjnej

Wzór po prawej stronie równania przewiduje logarytm szansy , że zmienna odpowiedzi przyjmie wartość 1.

Zatem dopasowując model regresji logistycznej, możemy użyć poniższego równania do obliczenia prawdopodobieństwa, że dana obserwacja przyjmie wartość 1:

p(X) = e ^{β ₀ + β _{1 X 1 + β 2 X 2 + … + β p}}

Następnie używamy pewnego progu prawdopodobieństwa, aby sklasyfikować obserwację jako 1 lub 0.

Na przykład możemy powiedzieć, że obserwacje z prawdopodobieństwem większym lub równym 0,5 zostaną sklasyfikowane jako „1”, a wszystkie inne obserwacje zostaną sklasyfikowane jako „0”.

Jak interpretować wynik regresji logistycznej

Załóżmy, że używamy modelu regresji logistycznej, aby przewidzieć, czy dany koszykarz zostanie powołany do NBA, na podstawie jego średnich zbiórek na mecz i średniej liczby punktów na mecz.

Oto wynik modelu regresji logistycznej:

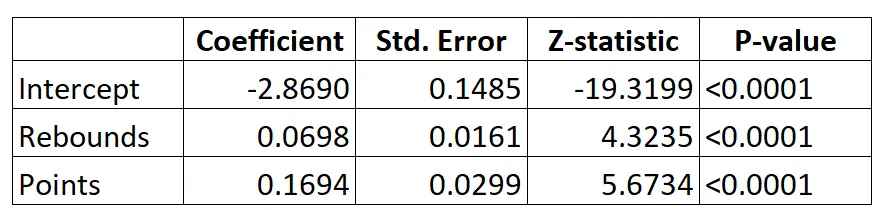
Korzystając ze współczynników, możemy obliczyć prawdopodobieństwo powołania danego zawodnika do NBA na podstawie jego średniej zbiórki i punktów na mecz, korzystając ze wzoru:

P(Wyciąg) = e ^{-2,8690 + 0,0698*(rebs) + 0,1694*(punkty)} / (1+e ^{-2,8690 + 0,0698*(rebs) + 0,1694*(punkty) ) )}

Załóżmy na przykład, że dany zawodnik średnio zdobywa 8 zbiórek na mecz i 15 punktów na mecz. Według modelu prawdopodobieństwo, że ten zawodnik zostanie powołany do NBA wynosi 0,557 .

P(Pisemne) = e ^{-2,8690 + 0,0698*(8) + 0,1694*(15)} / (1+e ^{-2,8690 + 0,0698*(8) + 0,1694*(15 )} ) = 0,557

Ponieważ prawdopodobieństwo to jest większe niż 0,5, przewidujemy, że ten zawodnik zostanie wybrany.

Porównajmy to z zawodnikiem, który średnio zdobywa tylko 3 zbiórki i 7 punktów na mecz. Prawdopodobieństwo, że ten zawodnik zostanie powołany do NBA wynosi 0,186 .

P(Pisemne) = e ^{-2,8690 + 0,0698*(3) + 0,1694*(7)} / (1+e ^{-2,8690 + 0,0698*(3) + 0,1694*(7 )} ) = 0,186

Ponieważ prawdopodobieństwo to jest mniejsze niż 0,5, przewidujemy, że ten zawodnik nie zostanie wybrany.

Założenia regresji logistycznej

Regresja logistyczna wykorzystuje następujące założenia:

1. Zmienna odpowiedzi jest binarna. Zakłada się, że zmienna odpowiedzi może przyjmować tylko dwa możliwe wyniki.

2. Obserwacje są niezależne. Zakłada się, że obserwacje w zbiorze danych są od siebie niezależne. Oznacza to, że obserwacje nie powinny pochodzić z powtarzanych pomiarów tej samej osoby ani być ze sobą w żaden sposób powiązane.

3. Nie ma poważnej współliniowości pomiędzy zmiennymi predykcyjnymi . Zakłada się, że żadna ze zmiennych predykcyjnych nie jest ze sobą silnie skorelowana .

4. Nie ma skrajnych wartości odstających. Zakłada się, że w zbiorze danych nie ma skrajnych wartości odstających ani wpływowych obserwacji.

5. Istnieje liniowa zależność pomiędzy zmiennymi predykcyjnymi a logitem zmiennej odpowiedzi . Hipotezę tę można sprawdzić za pomocą testu Boxa-Tidwella.

6. Wielkość próbki jest wystarczająco duża. Zazwyczaj dla każdej zmiennej objaśniającej powinno być co najmniej 10 przypadków z najrzadziej występującymi wynikami. Na przykład, jeśli masz 3 zmienne objaśniające, a oczekiwane prawdopodobieństwo wystąpienia najrzadszego wyniku wynosi 0,20, wówczas wielkość próby powinna wynosić co najmniej (10*3) / 0,20 = 150.

Sprawdź ten artykuł, aby uzyskać szczegółowe wyjaśnienie, jak zweryfikować te założenia.