Czym jest nadmierne dopasowanie w uczeniu maszynowym? (wyjaśnienie i przykłady)

W uczeniu maszynowym często budujemy modele, dzięki którym możemy dokonywać dokładnych przewidywań dotyczących określonych zjawisk.

Załóżmy na przykład, że chcemy utworzyć model regresji , który wykorzystuje zmienną predykcyjną liczbę godzin spędzonych na nauce do przewidywania wyniku ACT zmiennej odpowiedzi dla uczniów szkół średnich.

Aby zbudować ten model, zbierzemy dane dotyczące godzin spędzonych na nauce i odpowiadającego im wyniku ACT dla setek uczniów w określonym okręgu szkolnym.

Następnie wykorzystamy te dane do wyszkolenia modelu, który może przewidywać wynik, jaki otrzyma dany uczeń, na podstawie całkowitej liczby przestudiowanych godzin.

Aby ocenić przydatność modelu, możemy zmierzyć, jak dobrze przewidywania modelu odpowiadają obserwowanym danym. Jedną z najczęściej używanych w tym celu miar jest błąd średniokwadratowy (MSE), który oblicza się w następujący sposób:

MSE = (1/n)*Σ(y _i – f(x _i )) ²

Złoto:

• n: całkowita liczba obserwacji
• y _i : Wartość odpowiedzi i ^-tej obserwacji
• f(x _i ): Przewidywana wartość odpowiedzi i- ^tej obserwacji

Im bardziej prognozy modelu będą zbliżone do obserwacji, tym niższy będzie MSE.

Jednak jednym z największych błędów popełnianych w uczeniu maszynowym jest optymalizacja modeli w celu zmniejszenia MSE szkoleniowego , czyli tego, jak dobrze przewidywania modelu odpowiadają danym, których użyliśmy do szkolenia modelu.

Kiedy model zbytnio koncentruje się na zmniejszaniu MSE uczącego, często zbyt ciężko pracuje, aby znaleźć wzorce w danych uczących, które są po prostu spowodowane przypadkiem. Następnie, gdy model zostanie zastosowany do niewidocznych danych, jego wydajność jest niska.

Zjawisko to znane jest jako nadmierne dopasowanie . Dzieje się tak, gdy „dopasowujemy” model zbyt blisko danych uczących i w rezultacie budujemy model, który nie jest przydatny do przewidywania nowych danych.

Przykład nadmiernego dopasowania

Aby zrozumieć nadmierne dopasowanie, wróćmy do przykładu tworzenia modelu regresji, który wykorzystuje godziny spędzone na nauce do przewidywania wyniku ACT .

Załóżmy, że zbieramy dane dla 100 uczniów w określonym okręgu szkolnym i tworzymy szybki wykres rozrzutu, aby zwizualizować związek między dwiema zmiennymi:

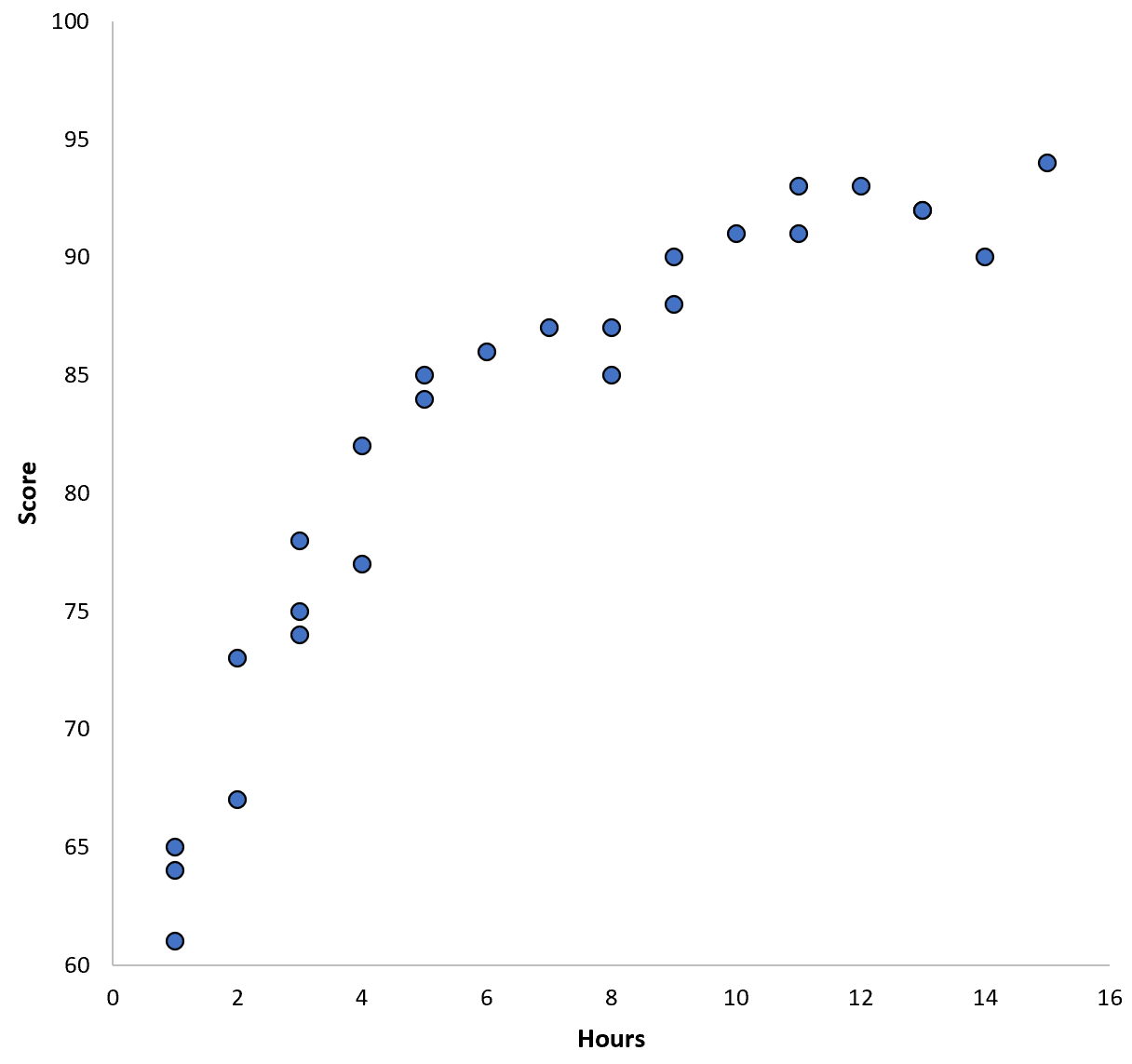
Związek między tymi dwiema zmiennymi wydaje się być kwadratowy, więc załóżmy, że zastosujemy następujący model regresji kwadratowej:

Wynik = 60,1 + 5,4*(godziny) – 0,2*(godziny) ²

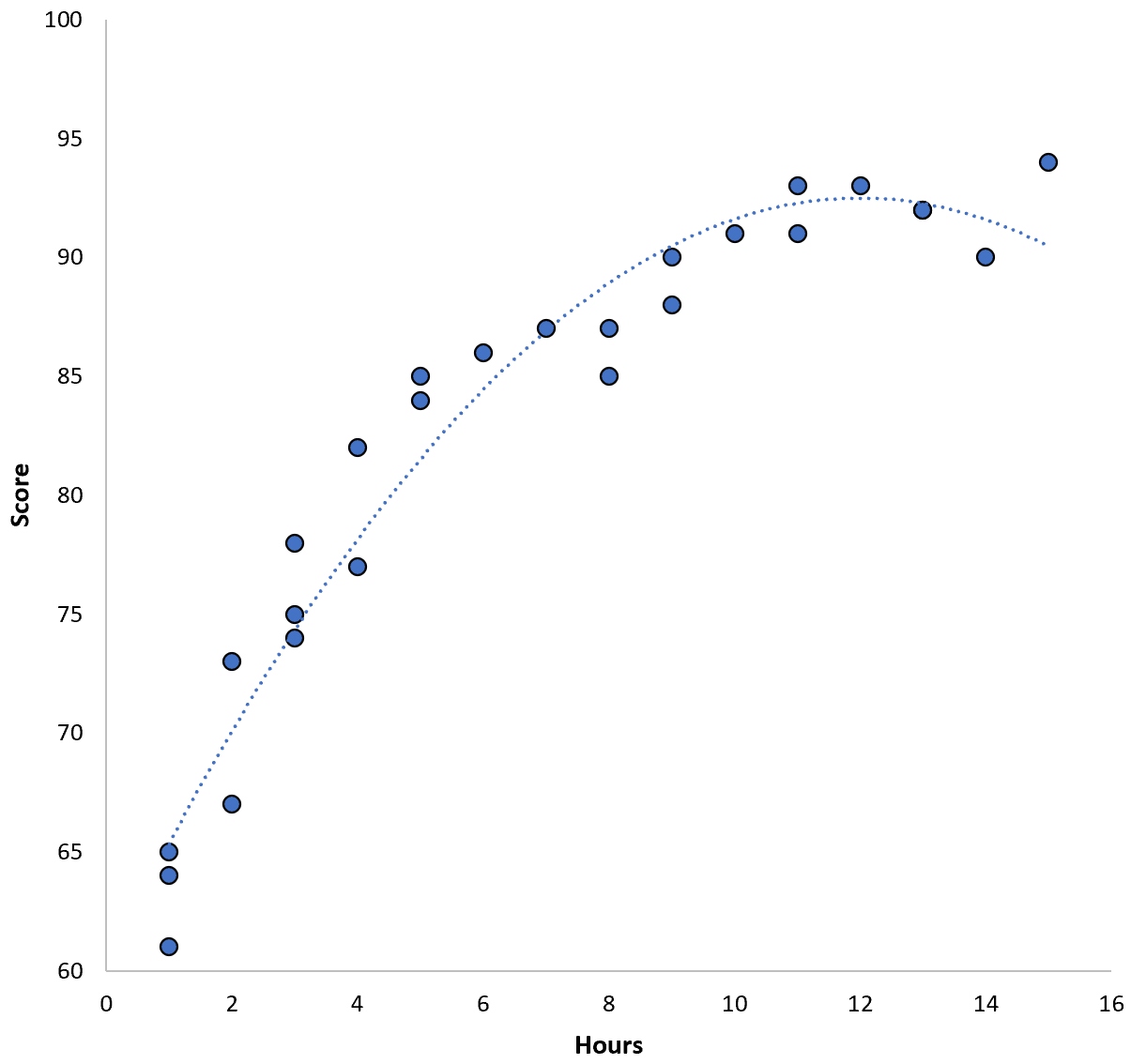
Model ten charakteryzuje się uczącym błędem średniokwadratowym (MSE) wynoszącym 3,45 . Oznacza to, że różnica średniokwadratowa między przewidywaniami dokonanymi przez model a rzeczywistymi wynikami ACT wynosi 3,45.

Moglibyśmy jednak zredukować to szkolenie MSE, dopasowując model wielomianowy wyższego rzędu. Załóżmy na przykład, że zastosujemy następujący model:

Wynik = 64,3 – 7,1*(godziny) + 8,1*(godziny) ² – 2,1*(godziny) ³ + 0,2*(godziny ^{) 4 – 0,1*(godziny) 5 +} 0,2(godziny) ⁶

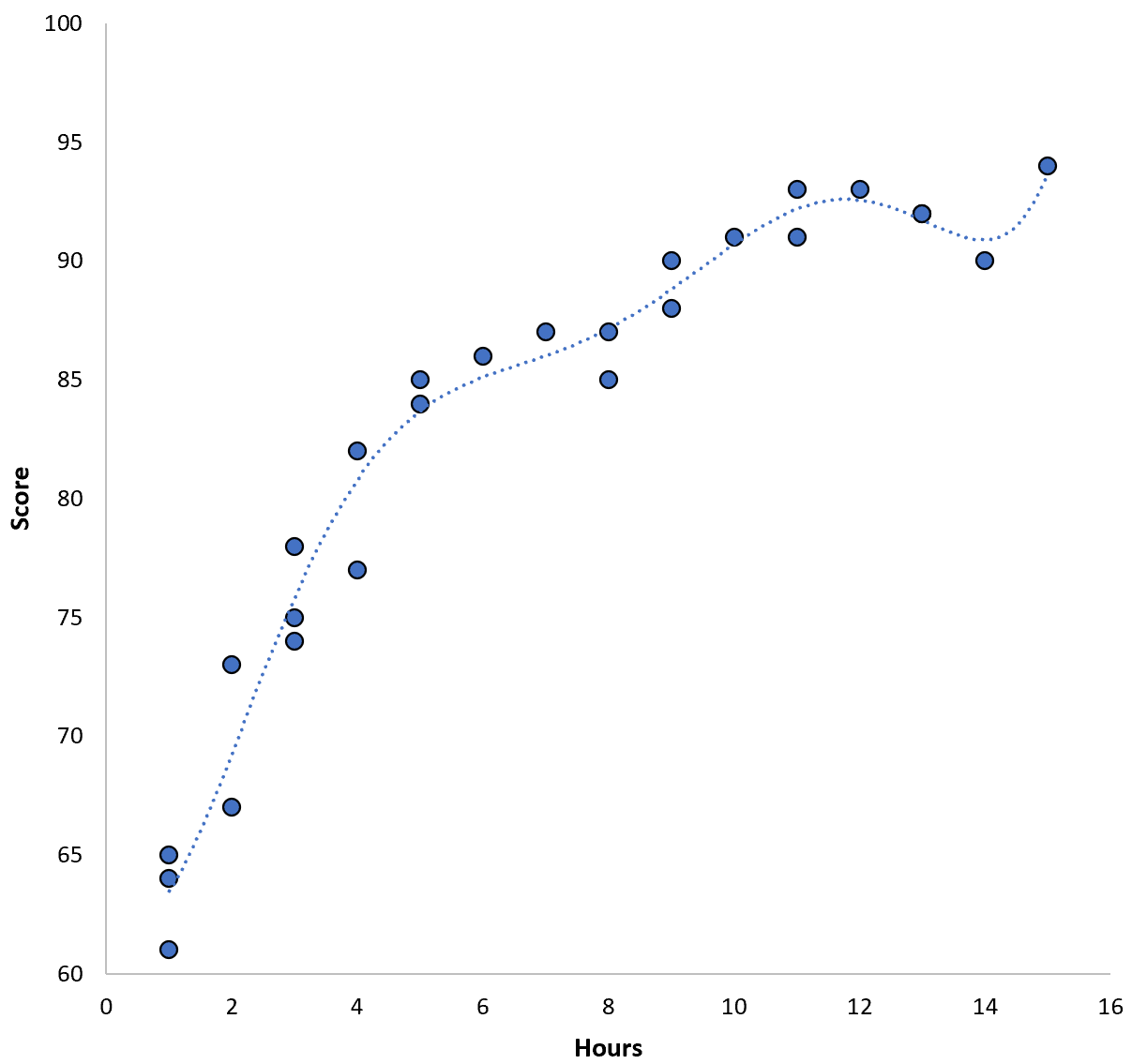
Zwróć uwagę, że linia regresji pasuje do rzeczywistych danych znacznie lepiej niż poprzednia linia regresji.

Model ten ma średni błąd kwadratowy szkolenia (MSE) wynoszący zaledwie 0,89 . Oznacza to, że różnica średniokwadratowa między przewidywaniami dokonanymi przez model a rzeczywistymi wynikami ACT wynosi 0,89.

To szkolenie MSE jest znacznie mniejsze niż szkolenie produkowane przez poprzedni model.

Jednak tak naprawdę nie interesuje nas szkolenie MSE , czyli to, jak dobrze przewidywania modelu odpowiadają danym, których użyliśmy do szkolenia modelu. Zamiast tego interesuje nas głównie test MSE – MSE, gdy nasz model jest stosowany do niewidocznych danych.

Gdybyśmy zastosowali powyższy model regresji wielomianowej wyższego rzędu do niewidocznego zbioru danych, prawdopodobnie działałby on gorzej niż prostszy model regresji kwadratowej. Oznacza to, że spowodowałoby to wyższy wynik testu MSE, a właśnie tego nie chcemy.

Jak wykryć i uniknąć nadmiernego dopasowania

Najprostszym sposobem wykrycia nadmiernego dopasowania jest przeprowadzenie walidacji krzyżowej. Najczęściej stosowaną metodą jest k-krotna walidacja krzyżowa , która działa w następujący sposób:

Krok 1: Losowo podziel zbiór danych na k grup, czyli „fałd”, o mniej więcej równej wielkości.

Krok 2: Wybierz jedną z zakładek jako zestaw do trzymania. Dopasuj szablon do pozostałych zakładek k-1. Oblicz test MSE na podstawie obserwacji w naprężonej warstwie.

Krok 3: Powtórz ten proces k razy, za każdym razem używając innego zbioru jako zbioru wykluczającego.

Krok 4: Oblicz ogólne MSE testu jako średnią k MSE testu.

Test MSE = (1/k)*ΣMSE _tj

Złoto:

• k: Liczba fałd
• MSE _i : Testuje MSE w ^i-tej iteracji

Ten test MSE daje nam dobre wyobrażenie o tym, jak dany model będzie się zachowywał na nieznanych danych.

W praktyce możemy dopasować kilka różnych modeli i przeprowadzić k-krotną weryfikację krzyżową każdego modelu, aby znaleźć jego test MSE. Następnie możemy wybrać model z najniższym testem MSE jako najlepszy model do wykorzystania do prognozowania w przyszłości.

Dzięki temu wybieramy model, który prawdopodobnie będzie najlepiej działał na przyszłych danych, w przeciwieństwie do modelu, który po prostu minimalizuje MSE uczące i „dobrze pasuje” do danych historycznych.

Dodatkowe zasoby

Jaki jest kompromis wariancji odchylenia w uczeniu maszynowym?
Wprowadzenie do walidacji krzyżowej typu K
Modele regresji i klasyfikacji w uczeniu maszynowym