Regresja grzbietu w r (krok po kroku)
Regresja grzbietowa to metoda, której możemy użyć do dopasowania modelu regresji, gdy w danych występuje wieloliniowość .
W skrócie, regresja metodą najmniejszych kwadratów próbuje znaleźć oszacowania współczynników, które minimalizują rezydualną sumę kwadratów (RSS):
RSS = Σ(y i – ŷ i )2
Złoto:
- Σ : Grecki symbol oznaczający sumę
- y i : rzeczywista wartość odpowiedzi dla i-tej obserwacji
- ŷ i : Przewidywana wartość odpowiedzi na podstawie modelu wielokrotnej regresji liniowej
I odwrotnie, regresja grzbietu ma na celu zminimalizowanie następujących elementów:
RSS + λΣβ j 2
gdzie j przechodzi od 1 do p zmiennych predykcyjnych i λ ≥ 0.
Ten drugi człon równania nazywany jest karą za wycofanie . W regresji grzbietowej wybieramy wartość λ, która daje najniższy możliwy test MSE (średni błąd kwadratowy).
W tym samouczku przedstawiono krok po kroku przykład wykonania regresji grzbietu w języku R.
Krok 1: Załaduj dane
W tym przykładzie użyjemy wbudowanego zbioru danych R o nazwie mtcars . Użyjemy hp jako zmiennej odpowiedzi i następujących zmiennych jako predyktorów:
- mpg
- waga
- gówno
- sek
Do wykonania regresji grzbietowej wykorzystamy funkcje z pakietu glmnet . Pakiet ten wymaga, aby zmienna odpowiedzi była wektorem, a zestaw zmiennych predykcyjnych był klasy data.matrix .
Poniższy kod pokazuje jak zdefiniować nasze dane:
#define response variable
y <- mtcars$hp
#define matrix of predictor variables
x <- data.matrix(mtcars[, c('mpg', 'wt', 'drat', 'qsec')])
Krok 2: Dopasuj model regresji grzbietu
Następnie użyjemy funkcji glmnet() , aby dopasować model regresji Ridge’a i określić alfa=0 .
Należy pamiętać, że ustawienie alfa równego 1 jest równoznaczne z użyciem regresji Lasso, a ustawienie alfa na wartość z zakresu od 0 do 1 jest równoznaczne z użyciem elastycznej siatki.
Należy również pamiętać, że regresja grzbietowa wymaga standaryzacji danych w taki sposób, aby każda zmienna predykcyjna miała średnią 0 i odchylenie standardowe 1.
Na szczęście glmnet() automatycznie wykonuje tę standaryzację za Ciebie. Jeśli już znormalizowałeś zmienne, możesz określić standize=False .
library (glmnet)
#fit ridge regression model
model <- glmnet(x, y, alpha = 0 )
#view summary of model
summary(model)
Length Class Mode
a0 100 -none- numeric
beta 400 dgCMatrix S4
df 100 -none- numeric
dim 2 -none- numeric
lambda 100 -none- numeric
dev.ratio 100 -none- numeric
nulldev 1 -none- numeric
npasses 1 -none- numeric
jerr 1 -none- numeric
offset 1 -none- logical
call 4 -none- call
nobs 1 -none- numeric
Krok 3: Wybierz optymalną wartość Lambdy
Następnie zidentyfikujemy wartość lambda, która daje najniższy średni błąd kwadratowy testu (MSE), stosując k-krotną walidację krzyżową .
Na szczęście glmnet ma funkcję cv.glmnet() , która automatycznie wykonuje k-krotną weryfikację krzyżową przy użyciu k = 10 razy.
#perform k-fold cross-validation to find optimal lambda value
cv_model <- cv. glmnet (x, y, alpha = 0 )
#find optimal lambda value that minimizes test MSE
best_lambda <- cv_model$ lambda . min
best_lambda
[1] 10.04567
#produce plot of test MSE by lambda value
plot(cv_model)
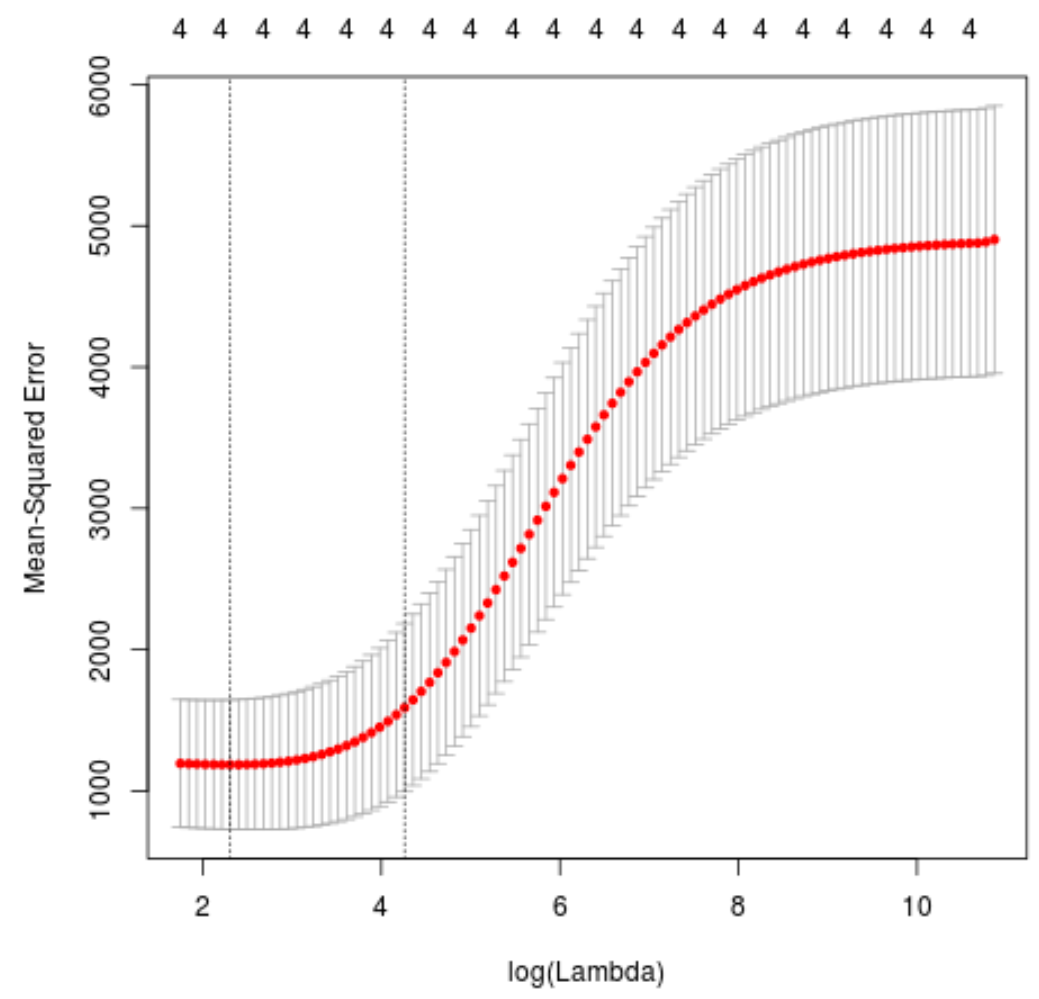
Wartość lambda minimalizująca test MSE okazuje się wynosić 10,04567 .
Krok 4: Przeanalizuj ostateczny model
Na koniec możemy przeanalizować ostateczny model uzyskany na podstawie optymalnej wartości lambda.
Aby uzyskać estymatory współczynników dla tego modelu, możemy użyć następującego kodu:
#find coefficients of best model
best_model <- glmnet(x, y, alpha = 0 , lambda = best_lambda)
coef(best_model)
5 x 1 sparse Matrix of class "dgCMatrix"
s0
(Intercept) 475.242646
mpg -3.299732
wt 19.431238
drat -1.222429
qsec -17.949721
Możemy również utworzyć wykres śledzenia, aby zwizualizować, jak zmieniły się szacunki współczynników ze względu na wzrost lambda:
#produce Ridge trace plot
plot(model, xvar = " lambda ")
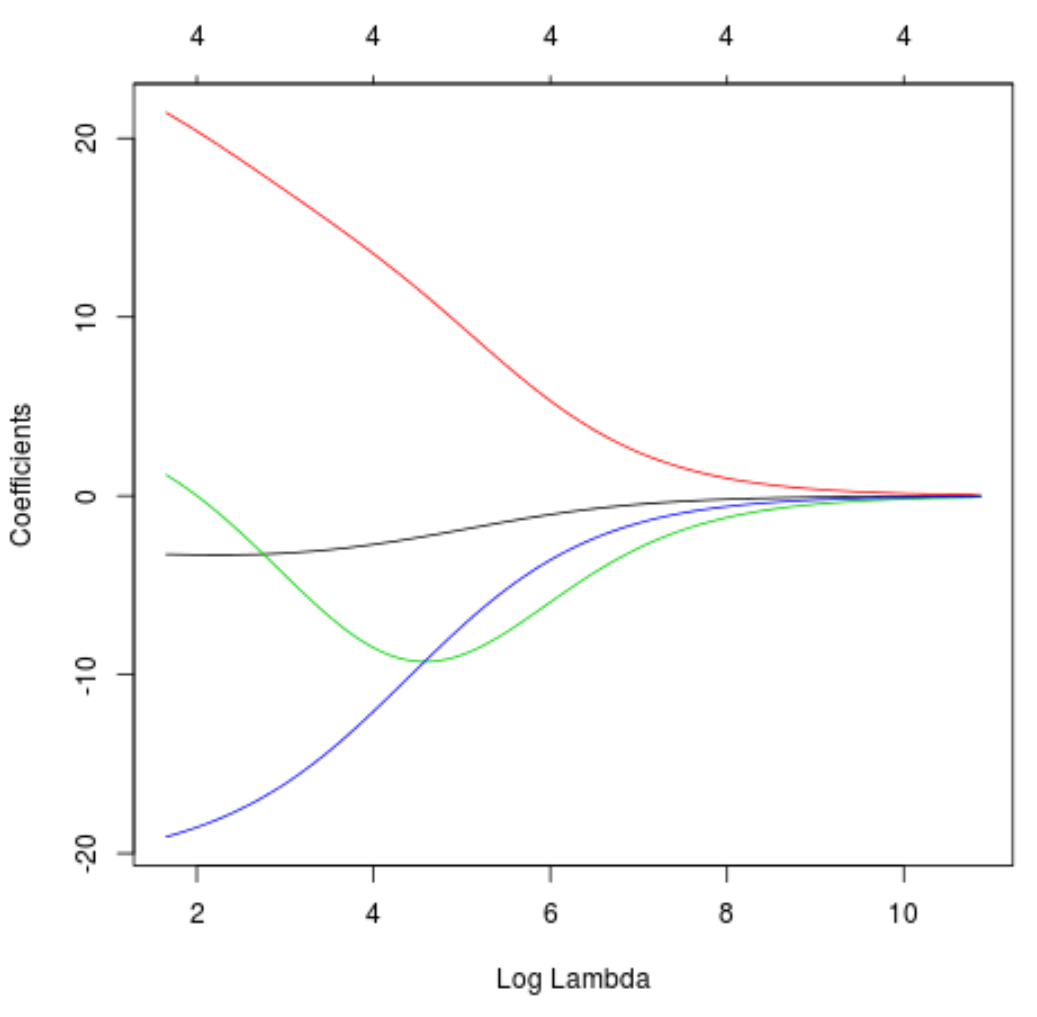
Na koniec możemy obliczyć R-kwadrat modelu na danych treningowych:
#use fitted best model to make predictions
y_predicted <- predict (model, s = best_lambda, newx = x)
#find OHS and SSE
sst <- sum ((y - mean (y))^2)
sse <- sum ((y_predicted - y)^2)
#find R-Squared
rsq <- 1 - sse/sst
rsq
[1] 0.7999513
Okazuje się, że R kwadrat wynosi 0,7999513 . Oznacza to, że najlepszy model był w stanie wyjaśnić 79,99% zmienności wartości odpowiedzi danych treningowych.
Pełny kod R użyty w tym przykładzie znajdziesz tutaj .