Kiedy stosować regresję grzbietu i lasso

W zwykłej wielokrotnej regresji liniowej używamy zestawu p zmiennych predykcyjnych i zmiennej odpowiedzi, aby dopasować model w postaci:

Y = β ₀ + β ₁ X _{1 +} β ₂ X ₂ + … + β _p

Wartości β ₀ , β ₁ , B ₂ , …, β _p dobieramy metodą najmniejszych kwadratów, która minimalizuje sumę kwadratów reszt (RSS):

RSS = Σ(y _i – ŷ _i ) ²

Złoto:

• Σ : Symbol oznaczający „sumę”
• y _i : rzeczywista wartość odpowiedzi dla ^i-tej obserwacji
• ŷ _i : Przewidywana wartość odpowiedzi dla i- ^tej obserwacji

Problem wielowspółliniowości w regresji

Problemem, który często pojawia się w praktyce w przypadku wielokrotnej regresji liniowej, jest wieloliniowość – gdy dwie lub więcej zmiennych predykcyjnych jest ze sobą silnie skorelowanych, tak że nie dostarczają unikalnych lub niezależnych informacji w modelu regresji.

Może to sprawić, że szacunki współczynników modelu będą niewiarygodne i będą wykazywać dużą wariancję. Oznacza to, że gdy model zostanie zastosowany do nowego zbioru danych, którego nigdy wcześniej nie widział, prawdopodobnie będzie działał słabo.

Unikanie współliniowości: regresja Ridge’a i Lasso

Dwie metody, których możemy użyć, aby obejść ten problem współliniowości, to regresja grzbietowa i regresja lassa .

Regresja grzbietowa ma na celu zminimalizowanie następujących elementów:

• RSS + λΣβ _j ²

Regresja Lasso ma na celu zminimalizowanie następujących elementów:

• RSS + λΣ|β _j |

W obu równaniach drugi człon nazywany jest karą za wycofanie .

Gdy λ = 0, ten składnik kary nie ma żadnego efektu, a regresja grzbietowa i regresja lasso dają takie same szacunki współczynników, jak metoda najmniejszych kwadratów.

Jednakże, gdy λ zbliża się do nieskończoności, kara za skurcz staje się bardziej wpływowa, a zmienne predykcyjne, których nie można zaimportować do modelu, zmniejszają się do zera.

Dzięki regresji Lasso niektóre współczynniki mogą osiągnąć całkowite zero , gdy λ stanie się wystarczająco duże.

Zalety i wady regresji Ridge’a i Lasso

Przewagą regresji Ridge’a i Lasso nad regresją metodą najmniejszych kwadratów jest kompromis w zakresie odchylenia i wariancji .

Przypomnijmy, że błąd średniokwadratowy (MSE) to metryka, za pomocą której możemy zmierzyć dokładność danego modelu i oblicza się go w następujący sposób:

MSE = Var( f̂( x ₀ )) + [Odchylenie( f̂( x ₀ ))] ² + Var(ε)

MSE = wariancja + błąd ² + błąd nieredukowalny

Podstawową ideą regresji grzbietowej i regresji lasso jest wprowadzenie małego błędu systematycznego, dzięki czemu wariancja może zostać znacznie zmniejszona, co prowadzi do niższego ogólnego MSE.

Aby to zilustrować, rozważ następujący wykres:

Należy zauważyć, że wraz ze wzrostem λ wariancja znacznie maleje przy bardzo małym wzroście obciążenia. Jednak powyżej pewnego punktu wariancja maleje wolniej, a spadek współczynników prowadzi do ich znacznego niedoszacowania, co prowadzi do gwałtownego wzrostu obciążenia systematycznego.

Z wykresu widzimy, że MSE testu jest najniższe, gdy wybierzemy wartość λ, która zapewnia optymalny kompromis między obciążeniem a wariancją.

Gdy λ = 0, składnik karny w regresji lasso nie ma żadnego efektu i dlatego daje takie same oszacowania współczynników, jak metoda najmniejszych kwadratów. Jednakże, zwiększając λ do pewnego punktu, możemy zmniejszyć całkowite MSE testu.

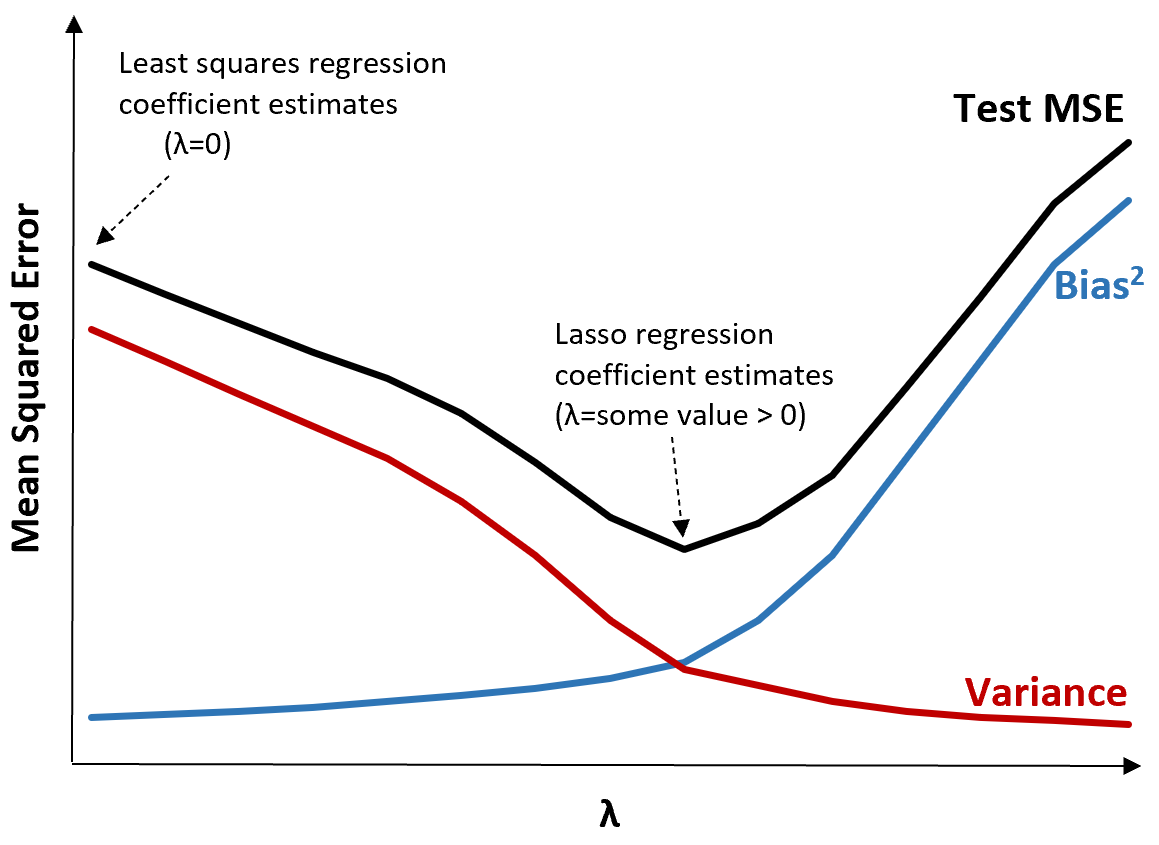
Oznacza to, że dopasowanie modelu za pomocą regresji grzbietowej i lassa może potencjalnie powodować mniejsze błędy testowe niż dopasowanie modelu za pomocą regresji najmniejszych kwadratów.

Wadą regresji Ridge’a i Lasso jest to, że interpretacja współczynników w ostatecznym modelu staje się trudna, gdy zmniejszają się one do zera.

Zatem regresję Ridge’a i Lasso należy stosować, jeśli chcesz zoptymalizować zdolność przewidywania, a nie wnioskowanie.

Ridge kontra Regresja Lasso: kiedy używać każdego z nich

Regresja Lasso i regresja grzbietowa są znane jako metody regularyzacji , ponieważ obie mają na celu zminimalizowanie resztowej sumy kwadratów (RSS), a także określonego warunku kary.

Innymi słowy, ograniczają lub regulują oszacowania współczynników modelu.

To naturalnie rodzi pytanie: czy lepsza jest regresja grzbietu czy lassa?

W przypadkach, gdy istotna jest tylko niewielka liczba zmiennych predykcyjnych, regresja lasso zwykle działa lepiej, ponieważ jest w stanie całkowicie zredukować nieistotne zmienne do zera i usunąć je z modelu.

Jednakże, gdy w modelu znaczących jest wiele zmiennych predykcyjnych, a ich współczynniki są w przybliżeniu równe, regresja grzbietowa zwykle działa lepiej, ponieważ utrzymuje wszystkie predyktory w modelu.

Aby określić, który model jest najlepszy do prognozowania, zazwyczaj przeprowadzamy k-krotną weryfikację krzyżową i wybieramy model, który daje najniższy średni błąd kwadratowy testu.

Dodatkowe zasoby

Poniższe samouczki stanowią wprowadzenie do regresji grzbietowej i regresji lasso:

• Wprowadzenie do regresji grzbietu
• Wprowadzenie do regresji Lasso

Poniższe samouczki wyjaśniają, jak przeprowadzić oba typy regresji w R i Pythonie:

• Regresja grzbietu w R
• Regresja grzbietu w Pythonie
• Regresja Lasso w R
• Regresja Lasso w Pythonie