Twierdzenie bayesa

W tym artykule wyjaśniono, czym jest twierdzenie Bayesa i do czego jest wykorzystywane w prawdopodobieństwie i statystyce. W ten sposób dowiesz się, jaki jest wzór twierdzenia Bayesa, rozwiązane przykłady twierdzenia Bayesa i jakie są zastosowania tego twierdzenia.

Jakie jest twierdzenie Bayesa?

W teorii prawdopodobieństwa twierdzenie Bayesa jest prawem używanym do obliczania prawdopodobieństwa zdarzenia, gdy znana jest a priori informacja o tym zdarzeniu.

Mówiąc dokładniej, twierdzenie Bayesa matematycznie wiąże prawdopodobieństwo zdarzenia A przy danym zdarzeniu B z prawdopodobieństwem B przy danym A.

Na przykład, jeśli znasz z góry prawdopodobieństwo, że dana osoba będzie miała ból głowy w przypadku grypy, możesz użyć twierdzenia Bayesa, aby określić prawdopodobieństwo, że dana osoba będzie miała grypę w przypadku bólu głowy.

Twierdzenie Bayesa ma wiele zastosowań, np. wykorzystuje się je w medycynie, ekonomii czy technologii do obliczania prawdopodobieństw pewnych zdarzeń uwarunkowanych innymi zdarzeniami. Poniżej omówimy szczegółowo różne zastosowania twierdzenia Bayesa.

Twierdzenie Bayesa zostało wymyślone przez angielskiego matematyka Thomasa Bayesa (1702-1761), chociaż zostało opublikowane pośmiertnie w 1763 roku.

Wzór twierdzenia Bayesa

Twierdzenie Bayesa mówi, że mając przestrzeń próbki złożoną ze zbioru wzajemnie wykluczających się zdarzeń {A ₁ , A ₂ ,…, A _i ,…, _An }, których prawdopodobieństwa nie są równe zero, oraz innego zdarzenia B , możemy matematycznie powiązać warunek prawdopodobieństwo A _i, biorąc pod uwagę zdarzenie B, z prawdopodobieństwem warunkowym B, biorąc pod uwagę A _i .

Zatem wzór na twierdzenie Bayesa , znane również jako reguła Bayesa , wygląda następująco:

Złoto:

• 

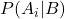
  jest prawdopodobieństwem warunkowym zdarzenia A _{w przypadku} danego zdarzenia B, zwanym prawdopodobieństwem późniejszym.

• 

  jest prawdopodobieństwem warunkowym zdarzenia B przy danym zdarzeniu A _i .

• 

  jest prawdopodobieństwem zajścia zdarzenia A _i , zwanym prawdopodobieństwem apriorycznym.

Należy zauważyć, że mianownikiem wzoru twierdzenia Bayesa jest całkowite prawdopodobieństwo zdarzenia B.

Przykład twierdzenia Bayesa

Kiedy już poznamy definicję twierdzenia Bayesa i jego wzór, zobaczymy rozwiązany przykład obliczania prawdopodobieństwa za pomocą twierdzenia Bayesa, aby lepiej zrozumieć tę koncepcję.

• W sklepie z elektroniką znajdują się telewizory trzech marek: X, Y, Z. Szacuje się, że 20% sprzedaży stanowią telewizory marki Y są wadliwe, 3% telewizory marki Y są wadliwe, a 4% telewizory marki Z są wadliwe. Jakie jest prawdopodobieństwo, że jest to telewizor marki Z, biorąc pod uwagę wadliwy telewizor?

Ćwiczenie daje nam prawdopodobieństwo, że klient kupi telewizor każdej marki:

• Zdarzenie A ₁ : Klient kupuje telewizor marki X → P(A ₁ )=0,20
• Zdarzenie A ₂ : Klient kupuje telewizor marki Y → P(A ₂ )=0,50
• Zdarzenie A ₃ : Klient kupuje telewizor marki Z → P(A ₃ )=0,30

Ponadto odczyt daje nam również prawdopodobieństwo, że telewizor każdej marki jest uszkodzony:

Zdarzenie B: Telewizor jest uszkodzony

• B|A ₁ : Telewizor marki X jest uszkodzony → P(B|A ₁ )=0,05
• B|A ₂ : Telewizor marki Y jest uszkodzony → P(B|A ₂ )=0,03
• B|A ₃ : Telewizor marki Z jest uszkodzony → P(B|A ₃ )=0,04

Zatem drzewo prawdopodobieństwa wszystkich interesujących nas zdarzeń wygląda następująco:

Aby więc obliczyć prawdopodobieństwo, że w przypadku uszkodzonego telewizora będzie to telewizor marki Z, musimy skorzystać ze wzoru z twierdzenia Bayesa:

Używając terminologii użytej w tym przykładzie, wzór Bayesa wygląda następująco:

Zatem obliczenie prawdopodobieństwa, że dany wadliwy telewizor to marka Z, wygląda następująco:

Podsumowując, prawdopodobieństwo, że jeśli telewizor jest uszkodzony, jest to marka Z, wynosi 32%.

Zastosowania twierdzenia Bayesa

Twierdzenie Bayesa ma wiele zastosowań, w tym:

1. Testy medyczne : Twierdzenie Bayesa jest często stosowane w medycynie do określenia prawdopodobieństwa przejścia testów diagnostycznych. Na przykład w przypadku testu na obecność wirusa HIV twierdzenie to można wykorzystać do obliczenia prawdopodobieństwa, że dana osoba faktycznie jest zakażona wirusem, jeśli wynik testu jest pozytywny.
2. Analiza finansowa : W finansach twierdzenie Bayesa służy do obliczania prawdopodobieństwa wystąpienia określonych zdarzeń gospodarczych, takich jak wzrost lub spadek wartości akcji, przy założeniu zestawu zmiennych ekonomicznych.
3. Badania rynku : Twierdzenie Bayesa pozwala na określenie np. prawdopodobieństwa, że dana osoba kupi produkt po zobaczeniu reklamy tego produktu.
4. Prognozowanie pogody : Modele pogody wykorzystują również twierdzenie Bayesa do określenia prawdopodobieństwa spełnienia się danej prognozy pogody na podstawie zaobserwowanych danych. Poprawia to dokładność prognoz klimatycznych.
5. Bezpieczeństwo komputerowe – w cyberbezpieczeństwie twierdzenie Bayesa można zastosować do określenia prawdopodobieństwa, że podejrzane działanie jest w rzeczywistości atakiem na system komputerowy.

Rozwiązane problemy z twierdzeniem Bayesa

Ćwiczenie 1

Szacuje się, że na jakąś chorobę cierpi 1% populacji. Test wykrywający tę chorobę ma skuteczność w 95% w przypadku przypadków pozytywnych i 90% w przypadku przypadków negatywnych. Jeśli losowo wybrana osoba uzyska wynik pozytywny, jakie jest prawdopodobieństwo, że rzeczywiście jest ona chora?

Instrukcja ćwiczenia daje nam następujące prawdopodobieństwa:

A ₁ : Osoba jest chora → P(A ₁ )=0,01
A ₂ : Osoba nie jest chora → P(A ₂ )=0,99

B: Test jest pozytywny
B|A ₁ : Wynik pozytywny, gdy dana osoba jest chora → P(B|A ₁ )=0,95
B|A ₂ : Test jest pozytywny, gdy dana osoba nie jest chora → P(B|A ₂ )=1-0,90=0,10

Następnie, aby obliczyć prawdopodobieństwo, że losowo wybrana osoba rzeczywiście będzie chora, gdy wynik testu będzie pozytywny, należy zastosować regułę Bayesa:

Podstawiamy więc wartości do wzoru i wykonujemy obliczenie prawdopodobieństwa:

Krótko mówiąc, prawdopodobieństwo, że losowo wybrana osoba uzyska pozytywny wynik testu i rzeczywiście będzie chora, wynosi 8,76%.

Ćwiczenie 2

Szacuje się, że prawdopodobieństwo, że cena akcji w ciągu jednego dnia wzrośnie wynosi 40%, że pozostanie stabilna, wynosi 10%, a że spadnie, wynosi 50%. Co więcej, wiemy, że gdy rynek rośnie, prawdopodobieństwo, że analityk finansowy przewidzi to poprawnie, wynosi 90%, że gdy rynek pozostaje stabilny, prawdopodobieństwo, że prognoza się sprawdzi, wynosi 75%, a w przypadku spadku prawdopodobieństwo trafnej prognozy wynosi 75%. 85%.%. Jeśli analityk przewiduje, że rynek spadnie, jakie jest prawdopodobieństwo, że faktycznie spadnie?

W tym przypadku instrukcja ćwiczenia zapewnia nam następujące prawdopodobieństwa:

A ₁ : Rynek rośnie w ciągu jednego dnia → P(A ₁ )=0,40
A ₂ : Rynek pozostaje stabilny przez jeden dzień → P(A ₂ )=0,10
A ₃ : Rynek rośnie w ciągu jednego dnia → P(A ₃ )=0,50

B: Analityk przewiduje, że rynek spadnie
B|A ₁ : Analityk poprawnie przewiduje, że rynek wzrośnie → P(B|A ₁ )=0,90
B|A ₂ : Analityk poprawnie przewiduje, że rynek pozostanie stabilny → P(B|A ₂ )=0,75
B|A ₃ : Analityk poprawnie przewiduje spadek rynku → P(B|A ₃ )=0,85

Aby określić prawdopodobieństwo, że analityk przewiduje spadek rynku i że jest to prawidłowe, musimy skorzystać ze wzoru twierdzenia Bayesa:

Podstawiamy wartości prawdopodobieństwa do wzoru Bayesa i obliczamy prawdopodobieństwo:

Zatem prawdopodobieństwo, że analityk ma rację mówiąc, że giełda spadnie, wynosi 49,42%.