Schemat drzewa

W tym artykule wyjaśniono, czym jest diagram drzewa i jak jest wykonany. W ten sposób znajdziesz przykłady struktur drzewiastych, zalety tego typu diagramów, a dodatkowo ćwiczenie rozwiązane krok po kroku.

Co to jest drzewo?

Diagram drzewa , zwany także drzewem prawdopodobieństwa , to graficzne przedstawienie wszystkich możliwych wyników eksperymentu wraz z ich prawdopodobieństwami.

Zatem diagram drzewa służy do wykreślenia wszystkich możliwych wyników w przestrzeni próbki i obliczenia ich prawdopodobieństw.

Diagram drzewa jest tworzony w taki sposób, że każdy wynik ( węzeł ) rozgałęzia się na nowe możliwe wyniki ( gałęzie ), aż do osiągnięcia wyników końcowych.

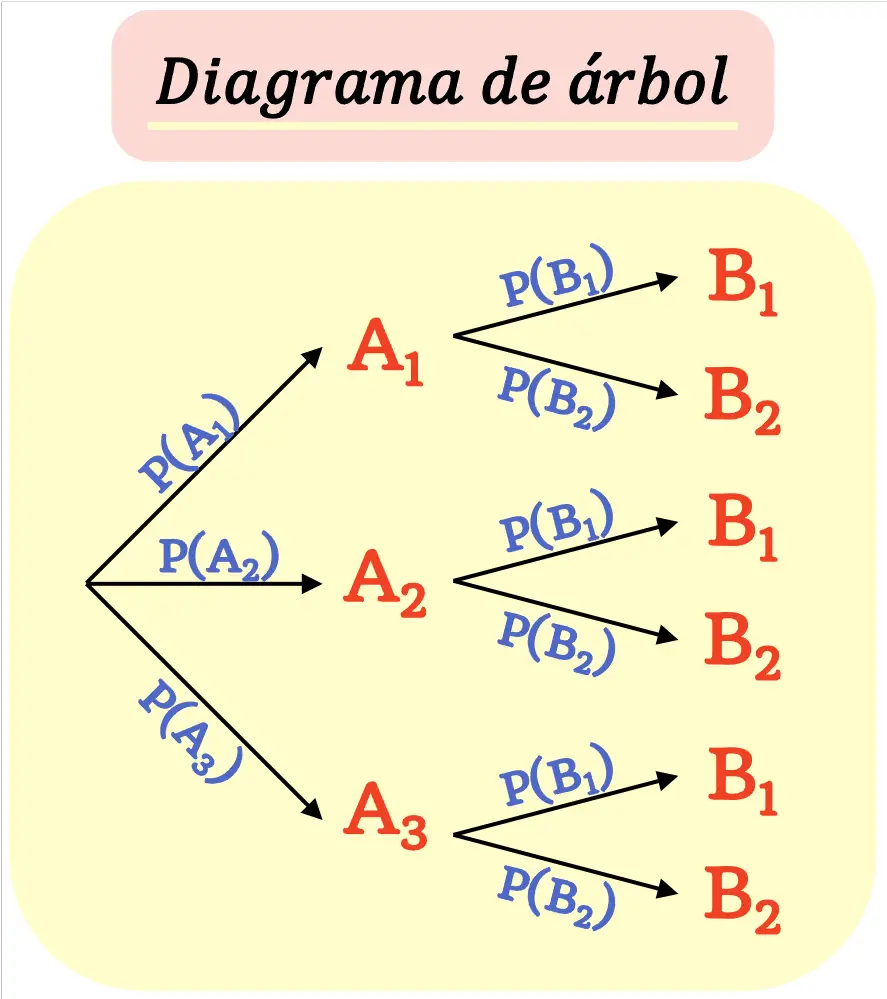
Należy pamiętać, że suma prawdopodobieństw wszystkich gałęzi wychodzących z węzła musi być równa 1.

Jak zrobić diagram drzewa

Aby utworzyć drzewo, wykonaj następujące kroki:

1. Pierwszym krokiem w tworzeniu diagramu drzewa jest narysowanie gałęzi dla każdego możliwego wyniku. Będą to gałęzie pierwszej generacji.
2. Następnie prawdopodobieństwo związane z każdym zdarzeniem jest dodawane do odpowiedniej gałęzi.
3. Koniec każdej gałęzi pierwszej generacji jest węzłem, z którego muszą być reprezentowane gałęzie kolejnych możliwych zdarzeń.
4. Podobnie jak w pierwszych gałęziach, musimy dodać prawdopodobieństwa przedstawionych zdarzeń.
5. Powtarzaj kroki 3 i 4, aż dotrzesz do końcowych węzłów, czyli możliwych zakończeń eksperymentu.

Należy pamiętać, że liczba oddziałów na jednym poziomie nie musi koniecznie być równa liczbie oddziałów na innym poziomie. Podobnie liczba gałęzi wynikających z możliwego wyniku może się różnić nawet w obrębie tego samego poziomu.

Przykład drzewa

Teraz, gdy znamy już definicję i teorię tworzenia diagramu drzewa, przyjrzyjmy się krok po kroku przykładowi z życia wziętego, aby lepiej zrozumieć tę koncepcję.

• Skonstruuj drzewo prawdopodobieństwa rzutu trzema niezależnymi monetami. Następnie określ prawdopodobieństwo uzyskania orła we wszystkich trzech rzutach.

Podczas losowania możliwe są tylko dwa wyniki, możemy otrzymać orzeł lub reszkę. Zatem prawdopodobieństwo wyrzucenia orła lub reszki podczas rzucania monetą wynosi:

Kiedy już znamy prawdopodobieństwa możliwych wyników, przystępujemy do przedstawienia diagramu drzewa.

Ponieważ rzuty monetą są niezależne, prawdopodobieństwo wyrzucenia orła lub reszki będzie zawsze takie samo w każdym rzucie. Dlatego, aby zbudować drzewo, dwie gałęzie (głowa i reszka) muszą być reprezentowane z takim samym prawdopodobieństwem dla każdego wykonanego rzutu.

A kiedy już ułożymy drzewo, jedyne, co musimy zrobić, to określić prawdopodobieństwo uzyskania trzech rzutów monetą.

Dlatego w tym przypadku musimy pomnożyć wszystkie prawdopodobieństwa otrzymania orła, ponieważ są to prawdopodobieństwa ścieżki, która prowadzi nas do pożądanego rezultatu.

Zatem prawdopodobieństwo wyrzucenia orła w trzech rzutach monetą oblicza się w następujący sposób:

Krótko mówiąc, prawdopodobieństwo wyrzucenia orła trzy razy z rzędu wynosi 12,5%.

Rozwiązane ćwiczenie drzewa

Na wsi są tylko 3 żłobki: 60% dzieci uczęszcza do żłobka A, 30% do żłobka B i 10% do żłobka C. Ponadto w trzech żłobkach 55% stanowią dziewczynki. Zbuduj drzewo i oblicz następujące prawdopodobieństwa:

• Prawdopodobieństwo, że w przypadku losowego wyboru dziecka będzie to dziewczynka z przedszkola B.
• Prawdopodobieństwo, że losowo wybrane dziecko z dowolnego przedszkola będzie chłopcem.

Należy pamiętać, że jeśli odsetek dziewcząt we wszystkich przedszkolach wynosi 55%, odsetek chłopców oblicza się po prostu odejmując 1 minus 0,55:

Teraz, gdy znamy już wszystkie prawdopodobieństwa, możemy stworzyć drzewo prawdopodobieństwa ze wszystkimi możliwościami:

Zatem prawdopodobieństwo losowego wybrania dziewczynki z przedszkola B oblicza się w następujący sposób:

Z drugiej strony, aby określić prawdopodobieństwo wybrania chłopca do dowolnego przedszkola, musimy najpierw znaleźć prawdopodobieństwo wybrania chłopca do każdego przedszkola, a następnie dodać je do siebie:

Zalety struktury drzewiastej

Ze względu na charakterystykę struktury drzewiastej zalety tego typu wykresu statystycznego są następujące:

• Diagramy drzew są bardzo przydatne przy podejmowaniu decyzji.
• Zależność pomiędzy wszystkimi możliwymi wynikami można przedstawić graficznie.
• Znalezienie pierwotnej przyczyny problemu jest bardzo wygodne.
• Ułatwia rozwiązywanie problemów prawdopodobieństwa i statystyki.
• Diagram drzewa pomaga organizować pomysły i analizować sytuację.