Jak przeprowadzić regresję logistyczną w spss

Regresja logistyczna to metoda, której używamy do dopasowania modelu regresji , gdy zmienna odpowiedzi jest binarna.

W tym samouczku wyjaśniono, jak przeprowadzić regresję logistyczną w SPSS.

Przykład: regresja logistyczna w SPSS

Wykonaj poniższe kroki, aby przeprowadzić regresję logistyczną w SPSS dla zbioru danych wskazujących, czy koszykarze z college’u zostali powołani do NBA (draft: 0 = nie, 1 = tak) na podstawie ich GPA. punktów na mecz i poziom ich dywizji.

Krok 1: Wprowadź dane.

Najpierw wprowadź następujące dane:

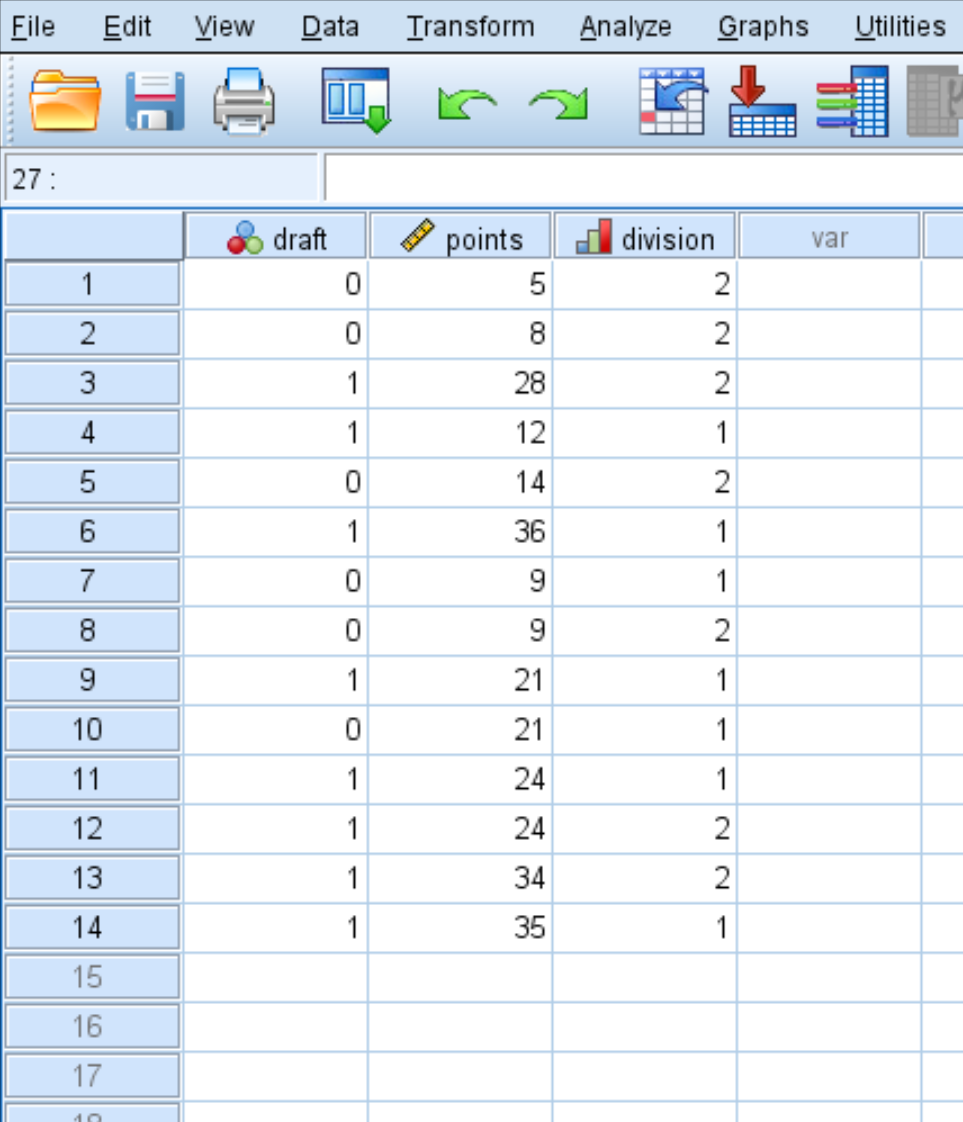
Krok 2: Wykonaj regresję logistyczną.

Kliknij zakładkę Analizuj , następnie Regresja , a następnie Binarna Regresja Logistyczna :

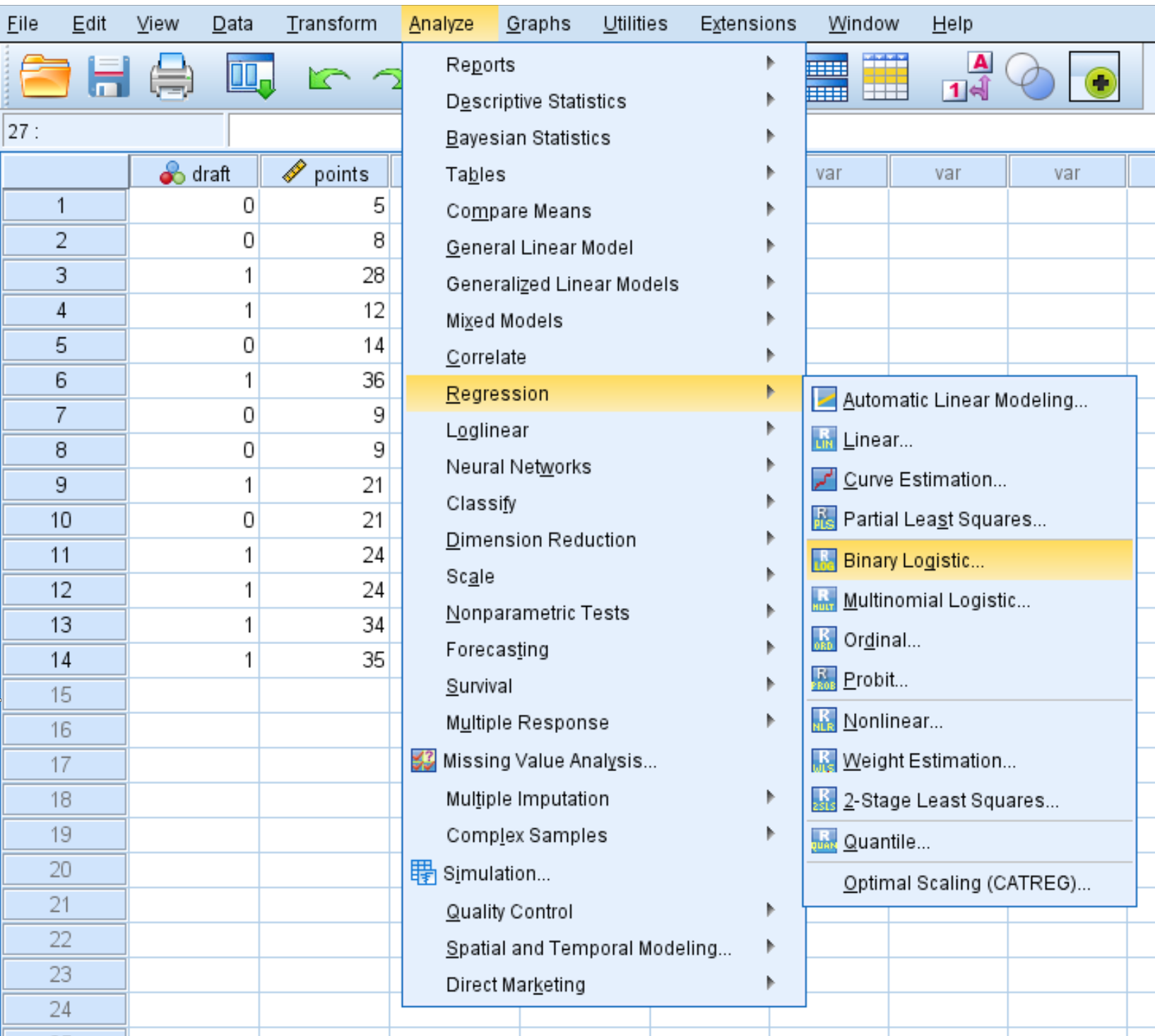
W nowym oknie, które się pojawi, przeciągnij projekt binarnej zmiennej odpowiedzi do obszaru oznaczonego Zależne. Następnie przeciągnij dwukropek i podział zmiennych predykcyjnych do pola oznaczonego Blok 1 z 1. Pozostaw metodę ustawioną na Enter. Następnie kliknij OK .

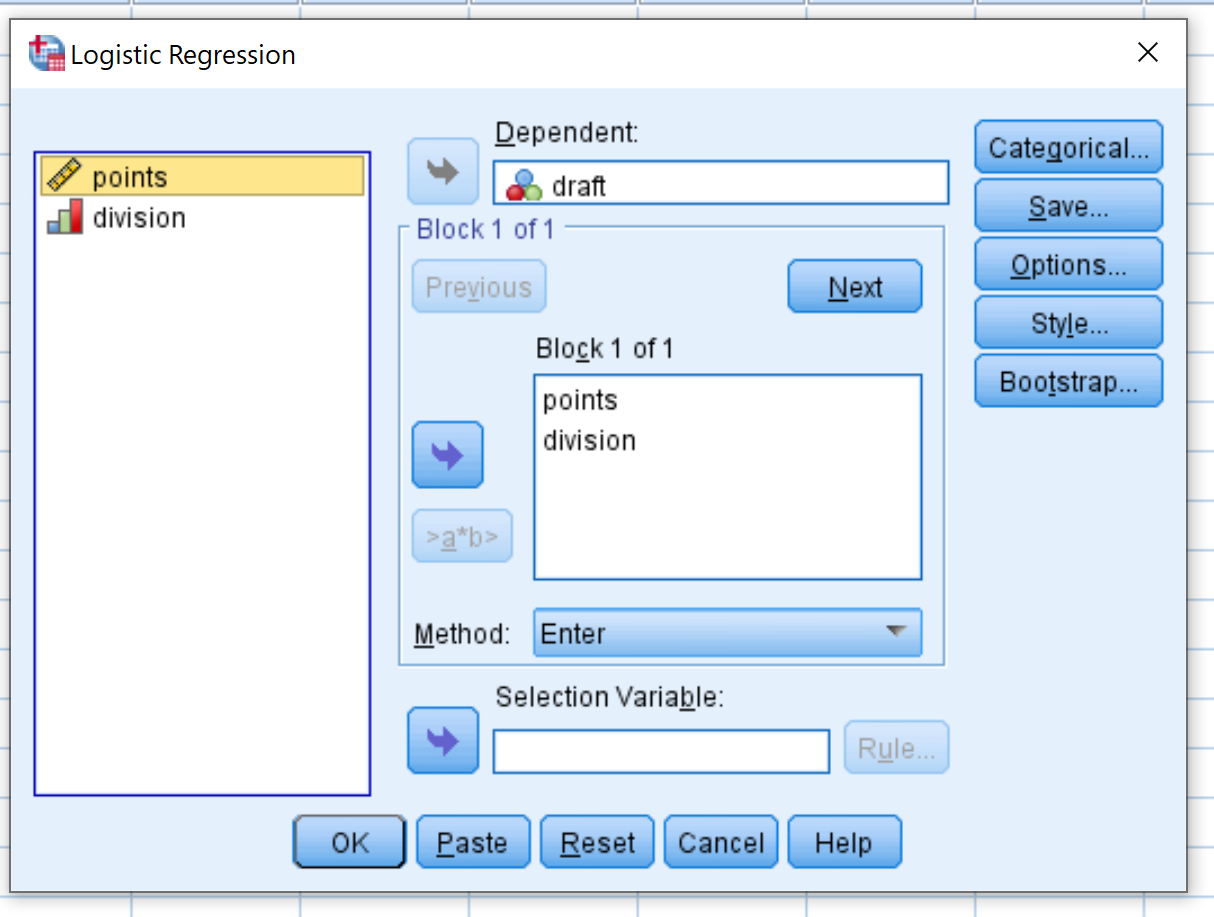
Krok 3. Zinterpretuj wynik.

Po kliknięciu OK pojawi się wynik regresji logistycznej:

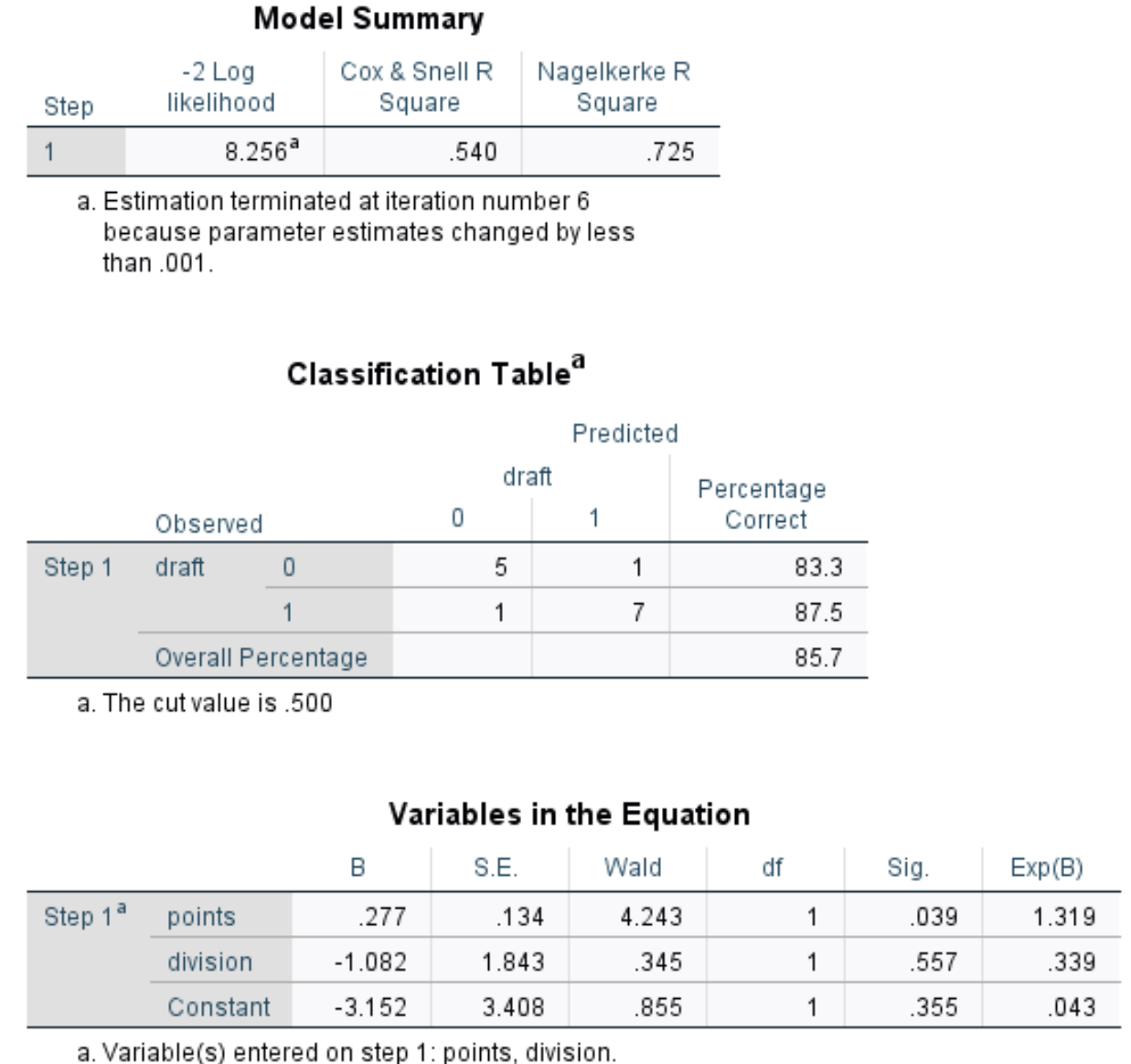
Oto jak zinterpretować wynik:

Podsumowanie modelu: Najbardziej użyteczną metryką w tej tabeli jest kwadrat Nagelkerkego R, który mówi nam, jaki procent zmienności zmiennej odpowiedzi można wyjaśnić za pomocą zmiennych predykcyjnych. W tym przypadku punkty i podział mogą wyjaśnić 72,5% zmienności zanurzenia.

Tabela klasyfikacji: Najbardziej użyteczną metryką w tej tabeli jest całkowity procent, który informuje nas o odsetku obserwacji, które model był w stanie poprawnie sklasyfikować. W tym przypadku model regresji logistycznej był w stanie poprawnie przewidzieć wynik draftu dla 85,7% graczy.

Zmienne w równaniu: Ta ostatnia tabela dostarcza nam kilku przydatnych pomiarów, w tym:

• Wald: Statystyka testu Walda dla każdej zmiennej predykcyjnej, która służy do określenia, czy każda zmienna predykcyjna jest istotna statystycznie, czy nie.
• Sig: wartość p odpowiadająca statystyce testu Walda dla każdej zmiennej predykcyjnej. Widzimy, że wartość p dla punktów wynosi 0,039, a wartość p dla dzielenia wynosi 0,557.
• Exp(B): iloraz szans dla każdej zmiennej predykcyjnej. To mówi nam, że zmiana szans gracza, który zostanie wybrany w drafcie, jest powiązana ze wzrostem o jedną jednostkę danej zmiennej prognostycznej. Na przykład szansa, że gracz Dywizji 2 zostanie wybrany w drafcie, wynosi tylko 0,339 szansy, że gracz Dywizji 1 zostanie wybrany w drafcie. Podobnie każdy dodatkowy wzrost liczby punktów na mecz wiąże się ze wzrostem szans na powołanie gracza o 1319 punktów.

Możemy wówczas wykorzystać współczynniki (wartości w kolumnie B) do przewidzenia prawdopodobieństwa powołania danego zawodnika, korzystając ze wzoru:

Prawdopodobieństwo = e ^{-3,152 + 0,277 (punkty) – 1,082 (podział)} / (1+e ^{-3,152 + 0,277 (punkty) – 1,082 (podział)} )

Na przykład prawdopodobieństwo, że zawodnik, który zdobywa średnio 20 punktów na mecz i gra w 1. lidze, zostanie wybrany do draftu, można obliczyć w następujący sposób:

Prawdopodobieństwo = e ^{-3,152 + 0,277(20) – 1,082(1)} / (1+e ^{-3,152 + 0,277(20) – 1,082(1)} ) = 0,787 .

Ponieważ prawdopodobieństwo to jest większe niż 0,5, przewidywalibyśmy, że ten gracz zostanie wybrany.

Krok 4. Ogłoś wyniki.

Na koniec chcielibyśmy przedstawić wyniki naszej regresji logistycznej. Oto przykład, jak to zrobić:

Przeprowadzono regresję logistyczną, aby określić, w jaki sposób punkty na mecz i poziom ligi wpływają na prawdopodobieństwo powołania koszykarza do draftu. W analizie wzięło udział łącznie 14 graczy.

Model wyjaśnił 72,5% zmienności wyników projektu i poprawnie sklasyfikował 85,7% przypadków.

Szansa na to, że gracz Dywizji 2 zostanie wybrany w drafcie, stanowiła zaledwie 0,339 szansy na powołanie gracza z Dywizji 1.

Każdy dodatkowy wzrost liczby punktów na mecz wiązał się ze wzrostem szans na powołanie gracza o 1319.