Jak używać invnorm na kalkulatorze ti-84 (z przykładami)

Możesz użyć funkcji invNorm() w kalkulatorze TI-84, aby znaleźć wartości krytyczne Z powiązane z rozkładem normalnym .

Ta funkcja wykorzystuje następującą składnię:

invNorm(prawdopodobieństwo, μ, σ)

Złoto:

• prawdopodobieństwo: poziom istotności
• μ: średnia populacji
• σ: odchylenie standardowe populacji

Dostęp do tej funkcji można uzyskać w kalkulatorze TI-84, naciskając przycisk 2, a następnie naciskając VARS . Spowoduje to przejście do ekranu DISTR , na którym możesz użyć invNorm() :

Poniższe przykłady pokazują, jak w praktyce wykorzystać tę funkcję.

Przykład 1: Krytyczna wartość Z dla testów jednostronnych

Załóżmy, że badacz przeprowadza test hipotezy leworęcznej, stosując α = 0,05. Jaka jest wartość krytyczna Z odpowiadająca temu poziomowi alfa?

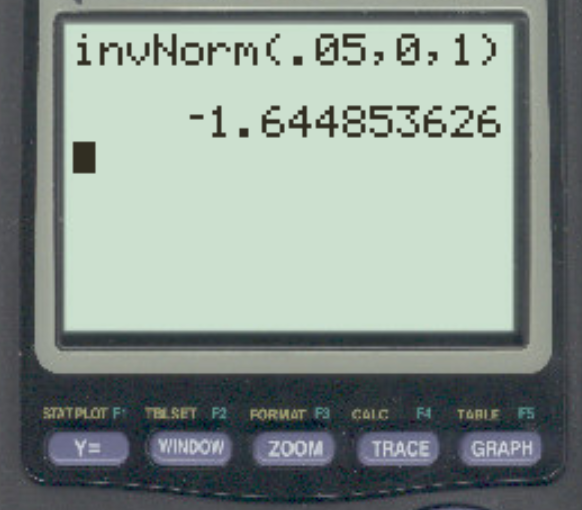
Odpowiedź brzmi z = -1,64485 .

Załóżmy, że badacz przeprowadza test hipotezy prostej, stosując α = 0,05. Jaka jest wartość krytyczna Z odpowiadająca temu poziomowi alfa?

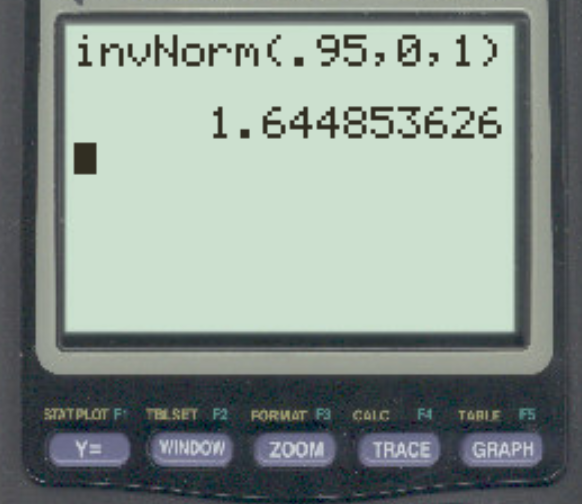
Odpowiedź brzmi z = 1,64485 .

Przykład 2: Krytyczna wartość Z dla testów dwustronnych

Załóżmy, że badacz przeprowadza dwustronny test hipotezy, stosując α = 0,05. Jaka jest wartość krytyczna Z odpowiadająca temu poziomowi alfa?

Aby znaleźć tę wartość krytyczną, możemy skorzystać ze wzoru 1 – α/2. W tym przypadku jako prawdopodobieństwo przyjmiemy 1 – 0,05/2 = 0,975:

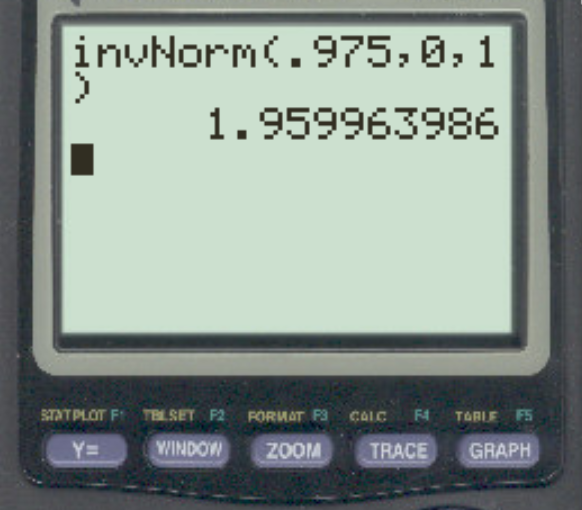
Odpowiedź brzmi z = 1,96 .

Przykład 3: Krytyczna wartość Z dla wyników odcięcia

Załóżmy, że wyniki konkretnego egzaminu mają rozkład normalny ze średnią 70 i odchyleniem standardowym 8. Jaki wynik oddziela najlepsze 10% od reszty?

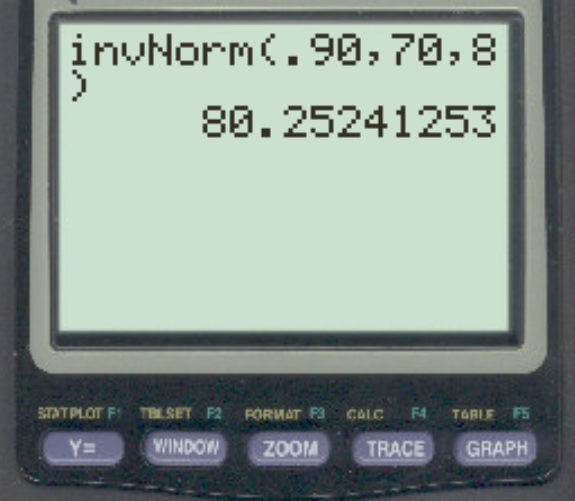
Odpowiedź to 80,25 .

Załóżmy, że wzrost mężczyzn w danym mieście ma rozkład normalny ze średnią 68 cali i odchyleniem standardowym wynoszącym 4 cale. Jak wysoko oddziela dolne 25% od reszty?

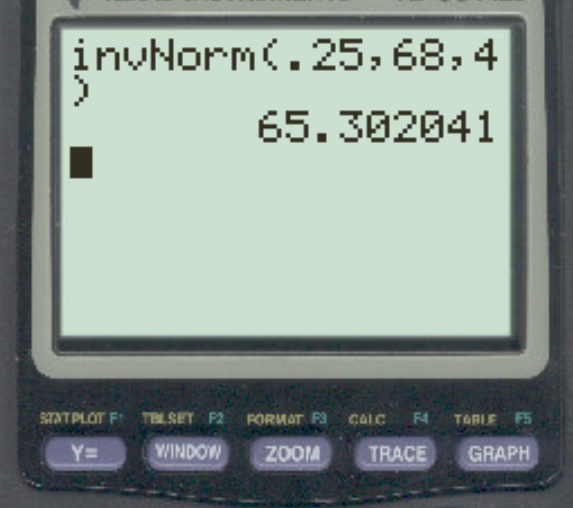
Odpowiedź brzmi: 65,3 cala.

Dodatkowe zasoby

Jak obliczyć prawdopodobieństwa dwumianowe na kalkulatorze TI-84
Jak obliczyć prawdopodobieństwa Poissona na kalkulatorze TI-84
Jak obliczyć prawdopodobieństwa geometryczne na kalkulatorze TI-84