Jak korzystać z tabeli z (z przykładami)

Tabela A z to tabela, która informuje, jaki procent wartości spada poniżej określonego wyniku Z w standardowym rozkładzie normalnym.

Wynik z pokazuje po prostu, o ile odchyleń standardowych poszczególne wartości danych spadają od średniej. Oblicza się go w następujący sposób:

wynik z = (x – μ) / σ

Złoto:

• x: indywidualna wartość danych
• μ: średnia populacji
• σ: odchylenie standardowe populacji

W tym samouczku przedstawiono kilka przykładów użycia tabeli z.

Przykład 1

Wyniki niektórych egzaminów wstępnych na studia mają rozkład normalny ze średnią μ = 82 i odchyleniem standardowym σ = 8. Jaki procent uczniów w przybliżeniu uzyskał na egzaminie wynik poniżej 84?

Krok 1: Znajdź wynik Z.

Najpierw znajdziemy wynik Z powiązany z wynikiem egzaminu wynoszącym 84:

wynik z = (x – μ) / σ = (84 – 82) / 8 = 2/8 = 0,25

Krok 2: Użyj wykresu z, aby znaleźć procent odpowiadający wynikowi z.

Następnie będziemy szukać wartości 0,25 w tabeli z:

Około 59,87% uczniów osiąga na tym egzaminie wynik poniżej 84.

Przykład 2

Wysokość roślin w pewnym ogrodzie ma rozkład normalny ze średnią μ = 26,5 cala i odchyleniem standardowym σ = 2,5 cala. Jaki procent roślin ma w przybliżeniu wysokość powyżej 26 cali?

Krok 1: Znajdź wynik Z.

Najpierw znajdziemy wskaźnik Z powiązany ze wzrostem 26 cali.

wynik z = (x – μ) / σ = (26 – 26,5) / 2,5 = -0,5 / 2,5 = -0,2

Krok 2: Użyj wykresu z, aby znaleźć procent odpowiadający wynikowi z.

Następnie będziemy szukać wartości -0,2   w tabeli z:

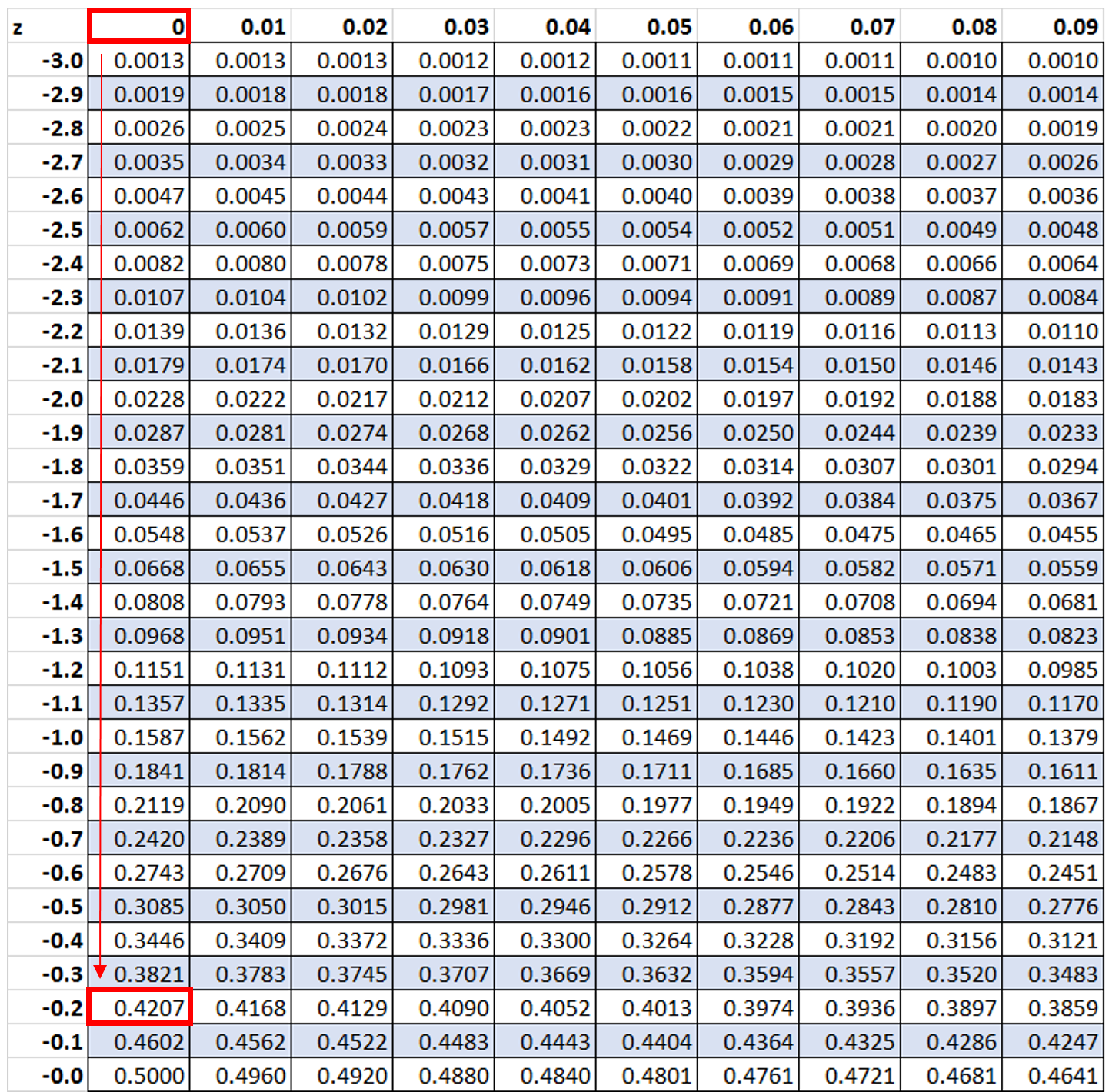
Widzimy, że 42,07% wartości jest poniżej wyniku z wynoszącego -0,2. Jednak w tym przykładzie chcemy wiedzieć, jaki procent wartości jest większy od -0,2, co możemy znaleźć korzystając ze wzoru 100% – 42,07% = 57,93%.

Zatem około 59,87% roślin w tym ogrodzie ma ponad 26 cali wysokości.

Przykład 3

Masa określonego gatunku delfinów ma rozkład normalny ze średnią μ = 400 funtów i odchyleniem standardowym σ = 25 funtów. Jaki procent delfinów waży w przybliżeniu od 410 do 425 funtów?

Krok 1: Znajdź wyniki Z.

Najpierw znajdziemy wartości Z powiązane z 410 książkami i 425 książkami

wynik z wynoszący 410 = (x – μ) / σ = (410 – 400) / 25 = 10/25 = 0,4

z wynik 425 = (x – μ) / σ = (425 – 400) / 25 = 25 / 25 = 1

Krok 2: Użyj wykresu z, aby znaleźć wartości procentowe odpowiadające każdemu wynikowi z.

Najpierw będziemy szukać wartości 0,4   w tabeli z:

Następnie będziemy szukać wartości 1   w tabeli z:

Na koniec odejmiemy najmniejszą wartość od największej: 0,8413 – 0,6554 = 0,1859 .

Tak więc około 18,59% delfinów waży od 410 do 425 funtów.

Dodatkowe zasoby

Wprowadzenie do rozkładu normalnego
Kalkulator obszaru rozkładu normalnego
Kalkulator wyniku Z