Test dopasowania chi-kwadrat na kalkulatorze ti-84

Test dobroci dopasowania chi-kwadrat służy do określenia, czy zmienna kategoryczna ma rozkład hipotetyczny.

W tym samouczku wyjaśniono, jak przeprowadzić test dopasowania chi-kwadrat na kalkulatorze TI-84.

Przykład: Test dopasowania chi-kwadrat na kalkulatorze TI-84

Właściciel sklepu twierdzi, że w każdym dniu tygodnia do jego sklepu przychodzi taka sama liczba klientów. Aby przetestować tę hipotezę, niezależny badacz rejestruje liczbę klientów, którzy przychodzą do sklepu w danym tygodniu i stwierdza, co następuje:

• Poniedziałek: 50 klientów
• Wtorek: 60 klientów
• Środa: 40 klientów
• Czwartek: 47 klientów
• Piątek: 53 klientów

Wykonamy poniższe kroki, aby przeprowadzić test dobroci dopasowania chi-kwadrat w celu ustalenia, czy dane są zgodne z twierdzeniem właściciela sklepu.

Krok 1: Wprowadź dane.

Najpierw wprowadzimy wartości danych dla oczekiwanej liczby klientów każdego dnia i obserwowanej liczby klientów każdego dnia. Naciśnij Stat , następnie naciśnij EDYTUJ . Wpisz następujące wartości dla obserwowanej liczby klientów w kolumnie L1 oraz wartości dla oczekiwanej liczby klientów w kolumnie L2:

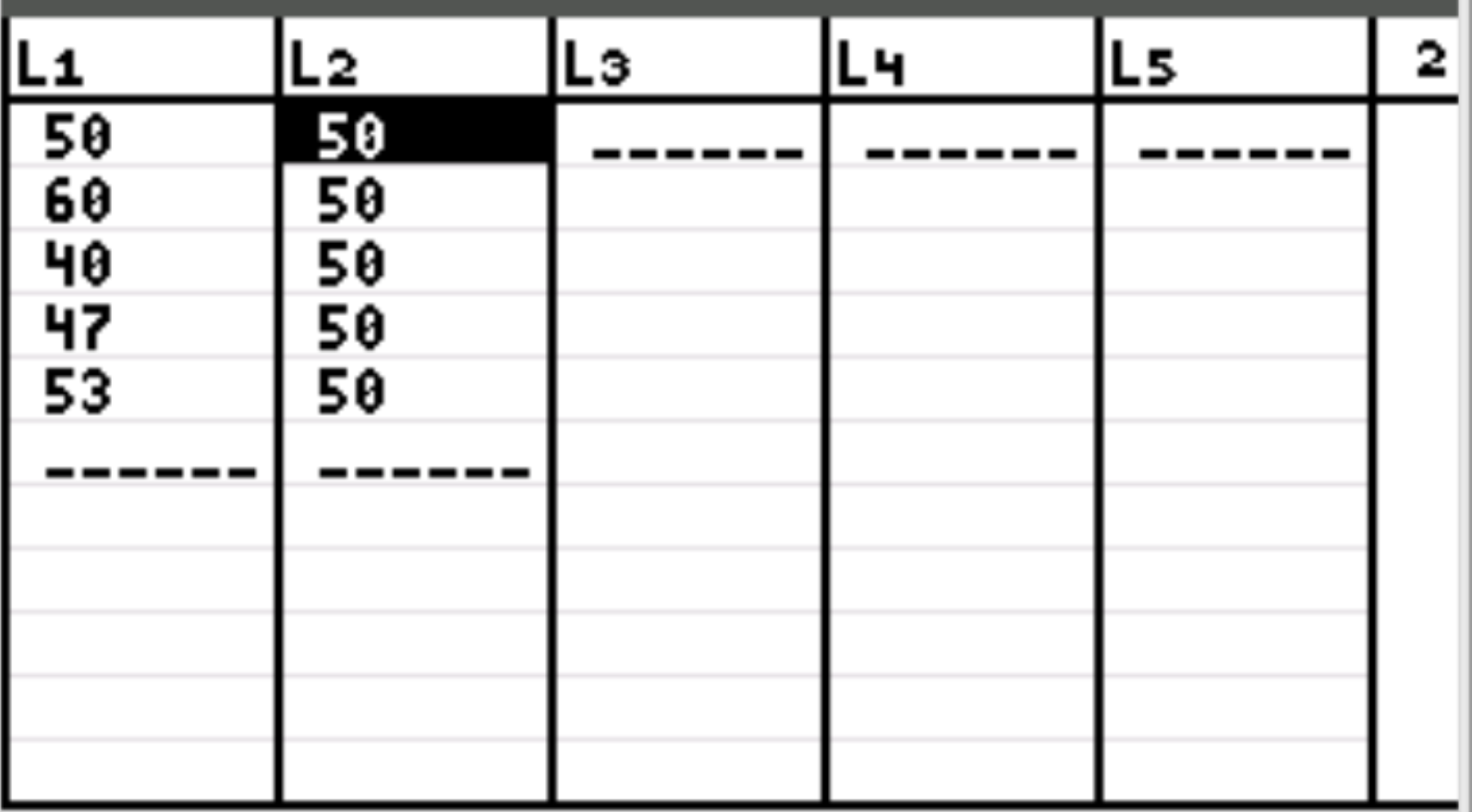
Uwaga: łącznie było 250 klientów. Jeśli więc właściciel sklepu spodziewa się, że każdego dnia do sklepu wejdzie taka sama liczba klientów, będzie to 50 klientów dziennie.

Krok 2: Wykonaj test dobroci dopasowania chi-kwadrat.

Następnie przeprowadzimy test dobroci dopasowania chi-kwadrat. Naciśnij Stat i przewiń do TESTY . Następnie przewiń w dół do X ² GOF-Test i naciśnij Enter .

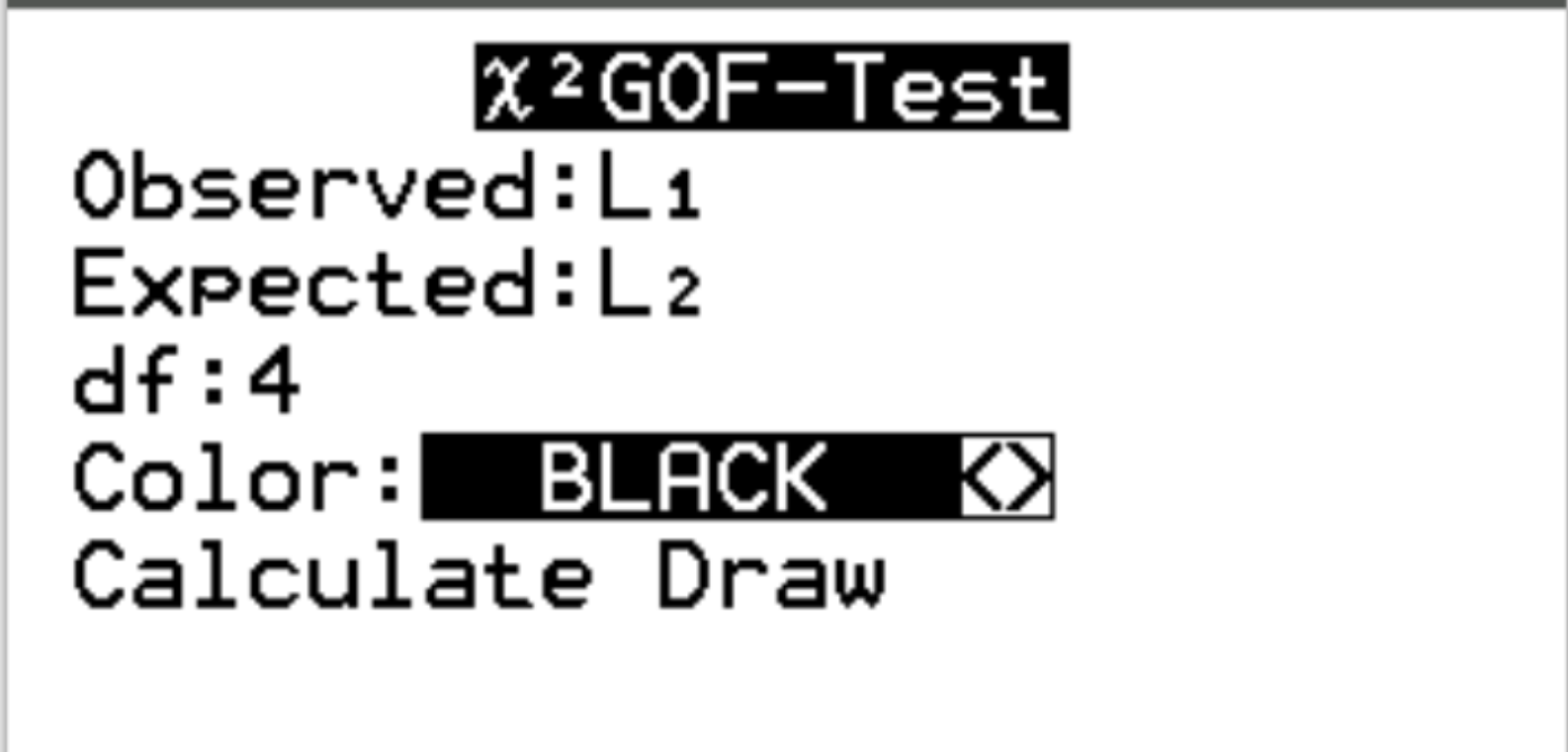
W polu Obserwowane wybierz listę L1. W polu Oczekiwane wybierz listę L2. Dla df (stopnie swobody) wpisz #kategorie – 1. W naszym przypadku mamy 5-1 = 4. Następnie zaznacz Oblicz i naciśnij Enter .

Następujące dane wyjściowe pojawią się automatycznie:

Krok 3: Interpretacja wyników.

Statystyka testu ^X2 dla testu wynosi 4,36 , a odpowiadająca jej wartość p wynosi 0,3595 . Ponieważ ta wartość p jest nie mniejsza niż 0,05, nie możemy odrzucić hipotezy zerowej. Oznacza to, że nie mamy wystarczających dowodów, aby stwierdzić, że prawdziwy rozkład klientów różni się od tego podawanego przez właściciela sklepu.