Jak wykonać regresję kwadratową na kalkulatorze ti-84

Kiedy dwie zmienne mają związek liniowy, często możemy zastosować prostą regresję liniową , aby określić ilościowo ich związek.

Jeśli jednak dwie zmienne mają związek kwadratowy, możemy zastosować regresję kwadratową do ilościowego określenia ich związku.

W tym samouczku wyjaśniono, jak przeprowadzić regresję kwadratową na kalkulatorze TI-84.

Przykład: regresja kwadratowa na kalkulatorze TI-84

Załóżmy, że chcemy zrozumieć związek pomiędzy liczbą przepracowanych godzin a szczęściem. Mamy następujące dane dotyczące liczby godzin przepracowanych tygodniowo i zgłaszanego poziomu szczęścia (w skali od 0 do 100) dla 11 różnych osób:

Wykonaj poniższe kroki, aby wykonać regresję kwadratową na kalkulatorze TI-84.

Krok 1: Wizualizuj dane.

Zanim będziemy mogli zastosować regresję kwadratową, musimy upewnić się, że związek między zmienną objaśniającą (godziny) a zmienną odpowiedzi (szczęście) jest rzeczywiście kwadratowy.

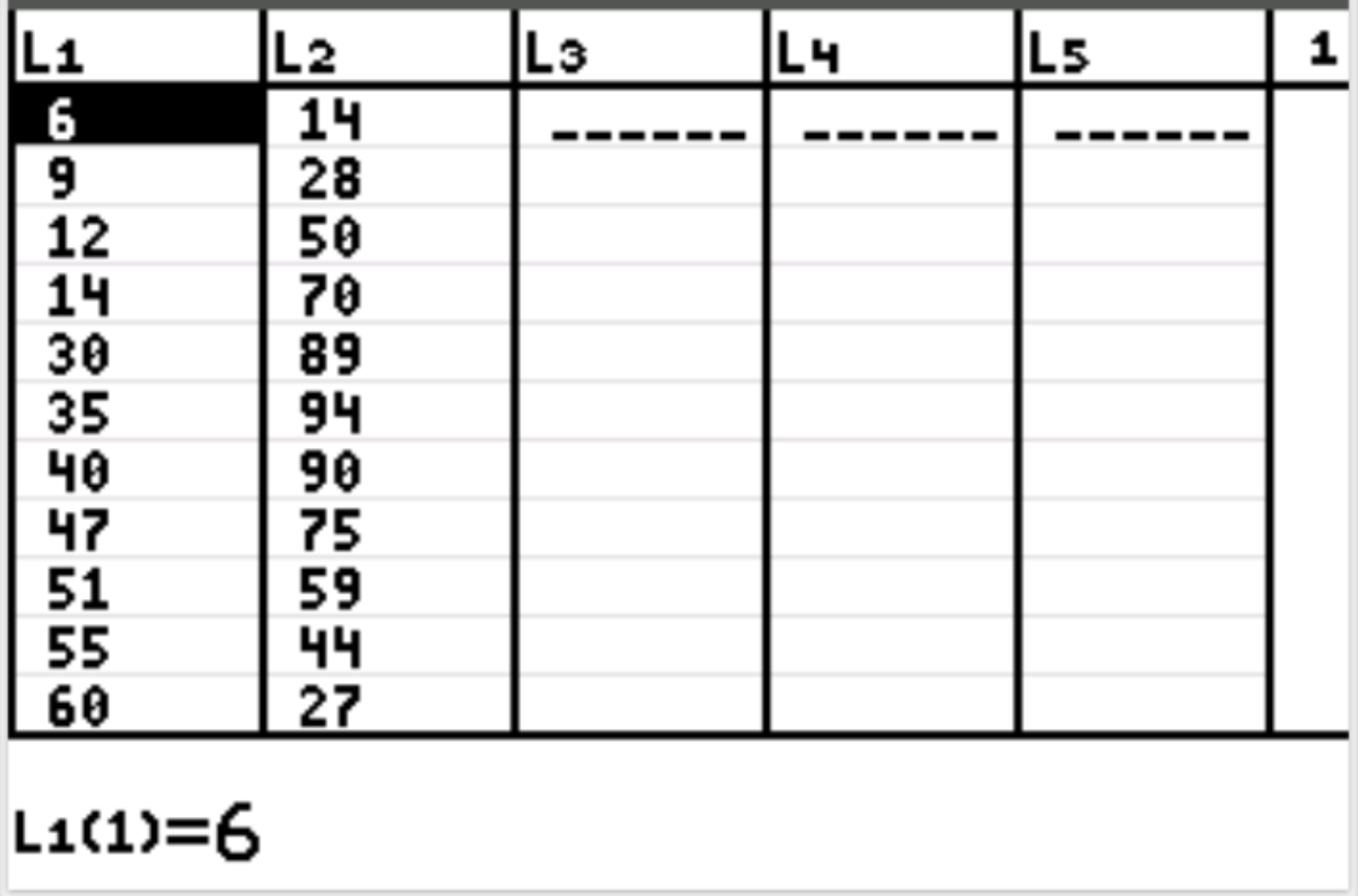
Najpierw wprowadzimy wartości danych dla zmiennej objaśniającej i zmiennej odpowiedzi. Naciśnij Stat , następnie naciśnij EDYTUJ . Wprowadź następujące wartości zmiennej objaśniającej (przepracowane godziny) w kolumnie L1 i wartości zmiennej odpowiedzi (szczęście) w kolumnie L2:

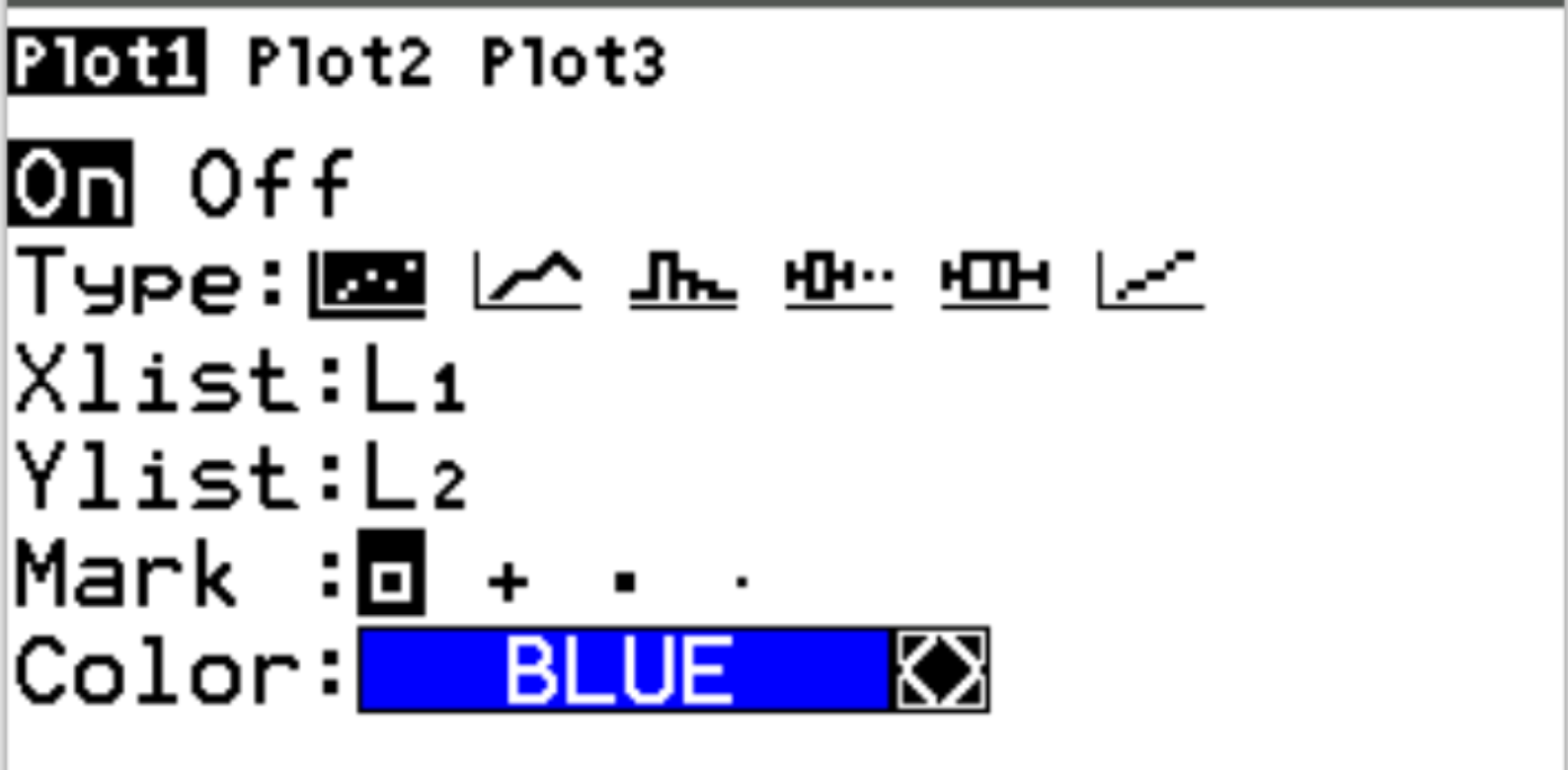
Następnie naciśnij 2nd, a następnie naciśnij y= , aby uzyskać dostęp do menu wykresu statystycznego . Podświetl Wykres1 i naciśnij Enter . Upewnij się, że kreślenie jest włączone, a L1 i L2 są wybrane odpowiednio dla Xlist i Ylist:

Następnie naciśnij Zoom , a następnie naciśnij 9:ZoomStat . Spowoduje to automatyczne utworzenie następującej chmury punktów:

Widzimy, że szczęście ma tendencję do wzrostu, gdy liczba przepracowanych godzin wzrasta od zera do pewnego punktu, ale następnie zaczyna spadać w miarę dalszego wzrostu liczby przepracowanych godzin.

Ten odwrócony kształt litery „U” na wykresie rozrzutu wskazuje, że istnieje związek kwadratowy między przepracowanymi godzinami a szczęściem, co oznacza, że do ilościowego określenia tej zależności powinniśmy użyć regresji kwadratowej.

Krok 2: Wykonaj regresję kwadratową.

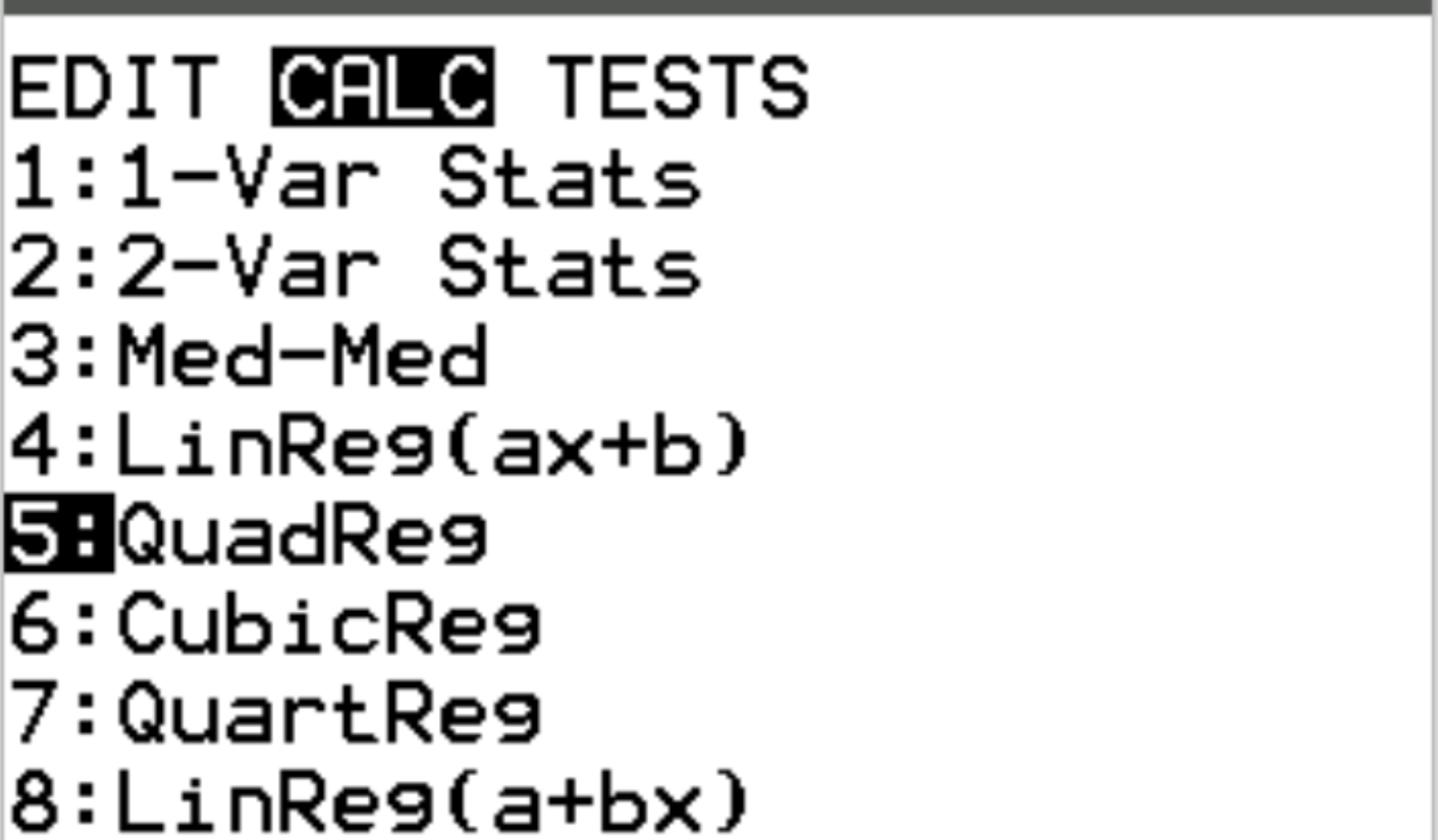
Następnie przeprowadzimy regresję kwadratową. Naciśnij Stat, a następnie przewiń do CALC . Następnie przewiń do 5:QuadReg i naciśnij Enter .

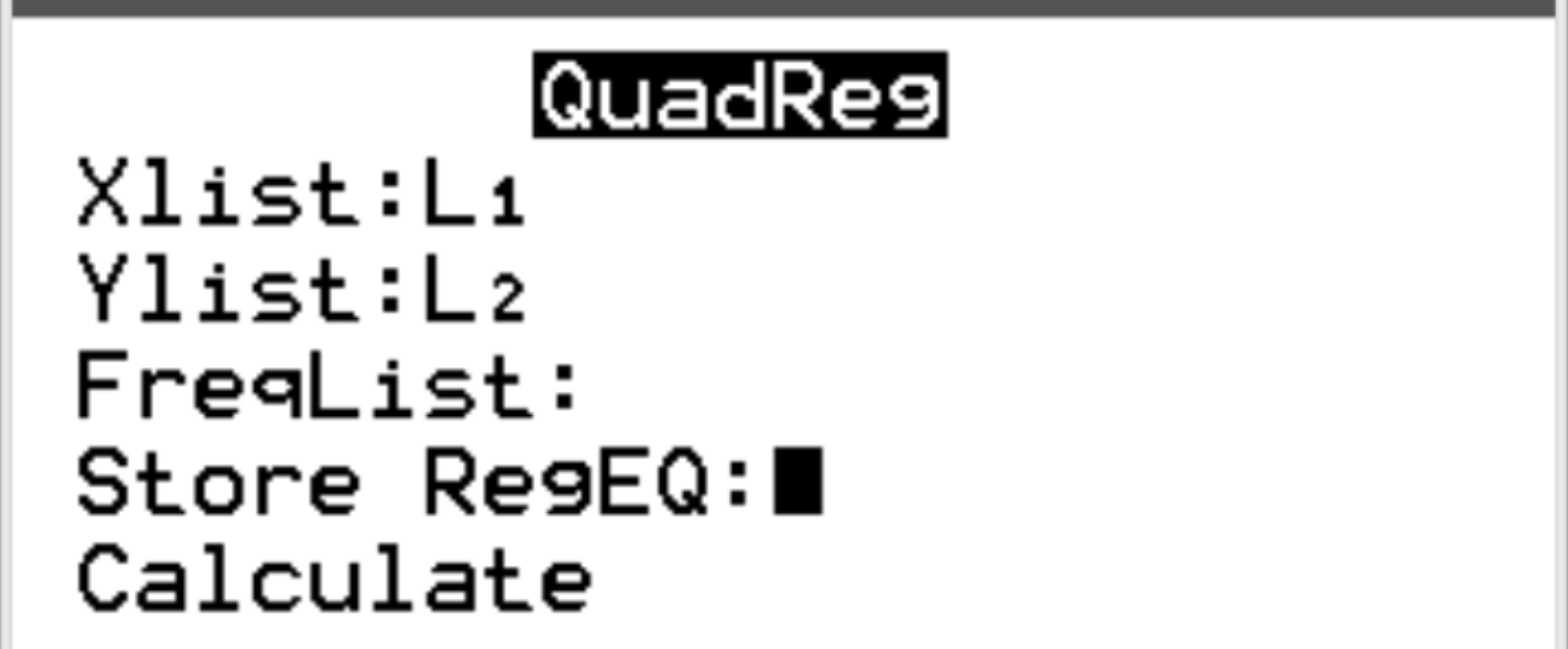
W przypadku Xlist i Ylist upewnij się, że wybrano L1 i L2, ponieważ są to kolumny, których użyliśmy do wprowadzenia naszych danych. Pozostaw listę FreqList pustą. Przewiń w dół do Oblicz i naciśnij Enter .

Następujące dane wyjściowe pojawią się automatycznie:

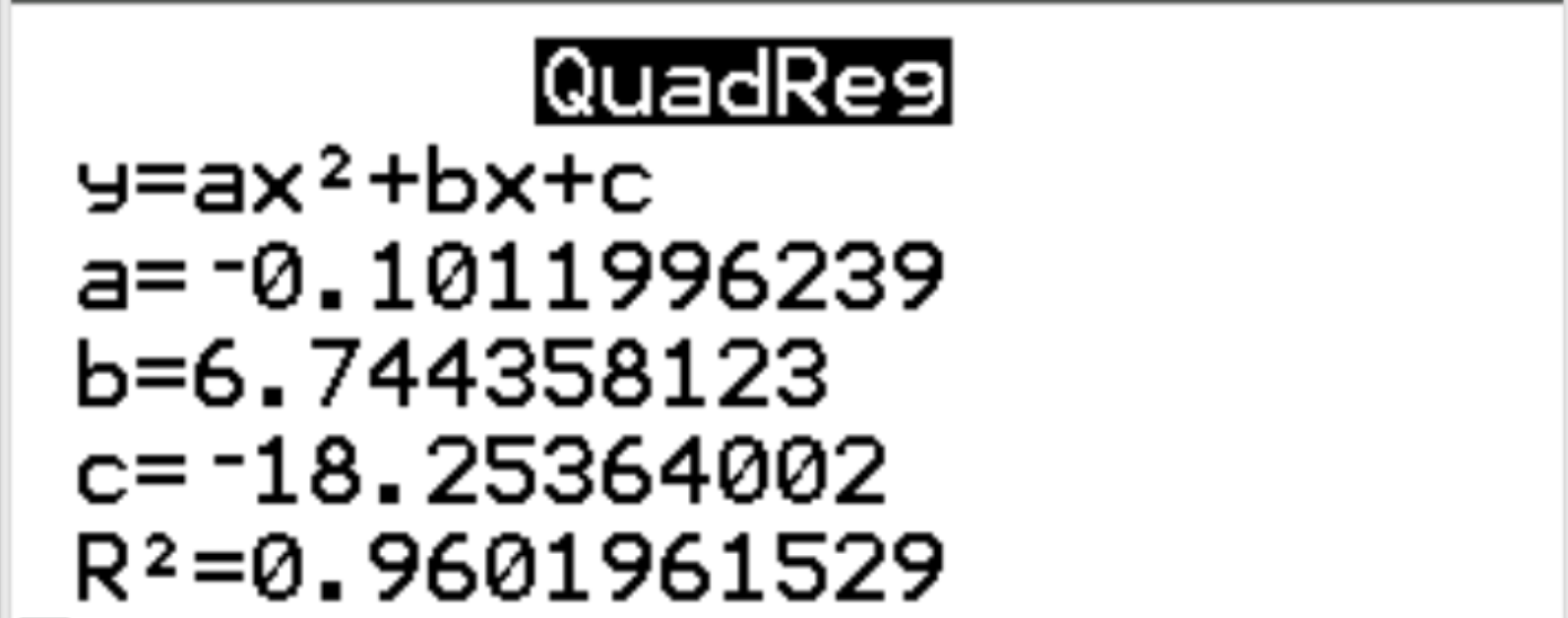
Krok 3: Zinterpretuj wynik.

Z wyników widzimy, że oszacowane równanie regresji ma postać:

szczęście = -0,1012 (godzin) ² + 6,7444 (godzin) – 18,2536

Możemy użyć tego równania, aby znaleźć przewidywane szczęście danej osoby, biorąc pod uwagę liczbę godzin przepracowanych w tygodniu.

Na przykład osoba pracująca 60 godzin tygodniowo miałaby poziom szczęścia równy 22,09 :

szczęście = -0,1012(60) ² + 6,7444(60) – 18,2536 = 22,09

I odwrotnie, osoba pracująca 30 godzin tygodniowo powinna mieć poziom szczęścia na poziomie 92,99 :

szczęście = -0,1012(30) ² + 6,7444(30) – 18,2536 = 92,99

Widzimy również, że r kwadrat dla modelu regresji wynosi r ² = 0,9602 . Jest to proporcja wariancji zmiennej odpowiedzi, którą można wyjaśnić za pomocą zmiennych objaśniających. W tym przykładzie 96,02% zróżnicowania szczęścia można wyjaśnić godzinami i godzinami ² .