Jaki jest kompromis wariancji odchylenia w uczeniu maszynowym?

Aby ocenić wydajność modelu na zbiorze danych, musimy zmierzyć, jak dobrze przewidywania modelu odpowiadają obserwowanym danym.

W przypadku modeli regresji najczęściej stosowaną metryką jest błąd średniokwadratowy (MSE), który oblicza się w następujący sposób:

MSE = (1/n)*Σ(y _i – f(x _i )) ²

Złoto:

• n: całkowita liczba obserwacji
• y _i : Wartość odpowiedzi i ^-tej obserwacji
• f(x _i ): Przewidywana wartość odpowiedzi i- ^tej obserwacji

Im bardziej prognozy modelu będą zbliżone do obserwacji, tym niższy będzie MSE.

Nas jednak interesuje tylko test MSE – MSE, gdy nasz model zostanie zastosowany do niewidocznych danych. Dzieje się tak, ponieważ interesuje nas tylko to, jak model będzie działał na nieznanych danych, a nie na istniejących danych.

Na przykład nie ma nic złego w tym, że model przewidujący ceny akcji ma niski współczynnik MSE na danych historycznych, ale naprawdę chcemy móc używać tego modelu do dokładnego przewidywania przyszłych danych.

Okazuje się, że test MSE nadal można podzielić na dwie części:

(1) Wariancja: odnosi się do wielkości, o jaką zmieniłaby się nasza funkcja f , gdybyśmy oszacowali ją przy użyciu innego zbioru uczącego.

(2) Błąd: odnosi się do błędu spowodowanego podejściem do rzeczywistego problemu, który może być niezwykle skomplikowany, za pomocą znacznie prostszego modelu.

Zapisane w kategoriach matematycznych:

Test MSE = Var( f̂( x ₀ )) + [Odchylenie ( f̂( x ₀ ))] ² + Var(ε)

Test MSE = wariancja + błąd ² + błąd nieredukowalny

Trzeci składnik, błąd nieredukowalny, to błąd, którego nie można zredukować za pomocą żadnego modelu po prostu dlatego, że w relacji między zbiorem zmiennych objaśniających a zmienną odpowiedzi zawsze występuje szum .

Modele o dużym obciążeniu mają zwykle niską wariancję . Na przykład modele regresji liniowej mają zwykle duże obciążenie (zakładając prostą liniową zależność między zmiennymi objaśniającymi a zmienną odpowiedzi) i niską wariancję (oszacowania modelu nie będą się zbytnio zmieniać w zależności od próbki). inny).

Jednak modele o niskim obciążeniu mają zwykle dużą wariancję . Na przykład złożone modele nieliniowe mają zwykle niskie obciążenie (nie zakłada się określonego związku między zmiennymi objaśniającymi a zmienną odpowiedzi) i dużą wariancję (oszacowania modelu mogą znacznie zmieniać się w zależności od próbki uczenia się).

Kompromis odchylenia i wariancji

Kompromis odchylenie-wariancja odnosi się do kompromisu, który ma miejsce, gdy zdecydujemy się zmniejszyć odchylenie, co ogólnie zwiększa wariancję, lub zmniejszyć wariancję, co ogólnie zwiększa odchylenie.

Poniższy wykres pozwala zwizualizować ten kompromis:

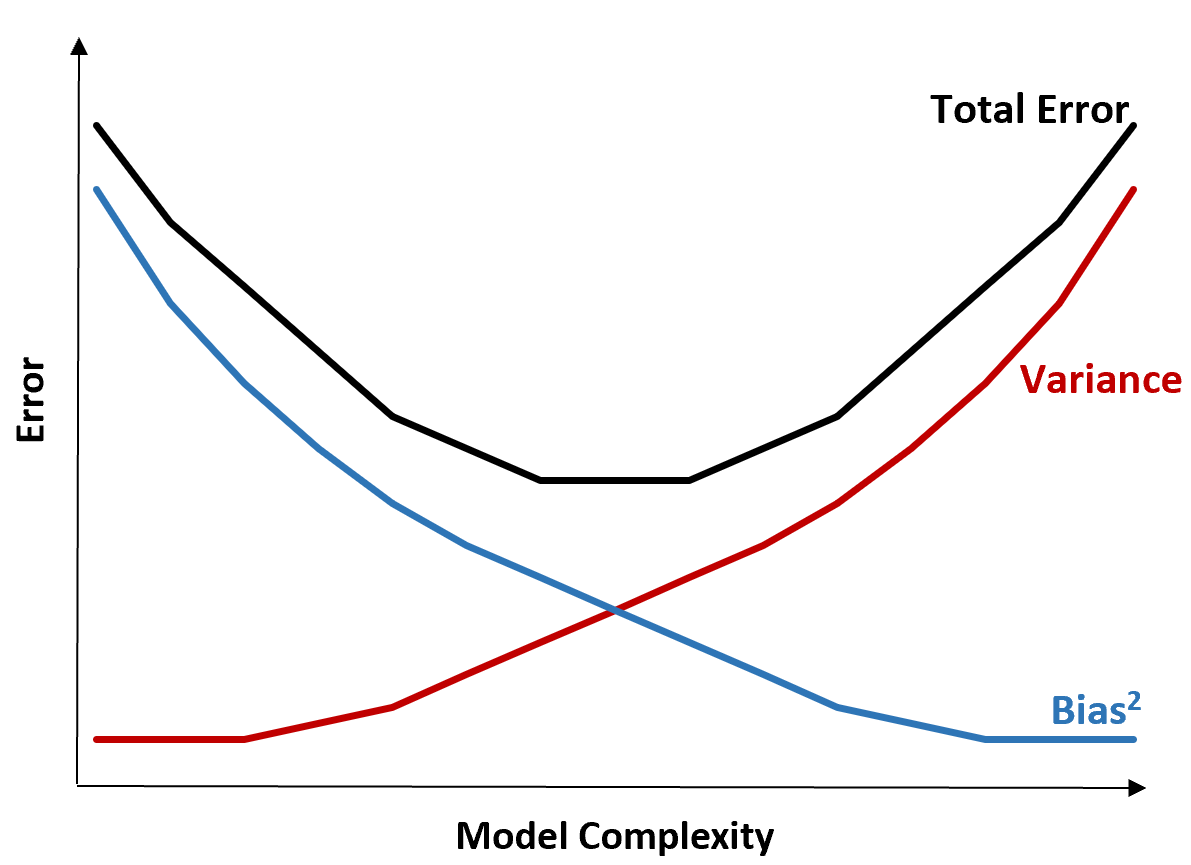
Błąd całkowity maleje wraz ze wzrostem złożoności modelu, ale tylko do pewnego punktu. Po przekroczeniu pewnego punktu wariancja zaczyna rosnąć, a błąd całkowity również zaczyna rosnąć.

W praktyce zależy nam jedynie na minimalizacji całkowitego błędu modelu, niekoniecznie minimalizacji wariancji czy błędu systematycznego. Okazuje się, że sposobem na zminimalizowanie błędu całkowitego jest znalezienie właściwej równowagi między wariancją a obciążeniem.

Innymi słowy, chcemy modelu wystarczająco złożonego, aby uchwycić prawdziwy związek między zmiennymi objaśniającymi a zmienną odpowiedzi, ale niezbyt skomplikowanego, aby wykryć wzorce, które w rzeczywistości nie istnieją.

Kiedy model jest zbyt złożony, powoduje nadmierne dopasowanie do danych. Dzieje się tak, ponieważ zbyt trudno jest znaleźć wzorce w danych uczących, które są po prostu spowodowane przypadkiem. Ten typ modelu prawdopodobnie będzie słabo działał na niewidocznych danych.

Kiedy jednak model jest zbyt prosty, powoduje to niedoszacowanie danych. Dzieje się tak, ponieważ zakłada się, że prawdziwa zależność pomiędzy zmiennymi objaśniającymi a zmienną odpowiedzią jest prostsza niż jest w rzeczywistości.

Sposobem wyboru optymalnych modeli w uczeniu maszynowym jest znalezienie równowagi między obciążeniem a wariancją, aby zminimalizować błąd testowania modelu na przyszłych, niewidocznych danych.

W praktyce najczęstszym sposobem minimalizacji MSE testów jest zastosowanie walidacji krzyżowej .