Dopasowanie krzywej w r (z przykładami)

Często możesz chcieć znaleźć równanie, które najlepiej pasuje do krzywej R.

Poniższy przykład wyjaśnia krok po kroku, jak dopasować krzywe do danych w R za pomocą funkcji Poly() i jak określić, która krzywa najlepiej pasuje do danych.

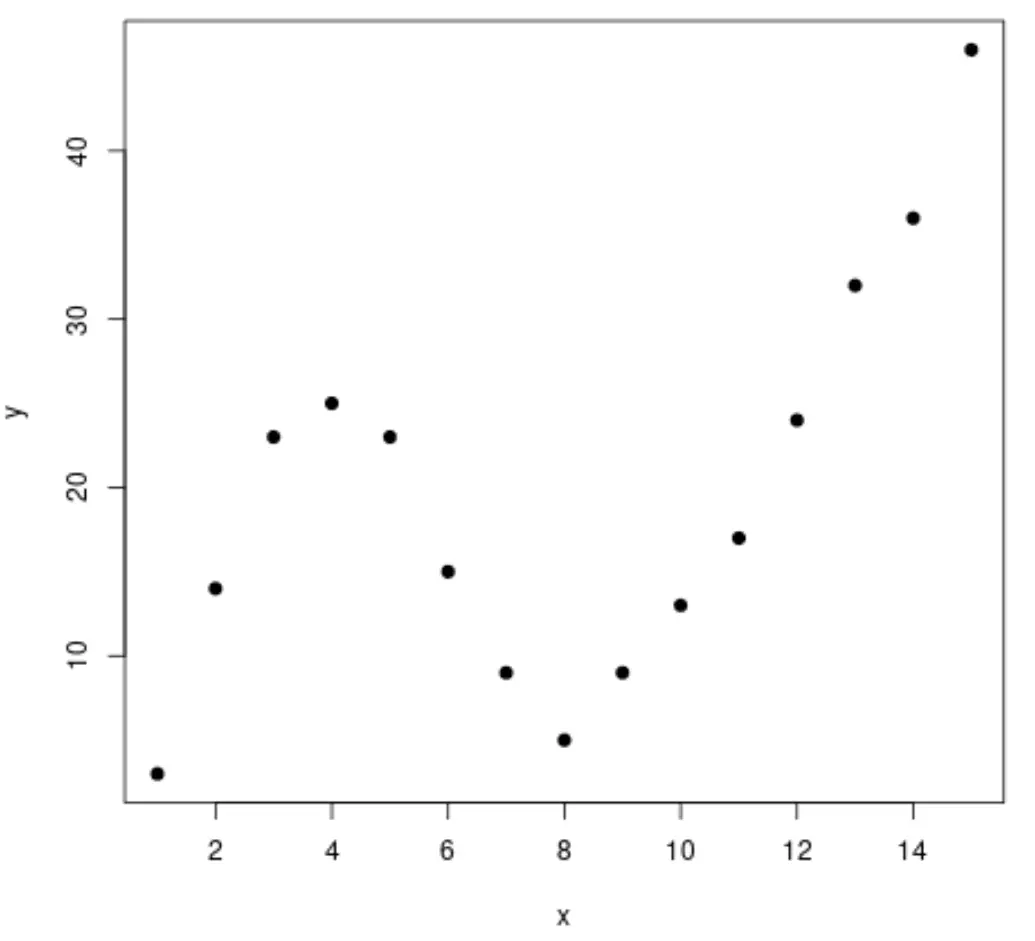
Krok 1: Utwórz i wizualizuj dane

Zacznijmy od utworzenia fałszywego zbioru danych, a następnie utwórz wykres rozrzutu w celu wizualizacji danych:

 #create data frame
df <- data. frame (x=1:15,
                 y=c(3, 14, 23, 25, 23, 15, 9, 5, 9, 13, 17, 24, 32, 36, 46))

#create a scatterplot of x vs. y
plot(df$x, df$y, pch= 19 , xlab=' x ', ylab=' y ') 

Krok 2: Dostosuj wiele krzywych

Dopasujmy następnie do danych kilka modeli regresji wielomianowej i zwizualizujmy krzywą każdego modelu na tym samym wykresie:

 #fit polynomial regression models up to degree 5
fit1 <- lm(y~x, data=df)
fit2 <- lm(y~poly(x,2,raw= TRUE ), data=df)
fit3 <- lm(y~poly(x,3,raw= TRUE ), data=df)
fit4 <- lm(y~poly(x,4,raw= TRUE ), data=df)
fit5 <- lm(y~poly(x,5,raw= TRUE ), data=df)

#create a scatterplot of x vs. y
plot(df$x, df$y, pch=19, xlab=' x ', ylab=' y ')

#define x-axis values
x_axis <- seq(1, 15, length= 15 )

#add curve of each model to plot
lines(x_axis, predict(fit1, data. frame (x=x_axis)), col=' green ')
lines(x_axis, predict(fit2, data. frame (x=x_axis)), col=' red ')
lines(x_axis, predict(fit3, data. frame (x=x_axis)), col=' purple ')
lines(x_axis, predict(fit4, data. frame (x=x_axis)), col=' blue ')
lines(x_axis, predict(fit5, data. frame (x=x_axis)), col=' orange ')

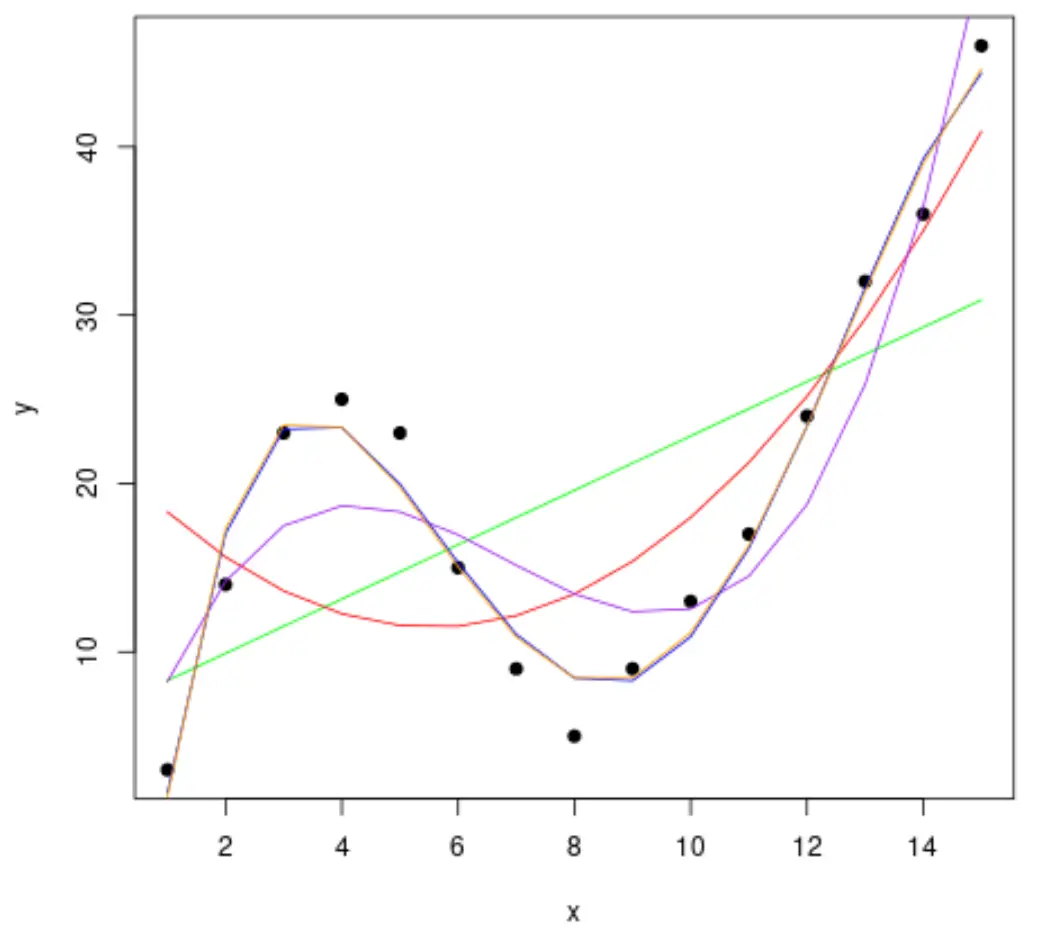
Aby określić, która krzywa najlepiej pasuje do danych, możemy spojrzeć na skorygowany kwadrat R każdego modelu.

Wartość ta mówi nam, jaki procent zmienności zmiennej odpowiedzi można wyjaśnić za pomocą zmiennych predykcyjnych w modelu, skorygowanych o liczbę zmiennych predykcyjnych.

 #calculated adjusted R-squared of each model
summary(fit1)$adj. r . squared
summary(fit2)$adj. r . squared
summary(fit3)$adj. r . squared
summary(fit4)$adj. r . squared
summary(fit5)$adj. r . squared

[1] 0.3144819
[1] 0.5186706
[1] 0.7842864
[1] 0.9590276
[1] 0.9549709

Z wyniku widać, że model z najwyższym skorygowanym współczynnikiem R-kwadrat jest wielomianem czwartego stopnia, którego skorygowany współczynnik R-kwadrat wynosi 0,959 .

Krok 3: Wizualizuj ostateczną krzywą

Na koniec możemy utworzyć wykres punktowy z krzywą modelu wielomianowego czwartego stopnia:

 #create a scatterplot of x vs. y
plot(df$x, df$y, pch=19, xlab=' x ', ylab=' y ')

#define x-axis values
x_axis <- seq(1, 15, length= 15 )

#add curve of fourth-degree polynomial model
lines(x_axis, predict(fit4, data. frame (x=x_axis)), col=' blue ')

Równanie dla tej linii możemy również uzyskać za pomocą funkcji podsumowania() :

 summary(fit4)

Call:
lm(formula = y ~ poly(x, 4, raw = TRUE), data = df)

Residuals:
    Min 1Q Median 3Q Max 
-3.4490 -1.1732 0.6023 1.4899 3.0351 

Coefficients:
                         Estimate Std. Error t value Pr(>|t|)    
(Intercept) -26.51615 4.94555 -5.362 0.000318 ***
poly(x, 4, raw = TRUE)1 35.82311 3.98204 8.996 4.15e-06 ***
poly(x, 4, raw = TRUE)2 -8.36486 0.96791 -8.642 5.95e-06 ***
poly(x, 4, raw = TRUE)3 0.70812 0.08954 7.908 1.30e-05 ***
poly(x, 4, raw = TRUE)4 -0.01924 0.00278 -6.922 4.08e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.424 on 10 degrees of freedom
Multiple R-squared: 0.9707, Adjusted R-squared: 0.959 
F-statistic: 82.92 on 4 and 10 DF, p-value: 1.257e-07

Równanie krzywej jest następujące:

y = -0,0192x ⁴ + 0,7081x ³ – 8,3649x ² + 35,823x – 26,516

Możemy użyć tego równania do przewidzenia wartościzmiennej odpowiedzi na podstawie zmiennych predykcyjnych w modelu. Na przykład, jeśli x = 4, to przewidywalibyśmy, że y = 23,34 :

y = -0,0192(4) ⁴ + 0,7081(4) ³ – 8,3649(4) ² + 35,823(4) – 26,516 = 23,34

Dodatkowe zasoby

Wprowadzenie do regresji wielomianowej
Regresja wielomianowa w R (krok po kroku)
Jak korzystać z funkcji seq w R