Jak wykonać regresję splajnu w r (z przykładem)

Regresja sklejana to rodzaj regresji stosowany w przypadku punktów lub „węzłów”, w których wzór danych zmienia się gwałtownie, a regresja liniowa i regresja wielomianowa nie są wystarczająco elastyczne, aby dopasować się do danych.

Poniższy przykład pokazuje krok po kroku, jak wykonać regresję splajnową w R.

Krok 1: Utwórz dane

Najpierw utwórzmy zbiór danych w R z dwiema zmiennymi i utwórzmy wykres rozrzutu, aby zwizualizować relację między zmiennymi:

 #create data frame
df <- data. frame (x=1:20,
                 y=c(2, 4, 7, 9, 13, 15, 19, 16, 13, 10,
                     11, 14, 15, 15, 16, 15, 17, 19, 18, 20))

#view head of data frame
head(df)

  xy
1 1 2
2 2 4
3 3 7
4 4 9
5 5 13
6 6 15

#create scatterplot
plot(df$x, df$y, cex= 1.5 , pch= 19 )

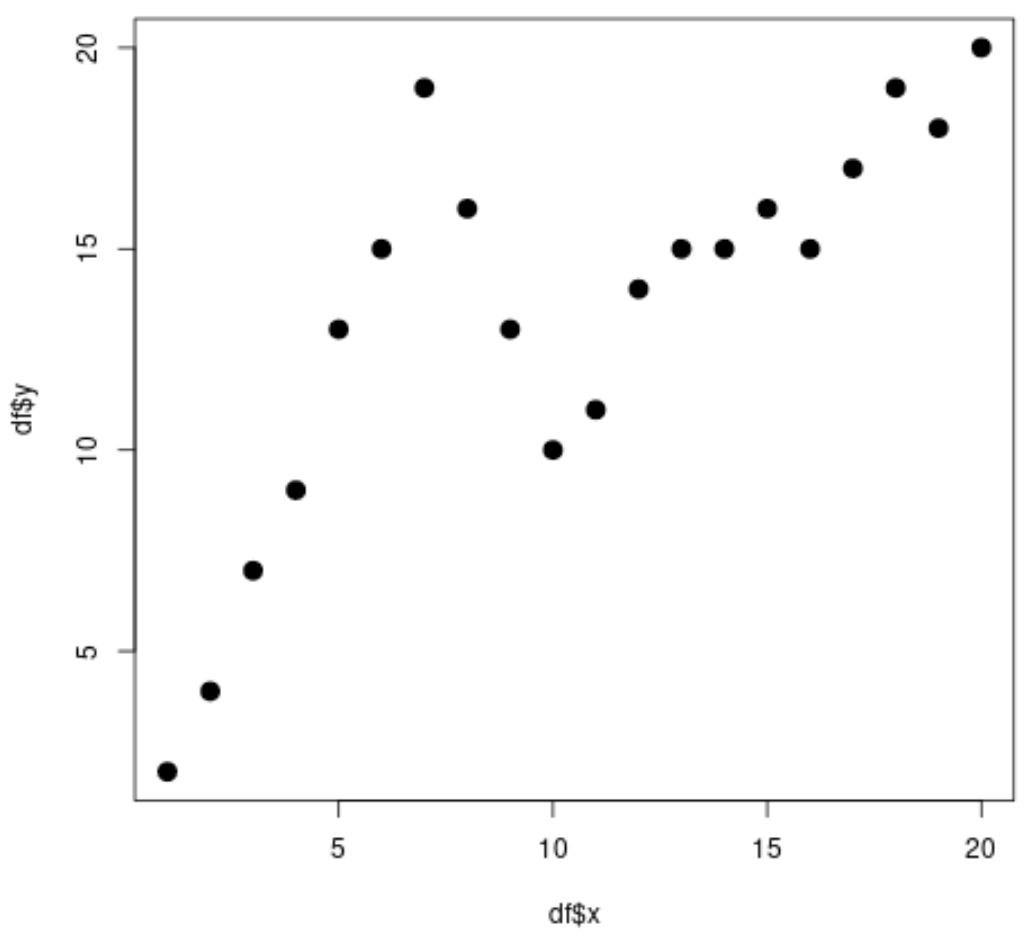
Oczywiście związek między x i y jest nieliniowy i wydaje się, że istnieją dwa punkty lub „węzły”, w których wzór danych zmienia się gwałtownie przy x=7 i x=10.

Krok 2: Dopasuj prosty model regresji liniowej

Użyjmy następnie funkcji lm(), aby dopasować prosty model regresji liniowej do tego zbioru danych i wykreślmy dopasowaną linię regresji na wykresie rozrzutu:

 #fit simple linear regression model
linear_fit <- lm(df$y ~ df$x)

#view model summary
summary(linear_fit)

Call:
lm(formula = df$y ~ df$x)

Residuals:
    Min 1Q Median 3Q Max 
-5.2143 -1.6327 -0.3534 0.6117 7.8789 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 6.5632 1.4643 4.482 0.000288 ***
df$x 0.6511 0.1222 5.327 4.6e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.152 on 18 degrees of freedom
Multiple R-squared: 0.6118, Adjusted R-squared: 0.5903 
F-statistic: 28.37 on 1 and 18 DF, p-value: 4.603e-05

#create scatterplot
plot(df$x, df$y, cex= 1.5 , pch= 19 )

#add regression line to scatterplot
abline(linear_fit) 

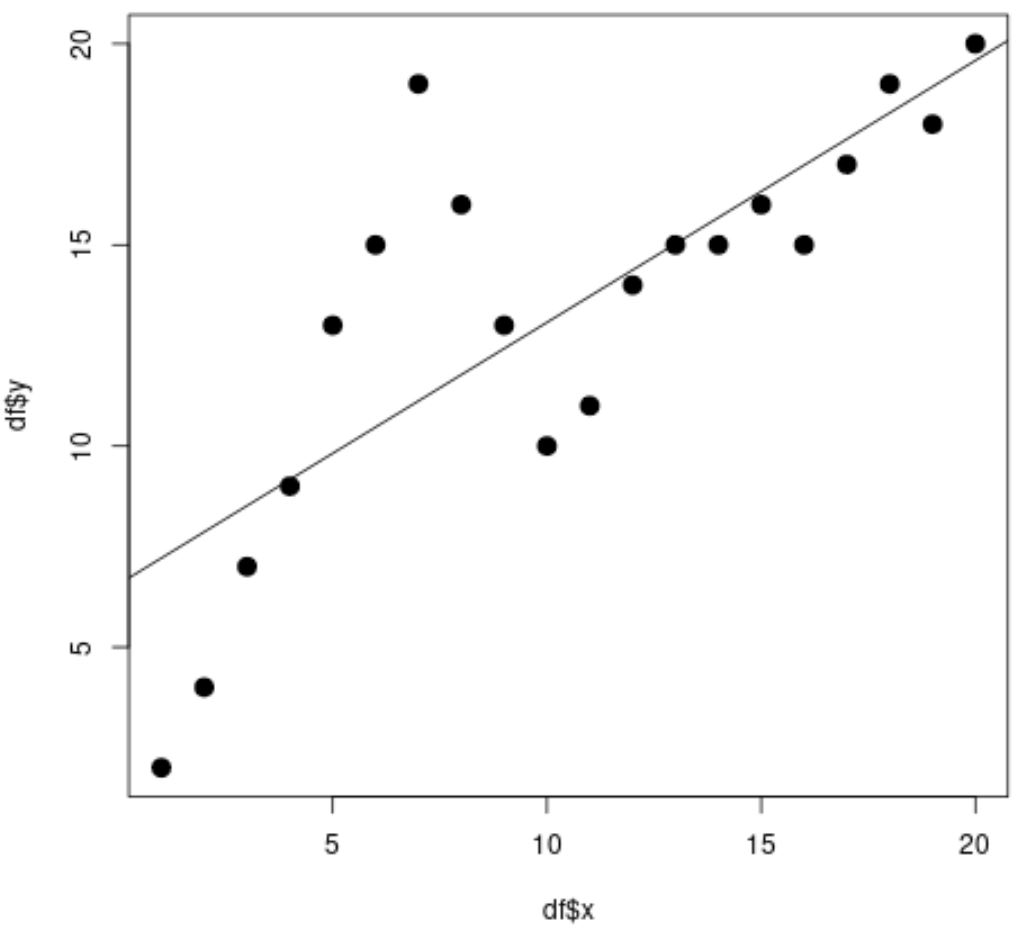
Z wykresu rozrzutu widzimy, że prosta linia regresji liniowej nie pasuje dobrze do danych.

Z wyników modelu możemy również zobaczyć, że skorygowana wartość R-kwadrat wynosi 0,5903 .

Porównamy to z skorygowaną wartością R-kwadrat modelu splajnowego.

Krok 3: Dopasuj model regresji splajnowej

Następnie użyjmy funkcji bs() z pakietu splines , aby dopasować model regresji spline z dwoma węzłami, a następnie wykreślmy dopasowany model na wykresie rozrzutu:

 library (splines)

#fit spline regression model
spline_fit <- lm(df$y ~ bs(df$x, knots=c( 7 , 10 )))

#view summary of spline regression model
summary(spline_fit)

Call:
lm(formula = df$y ~ bs(df$x, knots = c(7, 10)))

Residuals:
     Min 1Q Median 3Q Max 
-2.84883 -0.94928 0.08675 0.78069 2.61073 

Coefficients:
                            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 2.073 1.451 1.429 0.175    
bs(df$x, knots = c(7, 10))1 2.173 3.247 0.669 0.514    
bs(df$x, knots = c(7, 10))2 19.737 2.205 8.949 3.63e-07 ***
bs(df$x, knots = c(7, 10))3 3.256 2.861 1.138 0.274    
bs(df$x, knots = c(7, 10))4 19.157 2.690 7.121 5.16e-06 ***
bs(df$x, knots = c(7, 10))5 16.771 1.999 8.391 7.83e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.568 on 14 degrees of freedom
Multiple R-squared: 0.9253, Adjusted R-squared: 0.8987 
F-statistic: 34.7 on 5 and 14 DF, p-value: 2.081e-07

#calculate predictions using spline regression model
x_lim <- range(df$x)
x_grid <- seq(x_lim[ 1 ], x_lim[ 2 ])
preds <- predict(spline_fit, newdata=list(x=x_grid))

#create scatter plot with spline regression predictions
plot(df$x, df$y, cex= 1.5 , pch= 19 )
lines(x_grid, preds) 

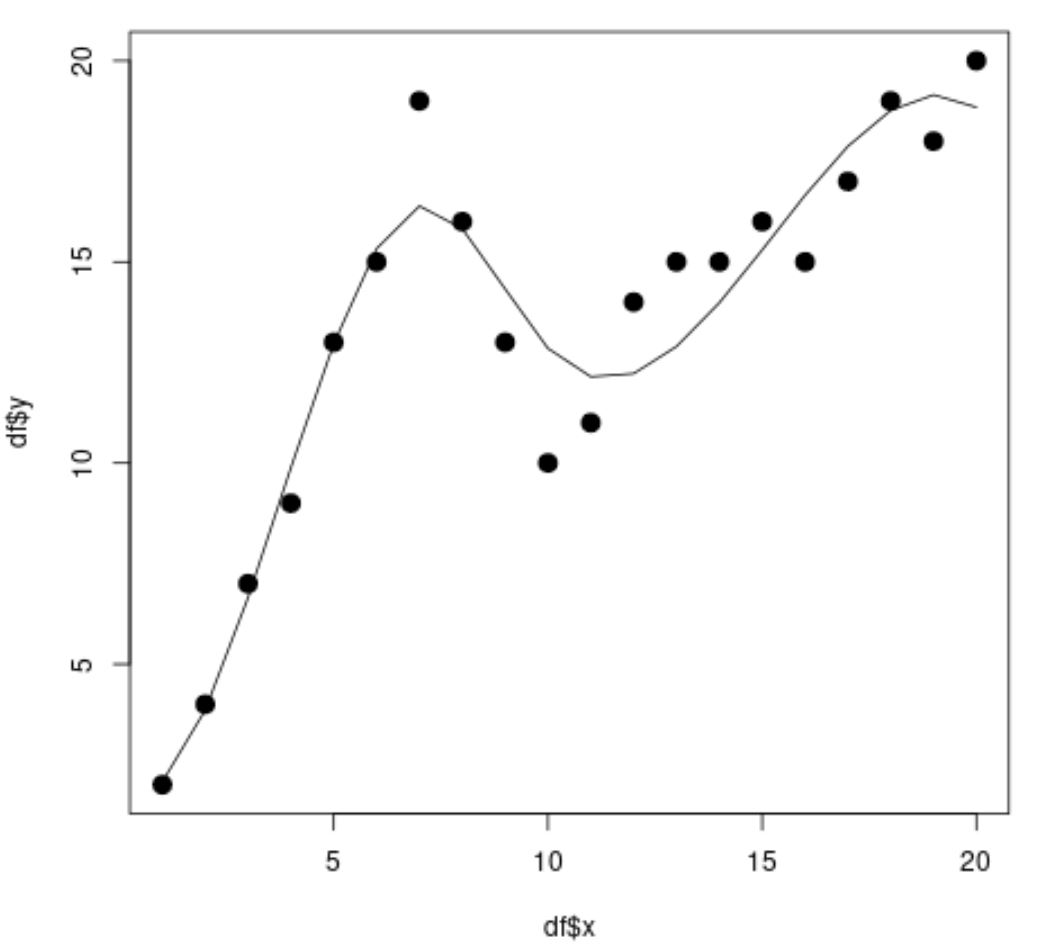
Z wykresu rozrzutu widzimy, że model regresji splajnowej jest w stanie całkiem dobrze dopasować dane.

Z wyników modelu możemy również zobaczyć, że skorygowana wartość R-kwadrat wynosi 0,8987 .

Skorygowana wartość R-kwadrat dla tego modelu jest znacznie wyższa niż w przypadku prostego modelu regresji liniowej, co mówi nam, że model regresji sklejanej jest w stanie lepiej dopasować dane.

Zauważ, że w tym przykładzie wybraliśmy, że węzły znajdują się w x=7 i x=10.

W praktyce będziesz musiał samodzielnie wybrać lokalizacje węzłów w oparciu o miejsca, w których wzorce w danych wydają się zmieniać, oraz w oparciu o wiedzę specjalistyczną w Twojej dziedzinie.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe zadania w języku R:

Jak wykonać wielokrotną regresję liniową w R
Jak przeprowadzić regresję wykładniczą w R
Jak wykonać ważoną regresję metodą najmniejszych kwadratów w R