Regresja wykładnicza w r (krok po kroku)

Regresja wykładnicza to rodzaj regresji, który można zastosować do modelowania następujących sytuacji:

1. Wzrost wykładniczy: Wzrost zaczyna się powoli, a następnie przyspiesza szybko i bez ograniczeń.

2. Zanik wykładniczy: Rozpad zaczyna się szybko, a następnie zwalnia, aby coraz bardziej zbliżać się do zera.

Równanie modelu regresji wykładniczej ma następującą postać:

y = ^abx

Złoto:

• y: zmienna odpowiedzi
• x: zmienna predykcyjna
• a, b: współczynniki regresji opisujące zależność pomiędzy x i y

Poniższy przykład pokazuje krok po kroku, jak przeprowadzić regresję wykładniczą w R.

Krok 1: Utwórz dane

Najpierw utwórzmy fałszywe dane dla dwóch zmiennych: x i y :

 x=1:20
y=c(1, 3, 5, 7, 9, 12, 15, 19, 23, 28, 33, 38, 44, 50, 56, 64, 73, 84, 97, 113)

Krok 2: Wizualizuj dane

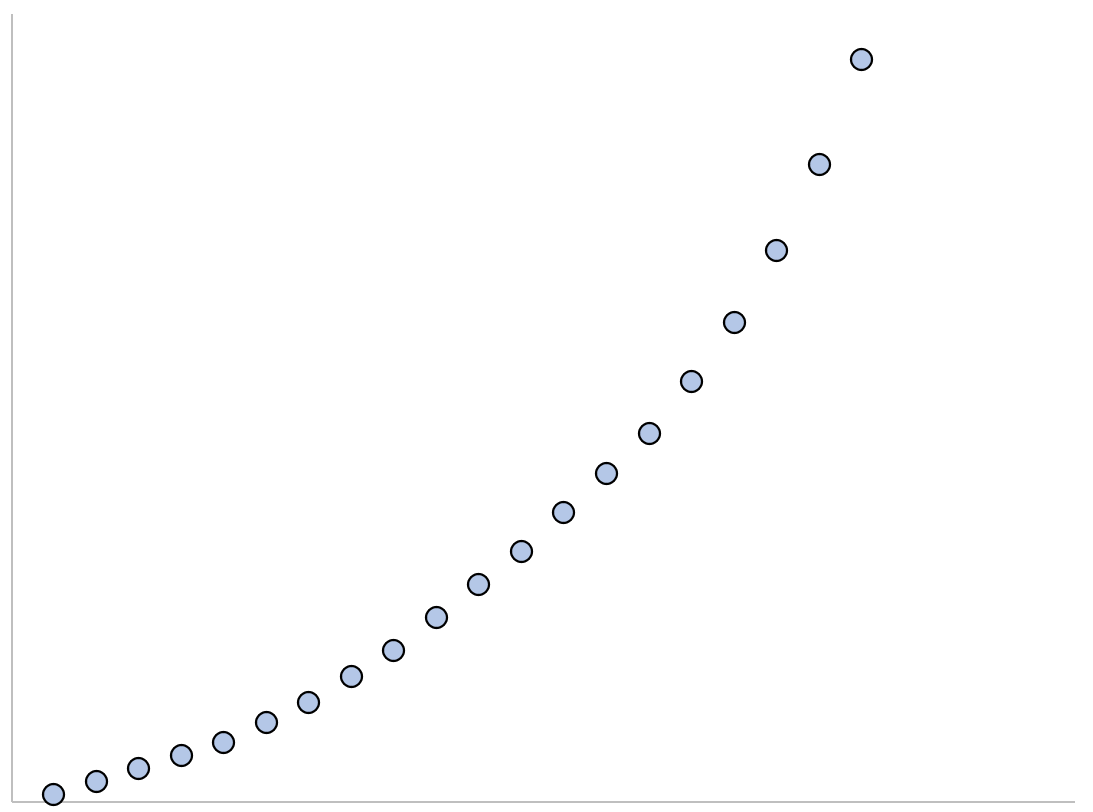
Następnie utwórzmy szybki wykres rozrzutu, aby zwizualizować relację między x i y :

 plot(x, y) 

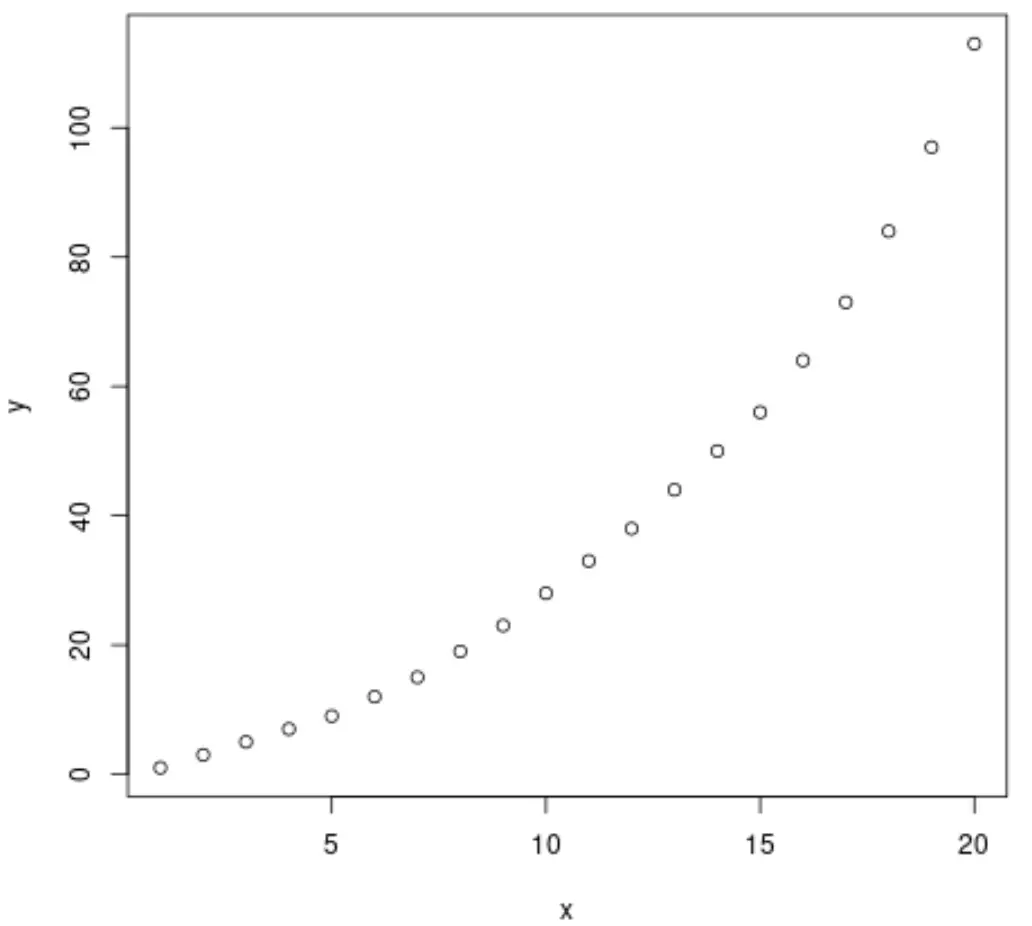
Z wykresu widać, że pomiędzy obiema zmiennymi występuje wyraźny wykładniczy wzór wzrostu.

Dlatego rozsądne wydaje się dopasowanie równania regresji wykładniczej w celu opisania zależności między zmiennymi.

Krok 3: Dopasuj model regresji wykładniczej

Następnie użyjemy funkcji lm() , aby dopasować model regresji wykładniczej, używając logarytmu naturalnego y jakozmiennej odpowiedzi i x jako zmiennej predykcyjnej:

 #fit the model
model <- lm( log (y) ~ x)

#view the output of the model
summary(model)

Call:
lm(formula = log(y) ~ x)

Residuals:
    Min 1Q Median 3Q Max 
-1.1858 -0.1768 0.1104 0.2720 0.3300 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.98166 0.17118 5.735 1.95e-05 ***
x 0.20410 0.01429 14.283 2.92e-11 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.3685 on 18 degrees of freedom
Multiple R-squared: 0.9189, Adjusted R-squared: 0.9144 
F-statistic: 204 on 1 and 18 DF, p-value: 2.917e-11

Ogólna wartość F modelu wynosi 204, a odpowiadająca jej wartość p jest wyjątkowo niska (2,917e-11), co wskazuje, że model jako całość jest użyteczny.

Korzystając ze współczynników z tabeli wyników, możemy zobaczyć, że dopasowane równanie regresji wykładniczej ma postać:

ln(y) = 0,9817 + 0,2041(x)

Stosując e do obu stron, możemy przepisać równanie w następujący sposób:

y = 2,6689 * ^1,2264x

Możemy użyć tego równania do przewidzenia zmiennej odpowiedzi y w oparciu o wartość zmiennej predykcyjnej x . Na przykład, jeśli x = 12, przewidywalibyśmy, że y wyniesie 30,897 :

y = 2,6689 * 1,2264 ¹² = 30,897

Premia: Skorzystaj z internetowego kalkulatora regresji wykładniczej, aby automatycznie obliczyć równanie regresji wykładniczej dla danego predyktora i zmiennej odpowiedzi.

Dodatkowe zasoby

Jak wykonać prostą regresję liniową w R
Jak wykonać wielokrotną regresję liniową w R
Jak wykonać regresję kwadratową w R
Jak wykonać regresję wielomianową w R