Jak przeprowadzić solidną regresję w r (krok po kroku)

Regresja solidna to metoda, którą możemy zastosować jako alternatywę dla zwykłej regresji metodą najmniejszych kwadratów, gdy w zbiorze danych, z którym pracujemy, występują wartości odstające lub wpływowe obserwacje .

Aby przeprowadzić solidną regresję w R, możemy użyć funkcji rlm() z pakietu MASS , która wykorzystuje następującą składnię:

Poniższy przykład pokazuje krok po kroku, jak przeprowadzić solidną regresję w języku R dla danego zbioru danych.

Krok 1: Utwórz dane

Najpierw utwórzmy fałszywy zbiór danych, z którym będziemy mogli pracować:

 #create data
df <- data. frame (x1=c(1, 3, 3, 4, 4, 6, 6, 8, 9, 3,
                      11, 16, 16, 18, 19, 20, 23, 23, 24, 25),
                 x2=c(7, 7, 4, 29, 13, 34, 17, 19, 20, 12,
                      25, 26, 26, 26, 27, 29, 30, 31, 31, 32),
                  y=c(17, 170, 19, 194, 24, 2, 25, 29, 30, 32,
                      44, 60, 61, 63, 63, 64, 61, 67, 59, 70))

#view first six rows of data
head(df)

  x1 x2 y
1 1 7 17
2 3 7 170
3 3 4 19
4 4 29 194
5 4 13 24
6 6 34 2

Krok 2: Wykonaj zwykłą regresję metodą najmniejszych kwadratów

Następnie dopasujmy zwykły model regresji metodą najmniejszych kwadratów i utwórzmy wykres reszt standaryzowanych .

W praktyce często za wartość odstającą uznajemy każdą standaryzowaną resztę, której wartość bezwzględna jest większa niż 3.

 #fit ordinary least squares regression model
ols <- lm(y~x1+x2, data=df)

#create plot of y-values vs. standardized residuals
plot(df$y, rstandard(ols), ylab=' Standardized Residuals ', xlab=' y ') 
abline(h= 0 ) 

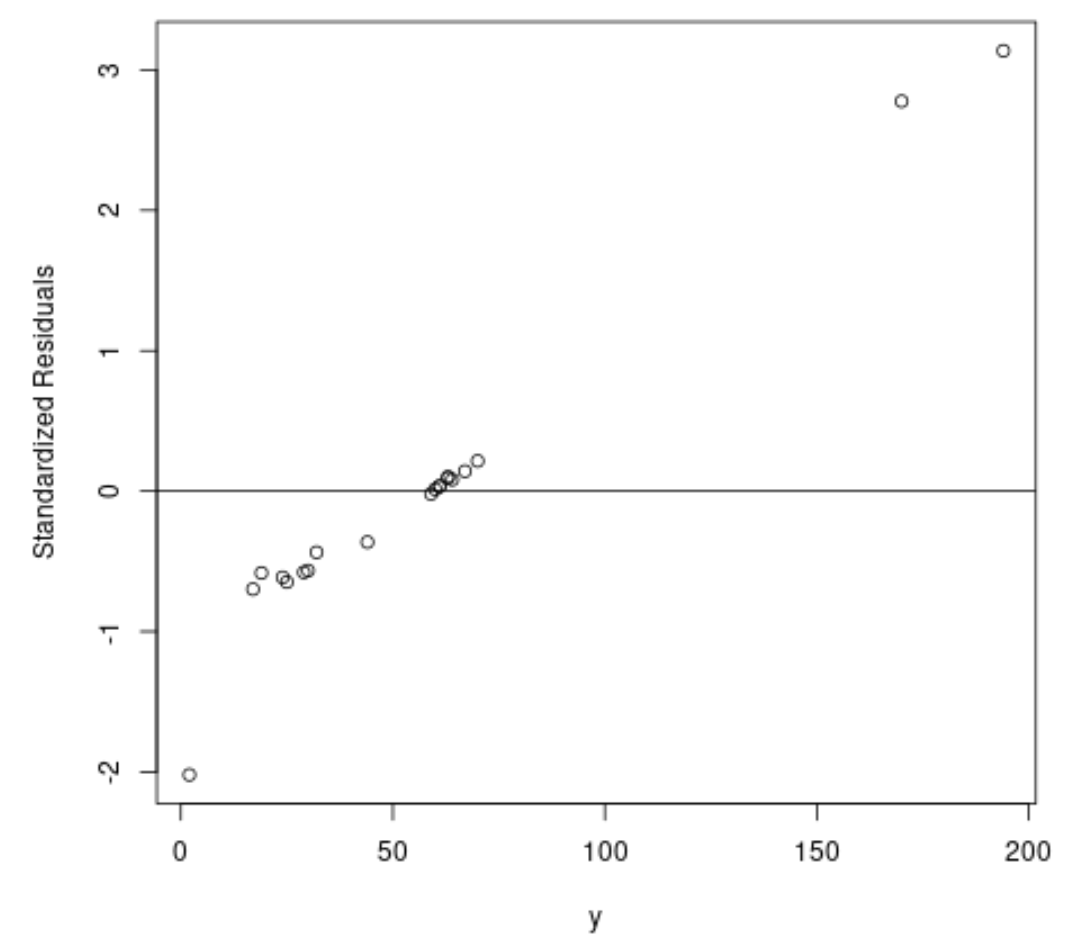
Z wykresu widać, że istnieją dwie obserwacje ze standardowymi resztami w okolicach 3.

Oznacza to, że w zbiorze danych znajdują się dwie potencjalne wartości odstające i dlatego zamiast tego możemy skorzystać z solidnej regresji.

Krok 3: Wykonaj solidną regresję

Następnie użyjmy funkcji rlm() , aby dopasować solidny model regresji:

 library (MASS)

#fit robust regression model
robust <- rlm(y~x1+x2, data=df)

Aby określić, czy ten solidny model regresji zapewnia lepsze dopasowanie do danych w porównaniu z modelem OLS, możemy obliczyć resztkowy błąd standardowy każdego modelu.

Resztowy błąd standardowy (RSE) to sposób pomiaru odchylenia standardowego reszt w modelu regresji. Im niższa wartość CSR, tym lepiej model jest w stanie dopasować dane.

Poniższy kod pokazuje, jak obliczyć RSE dla każdego modelu:

 #find residual standard error of ols model
summary(ols)$sigma

[1] 49.41848

#find residual standard error of ols model
summary(robust)$sigma

[1] 9.369349

Widzimy, że RSE solidnego modelu regresji jest znacznie niższy niż zwykłego modelu regresji metodą najmniejszych kwadratów, co mówi nam, że solidny model regresji zapewnia lepsze dopasowanie do danych.

Dodatkowe zasoby

Jak wykonać prostą regresję liniową w R
Jak wykonać wielokrotną regresję liniową w R
Jak wykonać regresję wielomianową w R