Jak wykonać test braku dopasowania w r (krok po kroku)

Test braku dopasowania służy do określenia, czy pełny model regresji zapewnia znacznie lepsze dopasowanie do zbioru danych niż zredukowana wersja modelu.

Załóżmy na przykład, że chcemy wykorzystać liczbę przepracowanych godzin do przewidywania wyników egzaminów studentów określonej uczelni. Możemy zdecydować się na dostosowanie następujących dwóch modeli regresji:

Model pełny: wynik = β ₀ + B ₁ (godziny) + B ₂ (godziny) ²

Model zredukowany: wynik = β ₀ + B ₁ (godziny)

Poniższy przykład pokazuje krok po kroku, jak przeprowadzić test braku dopasowania w R, aby określić, czy pełny model zapewnia znacznie lepsze dopasowanie niż model zredukowany.

Krok 1: Utwórz i wizualizuj zbiór danych

Najpierw użyjemy poniższego kodu, aby utworzyć zbiór danych zawierający liczbę przepracowanych godzin i wyniki egzaminów uzyskane dla 50 uczniów:

 #make this example reproducible
set. seeds (1)

#create dataset
df <- data. frame (hours = runif (50, 5, 15), score=50)
df$score = df$score + df$hours^3/150 + df$hours* runif (50, 1, 2)

#view first six rows of data
head(df)

      hours score
1 7.655087 64.30191
2 8.721239 70.65430
3 10.728534 73.66114
4 14.082078 86.14630
5 7.016819 59.81595
6 13.983897 83.60510

Następnie utworzymy wykres rozrzutu, aby zwizualizować związek między godzinami a wynikiem:

 #load ggplot2 visualization package
library (ggplot2)

#create scatterplot
ggplot(df, aes (x=hours, y=score)) +
  geom_point() 

Krok 2: Dopasuj dwa różne modele do zbioru danych

Następnie dopasujemy do zbioru danych dwa różne modele regresji:

 #fit full model
full <- lm(score ~ poly (hours,2), data=df)

#fit reduced model
reduced <- lm(score ~ hours, data=df)

Krok 3: Wykonaj test braku dopasowania

Następnie użyjemy polecenia anova() , aby przeprowadzić test braku dopasowania pomiędzy dwoma modelami:

 #lack of fit test
anova(full, reduced)

Analysis of Variance Table

Model 1: score ~ poly(hours, 2)
Model 2: score ~ hours
  Res.Df RSS Df Sum of Sq F Pr(>F)   
1 47 368.48                                
2 48 451.22 -1 -82.744 10.554 0.002144 **
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Statystyka testu F wynosi 10,554 , a odpowiadająca jej wartość p wynosi 0,002144 . Ponieważ ta wartość p jest mniejsza niż 0,05, możemy odrzucić hipotezę zerową testu i stwierdzić, że model pełny zapewnia statystycznie znacząco lepsze dopasowanie niż model zredukowany.

Krok 4: Wizualizuj ostateczny model

Wreszcie możemy wizualizować ostateczny model (pełny model) w porównaniu z oryginalnym zbiorem danych:

 ggplot(df, aes (x=hours, y=score)) + 
          geom_point() +
          stat_smooth(method=' lm ', formula = y ~ poly (x,2), size = 1) + 
          xlab(' Hours Studied ') +
          ylab(' Score ') 

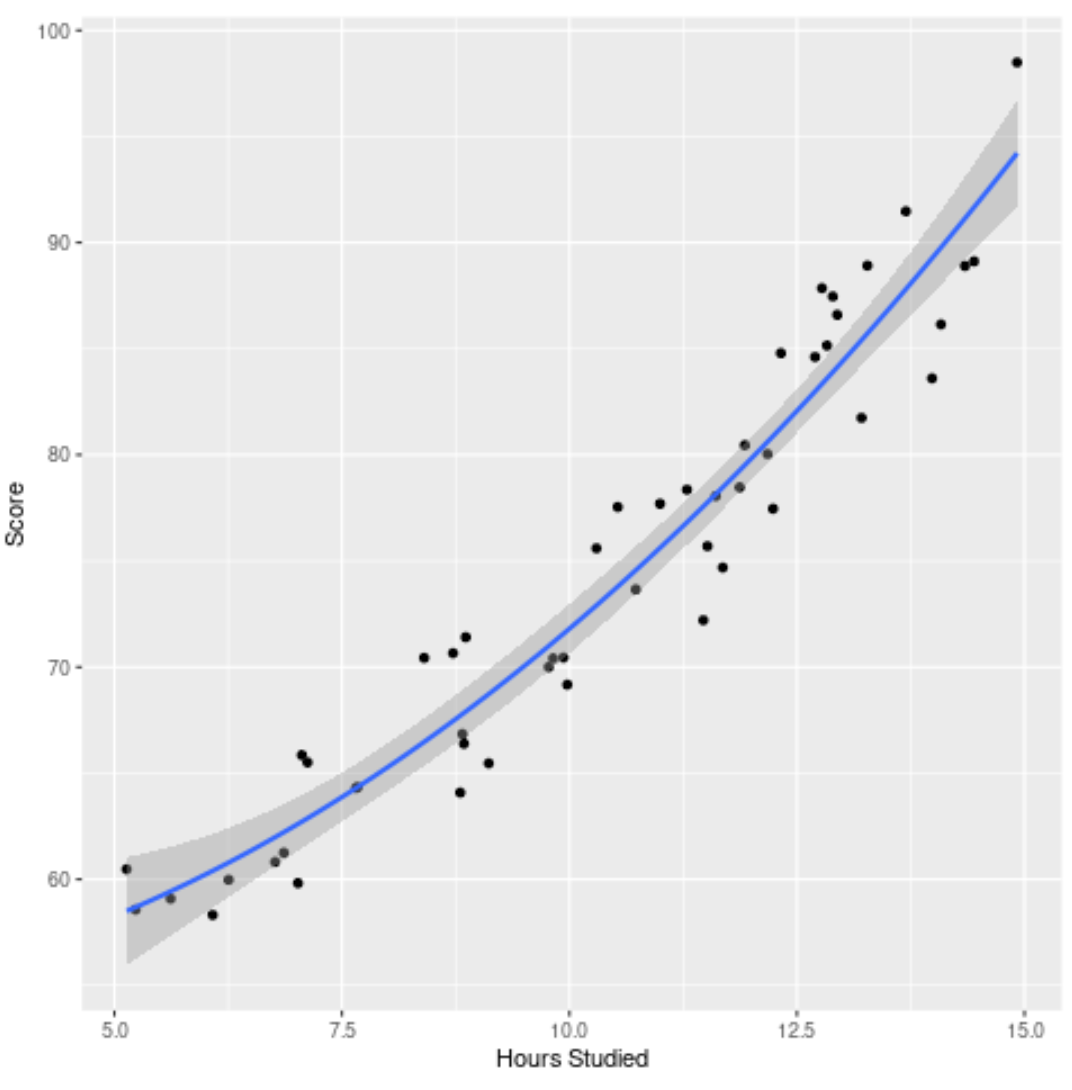
Widzimy, że krzywa modelu całkiem dobrze pasuje do danych.

Dodatkowe zasoby

Jak wykonać prostą regresję liniową w R
Jak wykonać wielokrotną regresję liniową w R
Jak wykonać regresję wielomianową w R