Jednokierunkowa anova: definicja, wzór i przykład
Jednoczynnikowa ANOVA („analiza wariancji”) porównuje średnie trzech lub więcej niezależnych grup w celu ustalenia, czy istnieje statystycznie istotna różnica między średnimi odpowiedniej populacji.
W tym samouczku wyjaśniono następujące kwestie:
- Motywacja do przeprowadzenia jednokierunkowej analizy ANOVA.
- Założenia, które należy spełnić, aby przeprowadzić jednokierunkową analizę wariancji.
- Proces przeprowadzania jednokierunkowej analizy ANOVA.
- Przykład wykonania jednokierunkowej analizy ANOVA.
Jednokierunkowa ANOVA: motywacja
Załóżmy, że chcemy wiedzieć, czy trzy różne programy przygotowujące do testów prowadzą do różnych średnich wyników na egzaminie wstępnym na studia. Ponieważ w całym kraju są miliony uczniów szkół średnich, obchodzenie każdego ucznia i umożliwienie mu skorzystania z jednego z programów przygotowujących do testu byłoby zbyt czasochłonne i kosztowne.
Zamiast tego moglibyśmy wybrać z populacji trzy losowe próbki składające się ze 100 uczniów i pozwolić każdej próbie skorzystać z jednego z trzech programów przygotowujących do testu w celu przygotowania się do egzaminu. Moglibyśmy wtedy rejestrować wyniki każdego ucznia po przystąpieniu do egzaminu.
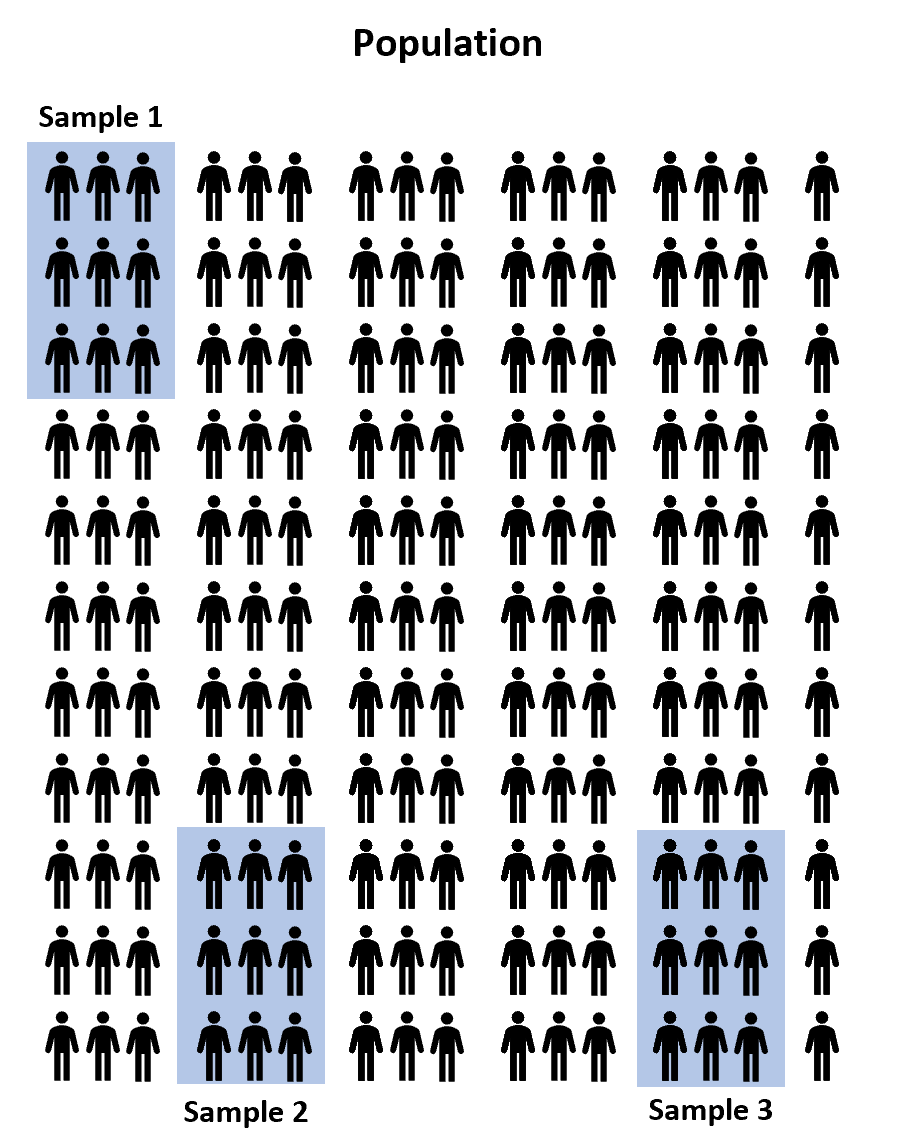
Jednak jest praktycznie gwarantowane, że średni wynik egzaminu pomiędzy trzema próbkami będzie przynajmniej trochę inny. Pytaniem jest, czy różnica ta jest istotna statystycznie . Na szczęście jednokierunkowa ANOVA pozwala nam odpowiedzieć na to pytanie.
Jednokierunkowa ANOVA: założenia
Aby wyniki jednokierunkowej analizy ANOVA były ważne, muszą zostać spełnione następujące założenia:
1. Normalność – każda próba została pobrana z populacji o rozkładzie normalnym.
2. Równe wariancje – wariancje populacji, z których pobierane są próbki, są równe. Aby przetestować tę hipotezę, możesz użyć testu Bartletta .
3. Niezależność – obserwacje w obrębie każdej grupy są od siebie niezależne, a obserwacje w obrębie grup uzyskano w drodze losowego doboru próby.
Przeczytaj ten artykuł , aby uzyskać więcej informacji na temat weryfikowania tych założeń.
Jednokierunkowa ANOVA: proces
Jednoczynnikowa ANOVA wykorzystuje następujące hipotezy zerowe i alternatywne:
- H 0 (hipoteza zerowa): μ 1 = μ 2 = μ 3 = … = μ k (wszystkie średnie populacji są równe)
- H 1 (hipoteza alternatywna): co najmniej jedna średnia populacji jest inna odpoczynek
Do przeprowadzenia jednoczynnikowej analizy ANOVA zazwyczaj będziesz używać oprogramowania statystycznego (takiego jak R, Excel, Stata, SPSS itp.), ponieważ ręczne wykonywanie tej analizy jest żmudne.
Niezależnie od używanego oprogramowania jako wynik otrzymasz następującą tabelę:
| Źródło | Suma kwadratów (SS) | zm | Średnie kwadraty (MS) | F | P |
|---|---|---|---|---|---|
| Leczenie | RSS | df r | MSR | MSR/MSE | F df r , df e |
| Błąd | ES | df e | MSE | ||
| Całkowity | BHP | df t |
Złoto:
- SSR: suma kwadratów regresji
- SSE: suma kwadratów błędu
- SST: całkowita suma kwadratów (SST = SSR + SSE)
- df r : stopnie swobody regresji (df r = k-1)
- df e : błędy stopni swobody (df e = nk)
- df t : całkowite stopnie swobody (df t = n-1)
- k: całkowita liczba grup
- n: całkowita liczba obserwacji
- MSR: regresja średniokwadratowa (MSR = SSR/df r )
- MSE: błąd średniokwadratowy (MSE = SSE/df e )
- F: Statystyka testowa F (F = MSR/MSE)
- p: Wartość p, która odpowiada F dfr, dfe
Jeśli wartość p jest mniejsza niż wybrany poziom istotności (np. 0,05), wówczas można odrzucić hipotezę zerową i stwierdzić, że przynajmniej jedna ze średnich populacji różni się od pozostałych.
Uwaga: Jeśli odrzucisz hipotezę zerową, oznacza to, że co najmniej jedna ze średnich populacji różni się od pozostałych, ale tabela ANOVA nie określa , które średnie populacji są różne. Aby to ustalić, należy przeprowadzić testy post hoc , zwane także testami „wielokrotnego porównania”.
Jednokierunkowa ANOVA: przykład
Załóżmy, że chcemy wiedzieć, czy trzy różne programy przygotowujące do testów prowadzą do różnych średnich wyników na danym egzaminie. Aby to przetestować, rekrutujemy 30 studentów do udziału w badaniu i dzielimy ich na trzy grupy.
Uczniowie w każdej grupie są losowo przydzielani do korzystania z jednego z trzech programów przygotowujących do testów przez kolejne trzy tygodnie w celu przygotowania się do egzaminu. Po trzech tygodniach wszyscy uczniowie przystępują do tego samego egzaminu.
Poniżej wyniki egzaminów dla poszczególnych grup:

Aby przeprowadzić jednokierunkową analizę ANOVA na tych danych, użyjemy jednokierunkowego kalkulatora statystycznej analizy ANOVA z następującymi danymi wejściowymi:

Z tabeli wyjściowej widzimy, że statystyka testu F wynosi 2,358 , a odpowiadająca jej wartość p wynosi 0,11385 .

Ponieważ ta wartość p jest nie mniejsza niż 0,05, nie możemy odrzucić hipotezy zerowej.
Oznacza to, że nie mamy wystarczających dowodów, aby stwierdzić, że istnieje statystycznie istotna różnica pomiędzy średnimi wynikami egzaminów trzech grup.
Dodatkowe zasoby
Poniższe artykuły wyjaśniają, jak przeprowadzić jednoczynnikową analizę ANOVA przy użyciu różnych programów statystycznych:
Jak wykonać jednokierunkową ANOVA w programie Excel
Jak wykonać jednokierunkową ANOVA w R
Jak wykonać jednokierunkową ANOVA w Pythonie
Jak wykonać jednokierunkową ANOVA w SAS
Jak wykonać jednokierunkową ANOVA w SPSS
Jak wykonać jednokierunkową ANOVA w Stata
Jak wykonać jednokierunkową ANOVA na kalkulatorze TI-84
Internetowy jednokierunkowy kalkulator ANOVA