T-score vs z-score: kiedy z nich korzystać?

Dwa terminy, które często mylą studentów na kursach statystyki, to wyniki t i wyniki z .

Obydwa są szeroko stosowane podczas testowania hipotez lub konstruowania przedziałów ufności , ale różnią się nieco.

Oto formuła dla każdego:

wynik t = ( x – μ) / (s/√ n )

Złoto:

• x : średnia próbki
• μ : średnia populacji
• s : odchylenie standardowe próbki
• n : Rozmiar próbki

wynik z = ( x – μ) / σ

Złoto:

• x : Surowa wartość danych
• μ : średnia populacji
• σ : odchylenie standardowe populacji

Na podstawie Twoich danych ten schemat blokowy pokazuje, kiedy należy używać każdego z nich:

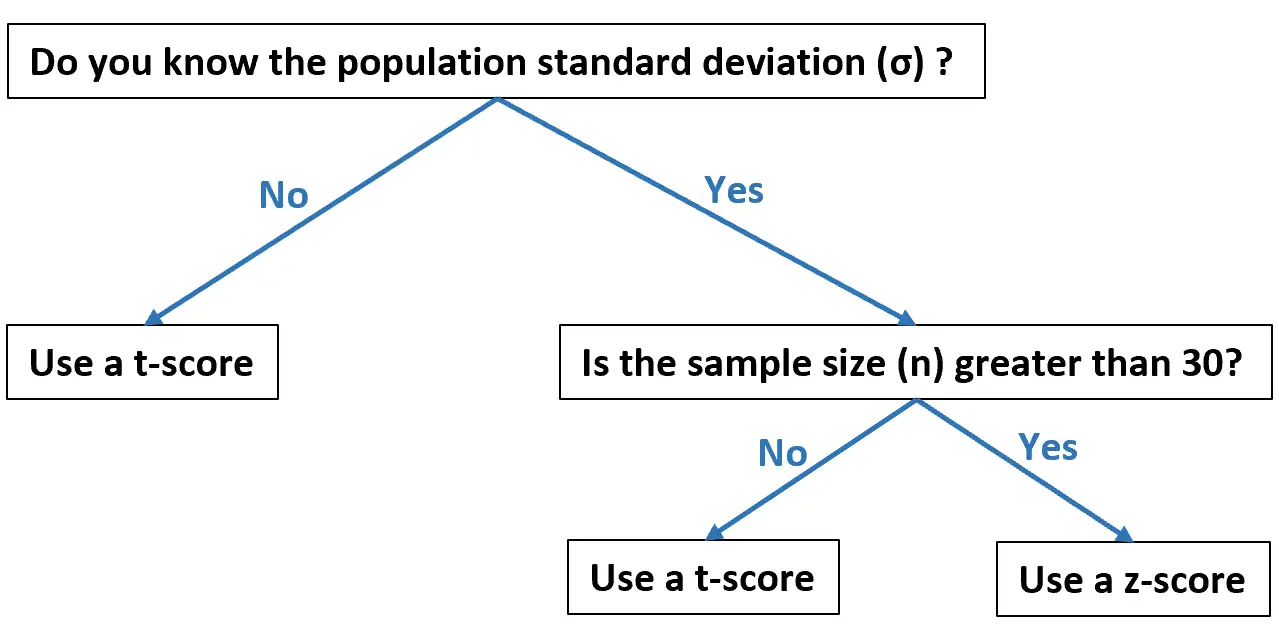
Poniższe przykłady pokazują, jak w praktyce obliczyć T-score i Z-score.

Przykład 1: Obliczanie wyniku T

Załóżmy, że restauracja przygotowuje hamburgery, których średnia waga wynosi μ = 0,25 funta.

Załóżmy, że pobieramy losową próbkę n = 20 hamburgerów i stwierdzamy, że średnia waga próbki wynosi x = 0,22 funta z odchyleniem standardowym s = 0,05 funta. Wykonaj test hipotezy, aby ustalić, czy rzeczywista średnia waga wszystkich hamburgerów produkowanych w tej restauracji wynosi 0,25 funta.

W tym przykładzie użylibyśmy wyniku T do sprawdzenia hipotezy, ponieważ żaden z poniższych dwóch warunków nie jest spełniony.

• Znane jest odchylenie standardowe populacji (σ). (w tym przykładzie nie podano σ)
• Wielkość próbki jest większa niż 30. (w tym przykładzie n=20)

Zatem obliczylibyśmy wynik t w następujący sposób:

• wynik t = ( x – μ) / (s/√ n )
• wynik t = (0,22 – 0,25) / (0,05 / √ 20 )
• wynik t = -2,68

Według kalkulatora wartości P , wartość p odpowiadająca temu wynikowi t wynosi 0,01481 .

Ponieważ ta wartość p jest mniejsza niż 0,05, mamy wystarczające dowody, aby stwierdzić, że średnia waga hamburgerów produkowanych w tej restauracji nie jest równa 0,25 funta.

Przykład 2: Obliczanie wyniku Z

Załóżmy, że firma produkuje baterie, których żywotność jest zgodna z rozkładem normalnym ze średnią μ = 20 godzin i odchyleniem standardowym σ = 5 godzin.

Załóżmy, że pobieramy losową próbkę n = 50 baterii i stwierdzamy, że średnia z próbki wynosi x = 21 godzin. Wykonaj test hipotezy, aby ustalić, czy rzeczywista średnia żywotność wszystkich akumulatorów produkowanych przez tę firmę wynosi 20 godzin.

W tym przykładzie użylibyśmy wyniku z do przeprowadzenia testu hipotezy, ponieważ spełnione są oba poniższe warunki:

• Znane jest odchylenie standardowe populacji (σ). (w tym przykładzie σ jest równe 5)
• Wielkość próby jest większa niż 30. (w tym przykładzie n=50)

Zatem obliczylibyśmy wynik Z w następujący sposób:

• wynik z = ( x – μ) / σ
• wynik z = (21 – 20) / 5
• wynik z = 0,2

Według kalkulatora wartości P, wartość p odpowiadająca temu wynikowi Z wynosi 0,84184 .

Ponieważ ta wartość p jest nie mniejsza niż 0,05, nie mamy wystarczających dowodów, aby stwierdzić, że średnia żywotność wszystkich akumulatorów produkowanych przez tę firmę różni się od 20 godzin.

Dodatkowe zasoby

Poniższe samouczki oferują więcej informacji na temat wyników T i Z:

Rozkład normalny a rozkład t: jaka jest różnica?
Jak czytać tablicę rozkładu t
Jak czytać tabelę Z