Co to jest zrównoważona dokładność? (definicja – przykład)

Zrównoważona dokładność to metryka, której możemy użyć do oceny wydajności modelu klasyfikacyjnego .

Oblicza się go w następujący sposób:

Zrównoważona dokładność = (czułość + swoistość) / 2

Złoto:

• Czułość : „prawdziwie pozytywny współczynnik” – procent pozytywnych przypadków, które model jest w stanie wykryć.
• Specyfika : „prawdziwie ujemny współczynnik” – odsetek przypadków negatywnych, jaki model jest w stanie wykryć.

Metryka ta jest szczególnie przydatna, gdy obie klasy są niezrównoważone, to znaczy, że jedna klasa pojawia się znacznie częściej niż druga.

Poniższy przykład pokazuje, jak w praktyce obliczyć zrównoważoną dokładność i pokazuje, dlaczego jest to tak przydatny miernik.

Przykład: Obliczanie zrównoważonej precyzji

Załóżmy, że analityk sportowy używa modelu regresji logistycznej do przewidzenia, czy 400 różnych koszykarzy z college’u zostanie powołanych do NBA.

Poniższa macierz zamieszania podsumowuje przewidywania dokonane przez model:

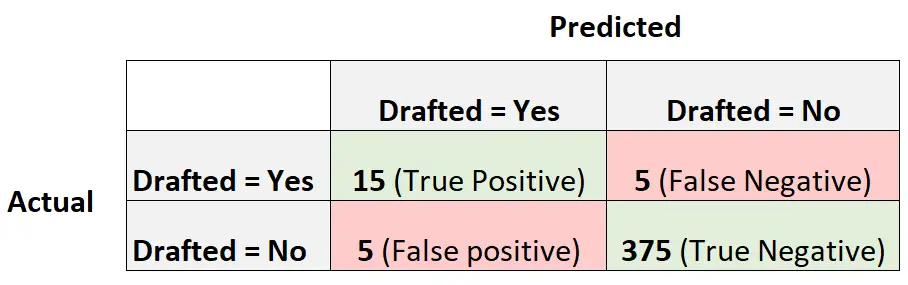
Aby obliczyć zrównoważoną dokładność modelu, najpierw obliczymy czułość i swoistość:

• Czułość : „prawdziwie dodatni współczynnik” = 15 / (15 + 5) = 0,75
• Specyfika : „Współczynnik prawdziwie ujemny” = 375 / (375 + 5) = 0,9868

Następnie możemy obliczyć zrównoważoną precyzję w następujący sposób:

• Zrównoważona dokładność = (czułość + swoistość) / 2
• Zrównoważona dokładność = (0,75 + 9868) / 2
• Zrównoważona dokładność = 0,8684

Zrównoważona dokładność modelu wynosi 0,8684 .

Należy zauważyć, że im precyzja zrównoważona jest bliższa 1, tym lepiej model jest w stanie poprawnie klasyfikować obserwacje.

W tym przykładzie zrównoważona dokładność jest dość wysoka, co mówi nam, że model regresji logistycznej bardzo dobrze radzi sobie z przewidywaniem, czy gracze z college’u zostaną powołani do NBA.

W tym scenariuszu, ponieważ klasy są bardzo niezrównoważone (wybrano 20 graczy, a 380 nie), zrównoważona dokładność daje nam bardziej realistyczny obraz wydajności modelu w porównaniu z ogólną miarą dokładności.

Na przykład obliczylibyśmy dokładność modelu w następujący sposób:

• Dokładność = (TP + TN) / (TP + TN + FP + FN)
• Dokładność = (15 + 375) / (15 + 375 + 5 + 5)
• Dokładność = 0,975

Dokładność modelu wynosi 0,975 , co wydaje się niezwykle wysokie.

Rozważmy jednak model, który po prostu przewiduje, że każdy gracz nie zostanie wybrany. Miałby dokładność 380/400 = 0,95 . To tylko nieznacznie mniej niż dokładność naszego modelu.

Zrównoważony wynik dokładności wynoszący 0,8684 daje nam lepsze wyobrażenie o zdolności modelu do przewidywania obu klas.

Innymi słowy, daje nam to lepszy pogląd na zdolność modelu do przewidywania, którzy gracze nie zostaną wybrani , a którzy to zrobią.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak utworzyć macierz zamieszania w różnych programach statystycznych:

Jak utworzyć macierz zamieszania w programie Excel
Jak utworzyć macierz zamieszania w R
Jak utworzyć macierz zamieszania w Pythonie