Écart semi-interquartile

Cet article explique ce qu’est l’intervalle semi-interquartile dans les statistiques. Ainsi, vous trouverez comment calculer l’intervalle semi-interquartile, un exercice résolu et, en plus, un calculateur en ligne pour calculer l’intervalle semi-interquartile de n’importe quel échantillon de données.

Qu’est-ce que l’intervalle semi-interquartile ?

L’ intervalle semi-interquartile (ou intervalle semi-interquartile ) correspond à la moitié de la différence entre le premier et le troisième quartile. Par conséquent, pour calculer l’intervalle semi-interquartile, vous devez soustraire le troisième quartile moins le premier quartile, puis diviser par deux.

L’intervalle semi-interquartile est une mesure de dispersion qui indique la variabilité des valeurs centrales. Ainsi, plus l’intervalle semi-interquartile d’un ensemble de données est grand, plus les valeurs au centre sont dispersées les unes par rapport aux autres.

L’une des caractéristiques de l’intervalle semi-interquartile est qu’il s’agit d’un paramètre statistique robuste, de sorte que les observations aberrantes n’affectent pas l’intervalle semi-interquartile.

Ainsi, l’intervalle semi-interquartile est une mesure de dispersion similaire à l’intervalle statistique, puisqu’il indique la variabilité d’un ensemble de données en soustrayant deux valeurs quartiles. Cependant, la plage statistique est calculée légèrement différemment.

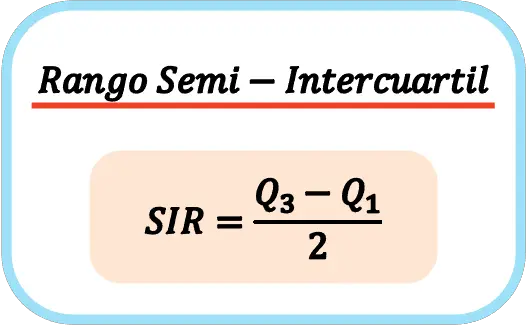
Formule d’intervalle semi-interquartile

L’écart semi-interquartile est égal à la différence entre le troisième quartile et le premier quartile divisée par deux. Par conséquent, pour calculer l’intervalle semi-interquartile, vous devez d’abord trouver le premier et le troisième quartile, puis les soustraire et enfin diviser le résultat de la soustraction par deux.

Ainsi, la formule pour calculer l’intervalle semi-interquartile est la suivante :

Vous pouvez utiliser la calculatrice ci-dessous pour calculer l’intervalle semi-interquartile de n’importe quel ensemble de données.

Généralement, pour représenter l’intervalle semi-interquartile, l’acronyme SIR ( Semi Intquartile Range ) est généralement utilisé comme symbole de cette mesure statistique.

En bref, l’intervalle semi-interquartile correspond à la moitié de l’ intervalle interquartile .

Exemple de calcul de l’intervalle semi-interquartile

Après avoir vu la définition de l’intervalle semi-interquartile et sa formule, vous trouverez ci-dessous un exemple concret pour expliquer clairement comment l’intervalle semi-interquartile est calculé.

• Nous souhaitons analyser statistiquement si c’est une bonne idée d’investir dans une entreprise. Pour ce faire, nous avons collecté des données sur le cours de l’action de cette entreprise au cours des 15 derniers mois. Dans le tableau suivant, vous pouvez voir les données observées classées du plus bas au plus élevé. Calculez l’intervalle semi-interquartile de cet ensemble de données.

Comme expliqué dans la section ci-dessus, pour trouver l’intervalle semi-interquartile, nous devons d’abord déterminer les premier et troisième quartiles.

Le premier quartile est la médiane de la première moitié des valeurs, qui correspond à la valeur 8,95 €/action.

En revanche, le troisième quartile est la valeur intermédiaire de la seconde moitié des valeurs, soit 9,83 €/action.

Une fois que l’on connaît les valeurs du premier et du troisième quartiles, il suffit d’appliquer la formule de l’intervalle semi-interquartile pour trouver sa valeur :

Calculateur d’intervalle semi-interquartile

Entrez un ensemble de données statistiques dans le calculateur en ligne suivant pour calculer son intervalle semi-interquartile. Les données doivent être séparées par un espace et saisies en utilisant le point comme séparateur décimal.