Polygone de fréquence

Cet article explique en quoi consiste un polygone de fréquence et à quoi il sert. De plus, vous découvrirez quels sont les différents types de polygones de fréquence et un exemple de chacun.

Qu’est-ce qu’un polygone de fréquence ?

Un polygone de fréquence est un type de graphique statistique dans lequel l’ensemble de données est représenté par des points et relié par des lignes.

En statistiques, le polygone de fréquence est généralement utilisé pour représenter une série chronologique. Car ce type de diagrammes est très utile pour analyser l’évolution des données.

Le polygone de fréquence peut être réalisé en joignant les extrémités des barres d’un graphique à barres ou d’un histogramme. Ci-dessous, nous verrons comment cela se fait.

Comment créer un polygone de fréquence

Les étapes pour créer un polygone de fréquence sont les suivantes :

1. Dessinez l’axe horizontal et l’axe vertical du polygone de fréquence et créez l’échelle afin de pouvoir ensuite représenter les données sur le graphique.
2. Représentez les paires de données sous forme de points sur le graphique.
3. Joignez les points consécutifs sur le graphique à l’aide d’une ligne.

Exemple de polygone de fréquence

Pour que vous puissiez voir exactement comment construire un polygone de fréquence, vous trouverez ci-dessous un exemple expliqué.

• Le tableau de données suivant a compilé la valeur des actions des 10 dernières années d’une société cotée en bourse. Représentez graphiquement les données à l’aide d’un polygone de fréquence.

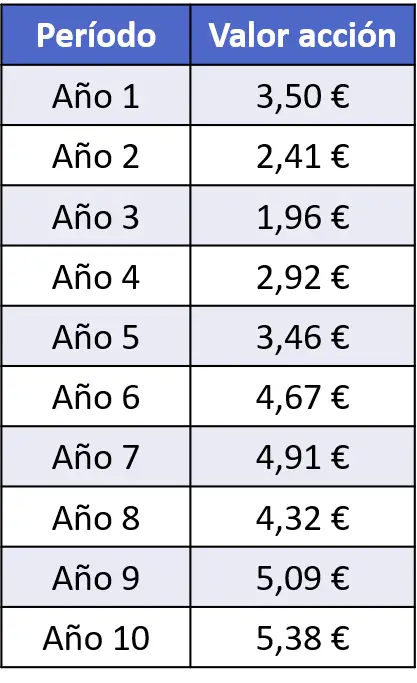
Tout d’abord, il faut représenter les axes du polygone de fréquence. Sur l’axe horizontal nous mettrons les périodes et sur l’axe vertical les cours des actions :

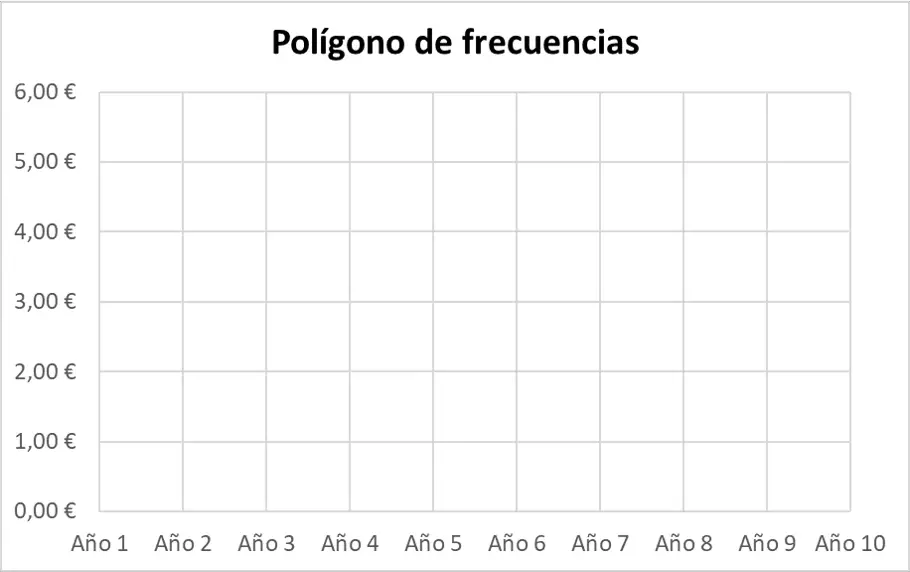
Deuxièmement, nous représentons l’ensemble de données statistiques avec des points. N’oubliez pas que chaque point est représenté sur le graphique là où se croisent les deux lignes imaginaires issues de leurs valeurs correspondantes sur les axes.

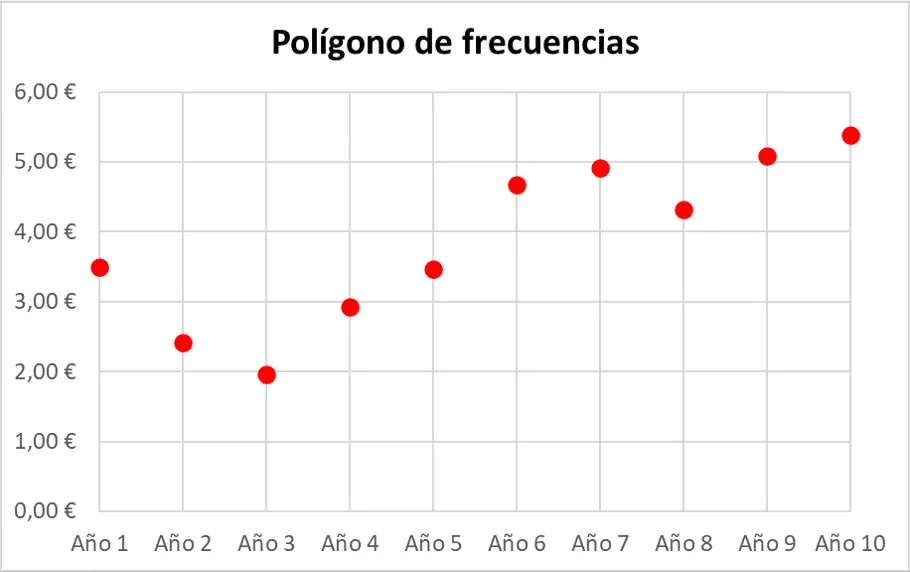
Pour finir, il suffit de joindre les points consécutifs par une ligne droite, formant une ligne continue pour tout le polygone fréquentiel.

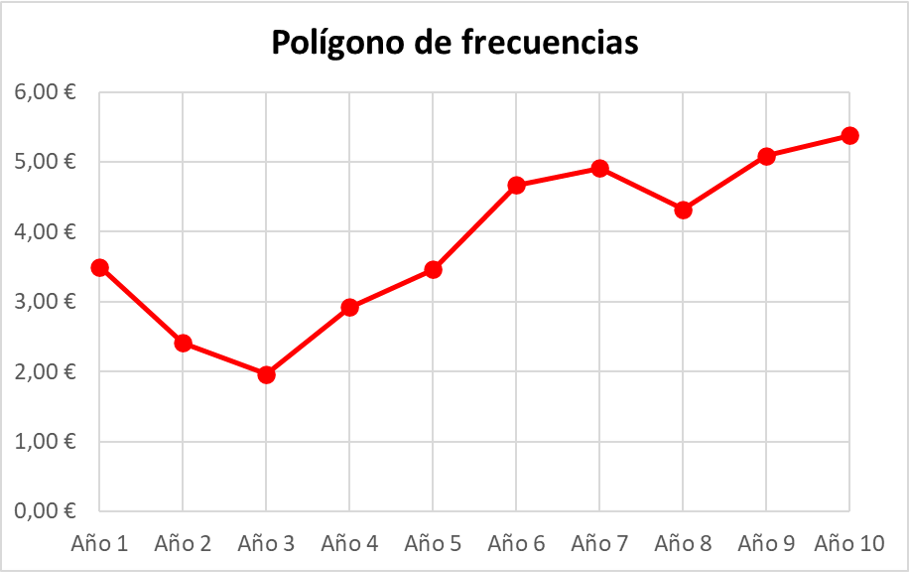
Dans ce cas, les fréquences absolues ont été représentées dans le polygone de fréquences, mais les fréquences relatives (ou en pourcentage) auraient également pu être représentées.

Polygone de fréquence pour les données groupées

Nous venons de voir comment est réalisé un polygone de fréquence lorsque la variable est discrète, mais un polygone de fréquence peut également être réalisé avec des variables continues, c’est-à-dire lorsque les données sont regroupées en intervalles. Ci-dessous vous pouvez voir un exemple de ce type résolu.

• La taille d’un échantillon de 50 personnes a été mesurée et les données ont été enregistrées dans le tableau de fréquence suivant. Représentez graphiquement les données à l’aide d’un polygone de fréquence.

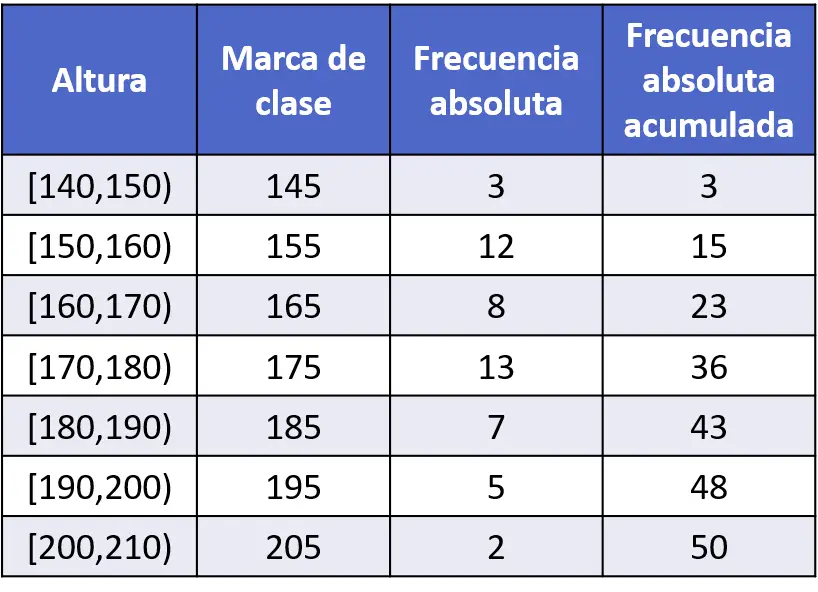
Puisque les données sont regroupées par intervalles, les points du polygone de fréquence doivent être tracés au niveau de la marque de classe de chaque intervalle, c’est-à-dire au milieu des extrémités de l’intervalle.

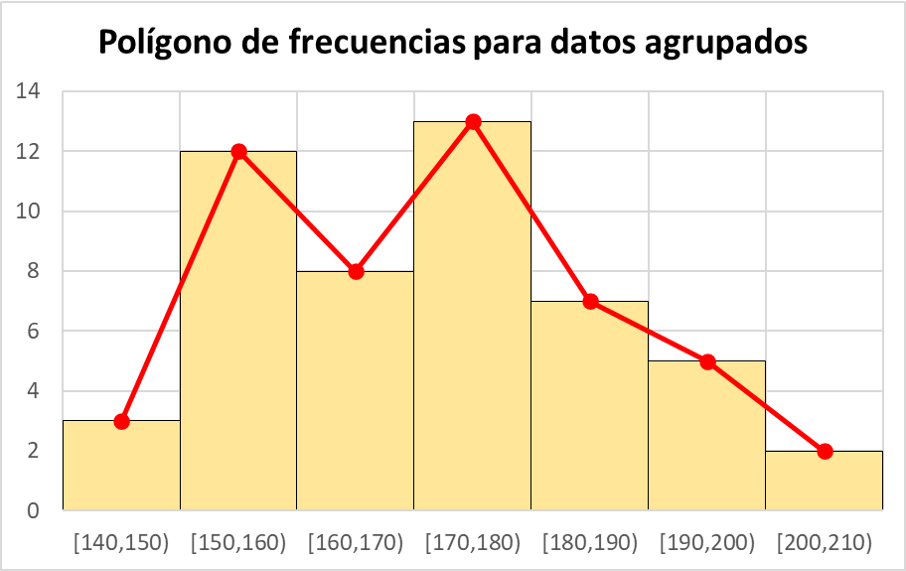
Comme le montre le diagramme, lorsque les données sont regroupées, le polygone de fréquence peut être combiné avec un histogramme. En fait, si vous faites d’abord l’histogramme, pour tracer le polygone de fréquence il vous suffit de joindre les milieux de chaque barre rectangulaire de l’histogramme.

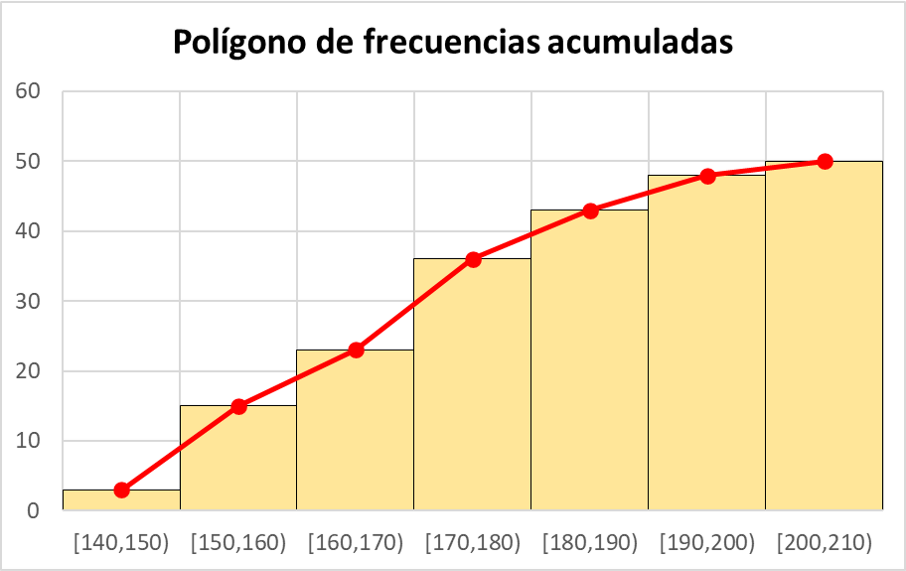
Polygone de fréquence cumulée

En statistiques, le polygone de fréquence est également utilisé pour représenter les fréquences cumulées. Calculez simplement d’abord les fréquences cumulées de l’ensemble de données, puis utilisez les fréquences cumulées au lieu des fréquences absolues pour représenter les points du polygone de fréquence.

N’oubliez pas que la fréquence absolue cumulée est calculée en additionnant toutes les fréquences absolues précédentes plus la fréquence absolue de l’intervalle lui-même.

À titre d’exemple, vous pouvez voir ci-dessous le polygone de fréquence absolue cumulée de l’ensemble de données de l’exercice précédent :