Population signifie

Par Pr Amélia Rodriguez août 3, 2023 Statistiques 0 commentaire

Cet article explique ce que signifie la population dans les statistiques. De même, vous découvrirez quelle est la formule pour la moyenne de la population, comment est calculé l’intervalle de confiance de la moyenne de la population et, en outre, quelle est la différence entre la moyenne de la population et la moyenne de l’échantillon.

Quelle est la moyenne de la population ?

La moyenne de population est la moyenne arithmétique de tous les éléments de la population statistique. Par conséquent, pour calculer la moyenne de la population, toutes les valeurs de la population doivent être additionnées puis divisées par le nombre total d’éléments de la population.

Le symbole de la moyenne de la population est la lettre grecque μ.

De même, la moyenne de la population peut également être définie comme la valeur attendue de la variable qui représente une population.

Comment calculer la moyenne de la population

Une fois que nous avons vu la définition de la moyenne d’une population, voyons comment la moyenne d’une population est calculée pour mieux comprendre sa signification.

Si toutes les valeurs de la population statistique sont connues, la formule de la moyenne arithmétique doit simplement être appliquée pour calculer la moyenne de la population. Donc, dans ce cas, pour calculer la moyenne de la population, nous devons additionner toutes les valeurs de la population puis diviser par le nombre total de données.

Ainsi, si l’on connaît la valeur de tous les éléments de la population, la formule pour calculer la moyenne de la population est la suivante :

$\displaystyle\mu=\frac{\displaystyle \sum_{i=1}^N x_i}{N}=\frac{x_1+x_2+\dots +x_N}{N}$

➤ Voir : Exemple de calcul de la moyenne arithmétique

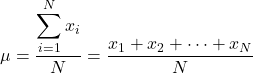
Cependant, en général, toutes les valeurs de la population ne sont pas connues, donc normalement la valeur de la moyenne de la population est estimée par intervalles .

Intervalle de confiance pour la moyenne de la population

En pratique, il est impossible d’étudier tous les individus d’une population, c’est pourquoi un échantillon aléatoire de la population est normalement choisi et, sur la base de ses valeurs, une approximation de la valeur de la moyenne de la population est effectuée. Plus précisément, on calcule un intervalle dans lequel la moyenne de la population entière est très susceptible de se trouver ; cet intervalle est appelé intervalle de confiance pour la moyenne de la population.

L’ intervalle de confiance pour la moyenne de la population est calculé en ajoutant et en soustrayant de la moyenne de l’échantillon la valeur de Z _α/2 multipliée par l’écart type (σ) et divisée par la racine carrée de la taille de l’échantillon (n). Par conséquent, la formule pour calculer l’intervalle de confiance pour la moyenne de la population est la suivante :

$\displaystyle \left(\overline{x}-z_{\alpha/2}\cdot \frac{\sigma}{\sqrt{n}} \ , \ \overline{x}+z_{\alpha/2}\cdot \frac{\sigma}{\sqrt{n}} \right)$

La formule ci-dessus est utilisée lorsque la variance de la population est connue. Cependant, si la variance de la population est inconnue, ce qui est le cas le plus courant, l’intervalle de confiance pour la moyenne est calculé à l’aide de la formule suivante :

$\displaystyle \left(\overline{x}-t_{\alpha/2}\cdot \frac{s}{\sqrt{n}} \ , \ \overline{x}+t_{\alpha/2}\cdot \frac{s}{\sqrt{n}} \right)$

Où:

$\overline{x}$ est la moyenne de l’échantillon.
$t_{\alpha/2}$ est la valeur de la distribution t de Student de n-1 degrés de liberté avec une probabilité α/2. Pour des échantillons de grande taille et un niveau de confiance de 95 %, il est généralement proche de 1,96 et pour un niveau de confiance de 99 %, il est généralement proche de 2,576.
$s$ est l’écart type de l’échantillon.
$n$ est la taille de l’échantillon.

➤ Voir : Exemple de calcul de l’intervalle de confiance pour la moyenne de la population

Moyenne de la population et moyenne de l’échantillon

Enfin, en résumé, nous passerons en revue les différences entre la moyenne de la population et la moyenne de l’échantillon afin que ces deux concepts statistiques soient clairs.

La différence entre la moyenne de la population et la moyenne de l’échantillon est la plage de valeurs sur laquelle la moyenne est calculée. La moyenne de la population est la moyenne de l’ensemble de la population statistique, tandis que la moyenne de l’échantillon est la moyenne d’un échantillon de la population.

De plus, pour différencier la moyenne de la population de la moyenne de l’échantillon, elles sont représentées par des symboles différents. Le symbole de la moyenne de la population est

$\mu$ , en revanche, le symbole de la moyenne de l’échantillon est $\overline{x}$ .

$\begin{array}{c}\mu =\text{Media poblacional}\\[2ex]\overline{x} = \text{Media muestral}\end{array}$

Si vous avez encore des doutes sur les différences entre ces deux types de moyennes ou souhaitez en savoir plus sur le calcul de la moyenne d’un échantillon, vous pouvez consulter l’article suivant :

➤ Voir : Quelle est la moyenne de l’échantillon ?

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus