Population statistique

Dans cet article, nous expliquons ce qu’est la population statistique. Vous trouverez plusieurs exemples de populations statistiques, les différents types de populations qui existent et enfin quelle est la différence entre population et échantillon en statistique.

Qu’est-ce qu’une population statistique ?

En statistique, une population est un ensemble d’éléments présentant des caractéristiques similaires sur lesquels une étude statistique est destinée à être réalisée.

On peut désigner ce concept par le terme population statistique ou simplement par population, de manière interchangeable.

Ensuite, la taille de la population , également appelée taille de la population, est constituée du nombre total d’éléments du groupe que vous souhaitez étudier.

Exemples de population statistique

Compte tenu de la définition de population statistique, nous allons voir plusieurs exemples de populations pour mieux comprendre sa signification.

Par exemple, lorsqu’on fait une étude sur les notes obtenues par les élèves d’une classe au cours d’une année, les élèves de cette classe constituent la population statistique de l’étude.

Autre exemple, si vous souhaitez faire une analyse statistique de la qualité des pièces produites dans une usine pendant une période donnée, toutes les pièces produites par cette usine pendant cette période constitueront la population étudiée.

Enfin, les habitants d’un territoire sont également une population statistique lorsque des statistiques sont réalisées sur ledit territoire, comme par exemple lorsque l’on calcule l’espérance de vie d’un pays, les habitants de ce pays représentent la population statistique de l’étude.

Types de population statistique

Il existe deux types de populations statistiques :

• Population statistique finie : population dont le nombre d’éléments est fini, c’est-à-dire qu’ils peuvent être comptés.
• Population statistique infinie : population dont le nombre d’éléments est infini, c’est-à-dire qui n’a pas de fin.

Par exemple, le nombre de voitures qui circulent sur une route au cours d’une journée constitue une population finie puisque, même s’il s’agit d’un nombre très important, il est dénombrable. Au lieu de cela, le nombre de planètes dans l’univers constitue une population infinie car toutes les planètes n’ont pas encore été découvertes et ne peuvent donc pas être comptées.

Vous devez garder à l’esprit qu’il existe de nombreuses façons de regrouper les types de populations statistiques, elles peuvent également être divisées en populations qualitatives et populations quantitatives en fonction de leur variable. Mais normalement, une grande classification est faite entre populations finies et populations infinies.

Population statistique et échantillon

Enfin, nous allons voir en quoi les notions de population et d’échantillon diffèrent en statistique, puisque ce sont deux termes qui vont généralement de pair.

En statistique, la différence entre population et échantillon est la proportion par rapport au nombre total d’éléments de l’étude. La population statistique est l’ensemble des éléments sur lesquels l’étude est réalisée, cependant, l’échantillon statistique fait partie de tous les éléments de l’étude.

La taille d’un échantillon sera donc toujours inférieure ou égale à la taille d’une population.

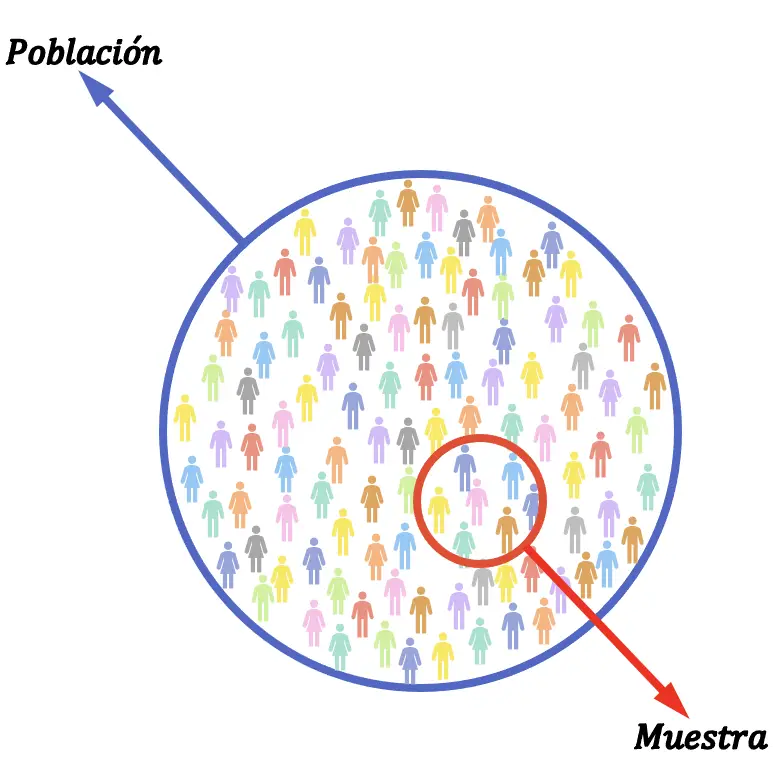
L’échantillon statistique peut également être appelé un sous-ensemble de la population.

Normalement, pour étudier statistiquement une population, les données ne sont pas prélevées sur chaque élément de la population, mais plutôt un échantillon représentatif est choisi, l’étude est réalisée sur l’échantillon, puis les conclusions sont extrapolées à l’ensemble de la population.

Par exemple, lorsque vous souhaitez faire une étude de marché, vous ne demandez pas à toutes les personnes intéressées par votre produit, vous faites seulement une enquête sur une partie et avec les données collectées vous étudiez le marché.

Il convient de noter que la taille de l’échantillon (taille de l’échantillon) d’une étude statistique n’est pas triviale à déterminer, car plus la taille de l’échantillon est grande, mieux elle représente la population, mais plus la taille de l’échantillon est grande, plus l’analyse sera compliquée. et il faudra donc davantage de ressources et plus d’argent.