Pourquoi l’écart type est-il important ? (Explication + Exemples)

L’ écart type est utilisé pour mesurer la répartition des valeurs dans un échantillon.

Nous pouvons utiliser la formule suivante pour calculer l’écart type d’un échantillon donné :

√ Σ(x _je – x _barre ) ² / (n-1)

où:

• Σ : Un symbole qui signifie « somme »
• x _i : la ^ième valeur de l’échantillon
• x _bar : La moyenne de l’échantillon
• n : La taille de l’échantillon

Plus la valeur de l’écart type est élevée, plus les valeurs sont dispersées dans un échantillon. À l’inverse, plus la valeur de l’écart type est faible, plus les valeurs sont étroitement regroupées.

Une question que les étudiants se posent souvent est la suivante : Pourquoi l’écart type est-il important ?

La réponse : l’écart type est important car il nous indique la répartition des valeurs dans un ensemble de données donné.

Chaque fois que nous analysons un ensemble de données, nous souhaitons trouver les métriques suivantes :

• Le centre de l’ensemble de données . La façon la plus courante de mesurer le « centre » consiste à utiliser la moyenne et la médiane.
• La répartition des valeurs dans l’ensemble de données . La façon la plus courante de mesurer la propagation consiste à utiliser l’écart type.

En sachant où se trouve le centre et quelle est la répartition des valeurs, nous pouvons bien comprendre la distribution des valeurs dans n’importe quel ensemble de données.

Les exemples suivants illustrent l’importance de l’écart type dans la pratique.

Exemple 1 : Répartition des salaires

Supposons que le salaire moyen dans l’entreprise A soit de 80 000 $ et que l’écart type soit de 20 000 $. Étant donné que l’écart type est si important, rien ne garantit que vous serez payé près de 80 000 $ par an si vous travaillez dans cette entreprise, car il existe une telle variation dans les salaires.

À l’inverse, supposons que le salaire moyen dans l’entreprise B soit également de 80 000 $, mais que l’écart type ne soit que de 4 000 $. Étant donné que cet écart type est si petit, vous pouvez être sûr que vous serez payé près de 80 000 $ car il y a très peu de variation dans les salaires.

Si nous créions un boxplot pour visualiser la répartition des salaires dans ces deux entreprises, cela pourrait ressembler à ceci :

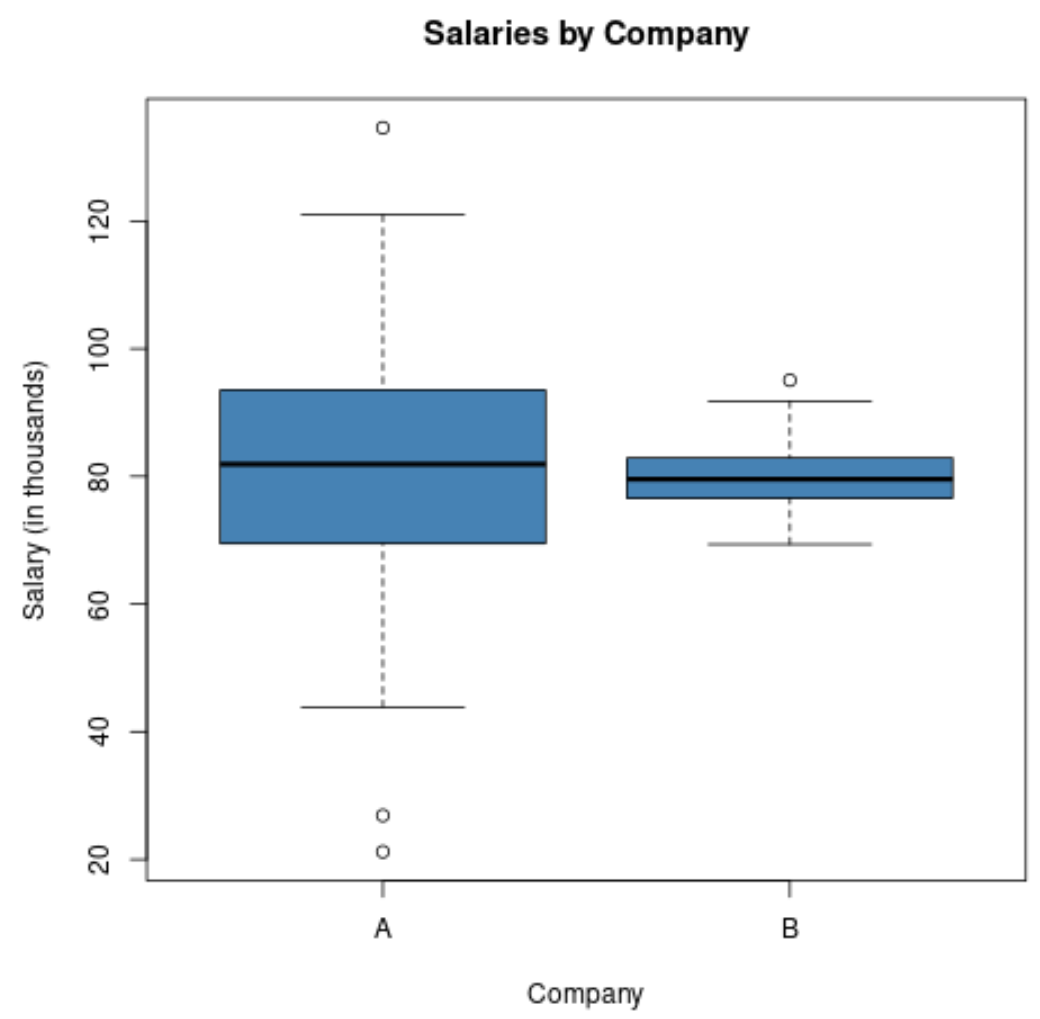
Notez que la longueur du boxplot pour l’entreprise A est d’autant plus grande que l’écart type des salaires est bien plus élevé.

Les deux entreprises ont le même salaire moyen, mais l’écart des salaires est beaucoup plus élevé dans l’entreprise A.

Exemple 2 : Répartition des prix des logements

Supposons que le prix moyen d’un logement dans le quartier A soit de 250 000 $ et que l’écart type soit de 50 000 $. Étant donné que l’écart type est assez important, cela signifie que certains prix de l’immobilier seront bien supérieurs à 250 000 dollars et que d’autres seront bien inférieurs. Si vous regardez une maison donnée dans ce quartier, rien ne garantit que le prix sera proche de la moyenne.

À l’inverse, supposons que le prix moyen de l’immobilier dans le quartier B soit également de 250 000 $, mais que l’écart type ne soit que de 10 000 $. Étant donné que cet écart type est assez faible, vous pouvez être sûr que n’importe quelle maison que vous regardez dans le quartier sera probablement proche de ce prix.

Si nous créions un boxplot pour visualiser la répartition des prix de l’immobilier dans ces deux quartiers, cela pourrait ressembler à ceci :

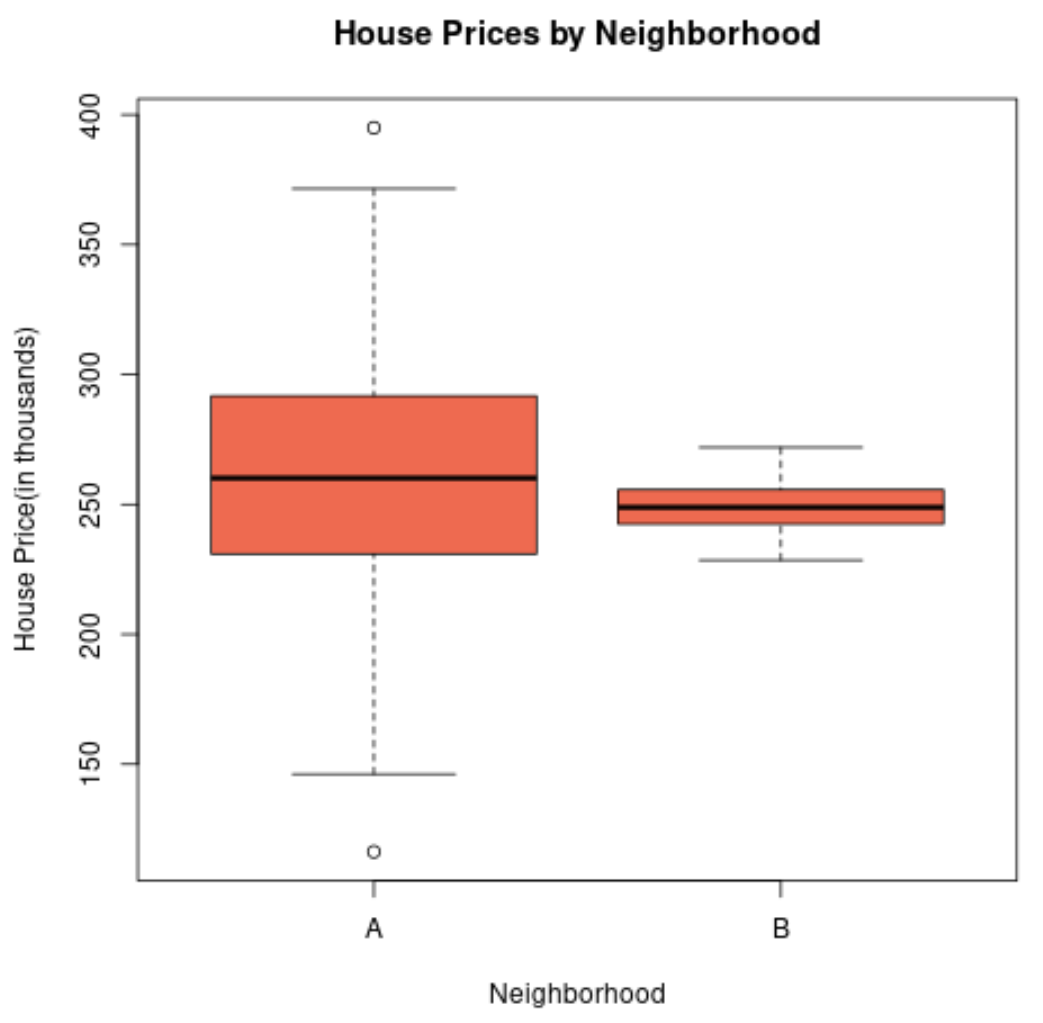
La longueur du boxplot du quartier A est d’autant plus grande que l’écart type des prix de l’immobilier est bien plus élevé.

En fait, les prix des logements varient de moins de 150 000 $ à plus de 400 000 $ pour le quartier A, tandis que les prix ne varient que d’environ 230 000 $ à 270 000 $ pour le quartier B.

En connaissant simplement l’écart type des prix de l’immobilier dans chaque quartier, nous pouvons savoir à quelle variation s’attendre dans les prix dans chaque quartier.

Ressources additionnelles

Qu’est-ce qui est considéré comme un bon écart type ?
Plage par rapport à l’écart type : quand utiliser chacun
Coefficient de variation par rapport à l’écart type : la différence