Qu’est-ce que la précision équilibrée ? (Définition & #038; Exemple)

La précision équilibrée est une mesure que nous pouvons utiliser pour évaluer les performances d’un modèle de classification .

Il est calculé comme suit :

Précision équilibrée = (Sensibilité + Spécificité) / 2

où:

• Sensibilité : Le « vrai taux de positif » – le pourcentage de cas positifs que le modèle est capable de détecter.
• Spécificité : Le « vrai taux négatif » – le pourcentage de cas négatifs que le modèle est capable de détecter.

Cette métrique est particulièrement utile lorsque les deux classes sont déséquilibrées, c’est-à-dire qu’une classe apparaît beaucoup plus que l’autre.

L’exemple suivant montre comment calculer la précision équilibrée dans la pratique et démontre pourquoi il s’agit d’une mesure si utile.

Exemple : calcul de la précision équilibrée

Supposons qu’un analyste sportif utilise un modèle de régression logistique pour prédire si 400 joueurs de basket-ball universitaires différents seront recrutés ou non dans la NBA.

La matrice de confusion suivante résume les prédictions faites par le modèle :

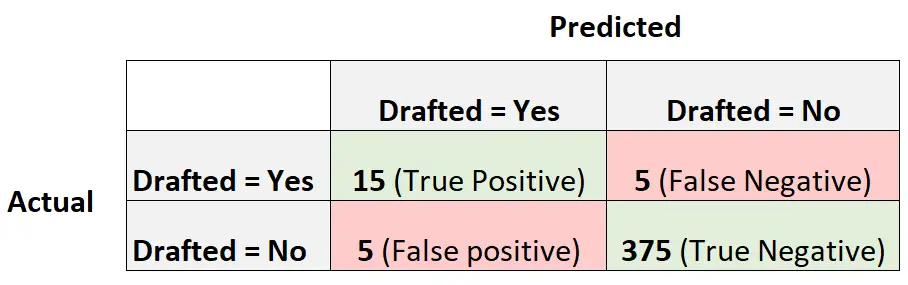
Pour calculer la précision équilibrée du modèle, nous allons d’abord calculer la sensibilité et la spécificité :

• Sensibilité : Le « taux de vrais positifs » = 15 / (15 + 5) = 0,75
• Spécificité : Le « taux vrai négatif » = 375 / (375 + 5) = 0,9868

Nous pouvons alors calculer la précision équilibrée comme suit :

• Précision équilibrée = (Sensibilité + Spécificité) / 2
• Précision équilibrée = (0,75 + 9868) / 2
• Précision équilibrée = 0,8684

La précision équilibrée du modèle s’avère être de 0,8684 .

Notez que plus la précision équilibrée est proche de 1, plus le modèle est capable de classer correctement les observations.

Dans cet exemple, la précision équilibrée est assez élevée, ce qui nous indique que le modèle de régression logistique fait un très bon travail pour prédire si les joueurs universitaires seront ou non recrutés dans la NBA.

Dans ce scénario, étant donné que les classes sont très déséquilibrées (20 joueurs ont été repêchés et 380 joueurs non), la précision équilibrée nous donne une image plus réaliste des performances du modèle par rapport à une mesure de précision globale.

Par exemple, nous calculerions la précision du modèle comme suit :

• Précision = (TP + TN) / (TP + TN + FP + FN)
• Précision = (15 + 375) / (15 + 375 + 5 + 5)
• Précision = 0,975

La précision du modèle est de 0,975 , ce qui semble extrêmement élevé.

Cependant, considérons un modèle qui prédit simplement que chaque joueur ne sera pas repêché. Il aurait une précision de 380/400 = 0,95 . Ce n’est que légèrement inférieur à la précision de notre modèle.

Le score de précision équilibré de 0,8684 nous donne une meilleure idée de la capacité du modèle à prédire les deux classes.

Autrement dit, cela nous donne une meilleure idée de la capacité du modèle à prédire les joueurs qui ne seront pas repêchés et ceux qui le seront.

Ressources additionnelles

Les tutoriels suivants expliquent comment créer une matrice de confusion dans différents logiciels statistiques :

Comment créer une matrice de confusion dans Excel
Comment créer une matrice de confusion dans R
Comment créer une matrice de confusion en Python