Probabilité conditionnelle (ou probabilité conditionnelle)

Vous découvrirez ici ce qu’est la probabilité conditionnelle (ou probabilité conditionnelle). Nous expliquons comment la probabilité conditionnelle est calculée avec un exemple et les propriétés de ce type de probabilité. De plus, vous pourrez vous entraîner avec des exercices résolus étape par étape de probabilité conditionnelle.

Qu’est-ce que la probabilité conditionnelle ?

La probabilité conditionnelle , également appelée probabilité conditionnelle , est une mesure statistique qui indique la probabilité qu’un événement A se produise si un autre événement B se produit. Autrement dit, la probabilité conditionnelle P(A|B) fait référence à la probabilité qu’un événement A se produise une fois que l’événement B s’est déjà produit.

La probabilité conditionnelle s’écrit avec une barre verticale entre les deux événements : P(A|B), et se lit comme suit : « la probabilité conditionnelle de l’événement A étant donné l’événement B ».

Notez que la valeur de la probabilité conditionnelle est un nombre compris entre 0 et 1. Plus la probabilité conditionnelle est élevée, plus il est probable que l’événement A se produise lorsque l’événement B se produit, mais plus la probabilité conditionnelle est faible, moins il est probable que l’événement A se produira lorsque l’événement B se produira.

Formule de probabilité conditionnelle

La probabilité conditionnelle de l’événement A étant donné l’événement B est égale à la probabilité de l’intersection entre l’événement A et l’événement B divisée par la probabilité de l’événement B.

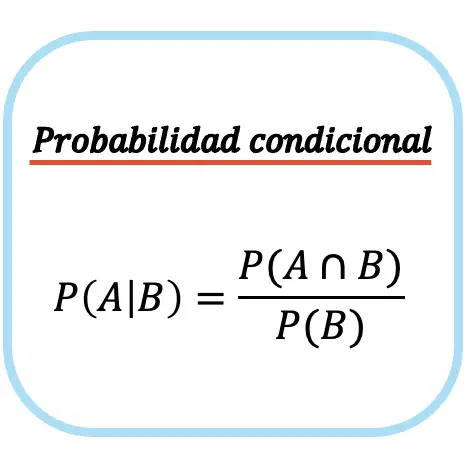
Notez que la formule de probabilité conditionnelle (ou probabilité conditionnelle) ne peut être utilisée que si la probabilité d’occurrence de l’événement inconditionné est différente de zéro, c’est-à-dire P(B)≠0. Ou autrement dit, s’il est possible que l’événement B se produise.

La probabilité conditionnelle peut également être calculée à partir de son inverse, c’est-à-dire que si P(B|A) est connu, P(A|B) peut être déterminé. Mais pour ce faire vous devez appliquer le théorème de Bayes, vous pouvez voir en quoi consiste ce théorème ici :

Exemple de probabilité conditionnelle

Une fois que nous avons vu quelle est la définition et la formule de la probabilité conditionnelle, nous allons résoudre étape par étape un exemple de ce type de probabilité pour bien comprendre sa signification.

• Après avoir passé un examen dans une classe de 30 étudiants, des données ont été collectées pour savoir combien d’étudiants ont étudié et combien ont réussi. Les résultats sont présentés dans le tableau de contingence suivant. À partir des données collectées, calculez la probabilité conditionnelle de réussir un examen si vous avez déjà étudié.

Pour obtenir la probabilité conditionnelle, nous devons appliquer la formule que nous avons vue précédemment :

Par conséquent, nous devons d’abord trouver la probabilité qu’un étudiant ait étudié et qu’il ait étudié et réussi. Pour trouver la probabilité qu’un étudiant ait étudié, nous devons simplement utiliser la règle de Laplace, c’est-à-dire que nous divisons le nombre d’étudiants qui ont étudié par le nombre total d’observations :

Et nous pouvons connaître la probabilité qu’un étudiant ait étudié et réussi en même temps à partir du tableau de contingence en divisant le nombre d’étudiants qui ont étudié et réussi par le total :

Ainsi, la probabilité qu’un étudiant réussisse un examen s’il a étudié est :

Probabilité conditionnelle d’événements dépendants et indépendants

Dans cette section, nous verrons quelle est la relation entre la probabilité conditionnelle et les événements dépendants et indépendants (ou les événements dépendants et indépendants). Car, bien qu’il s’agisse de concepts différents, ces deux types d’événements sont liés à une probabilité conditionnelle.

Deux événements (ou occurrences) sont indépendants lorsque leur probabilité d’occurrence ne dépend pas l’une de l’autre. Dans un tel cas, l’intersection entre les deux événements équivaut au produit de la probabilité de chaque événement séparément. Et, par conséquent, la formule de probabilité conditionnelle est simplifiée :

En bref, si les événements A et B sont indépendants, la probabilité conditionnelle de l’événement A étant donné l’événement B est exactement égale à la probabilité d’occurrence de l’événement A.

En revanche, lorsque deux événements sont dépendants, cela signifie que la probabilité d’un événement dépend de la probabilité de l’autre événement. Par conséquent, lorsque deux événements A et B sont dépendants, la probabilité conditionnelle de l’événement A étant donné l’événement B est différente de la probabilité d’occurrence de l’événement A.

Exercices résolus de probabilité conditionnelle

Exercice 1

On sait que dans un sac rempli de balles, la moitié est orange et l’autre moitié est verte. De plus, un tiers de toutes les balles sont orange et en même temps marquées d’un panneau. Quelle est la probabilité que lorsque vous tirez une boule orange, elle reçoive le signal ?

Pour résoudre l’exercice, nous devons appliquer la formule de probabilité conditionnelle, qui est :

L’énoncé du problème nous dit que la moitié du sac est constituée d’oranges. Par conséquent, la probabilité théorique de ramasser une balle orange est de 50 %.

Par contre, on sait qu’un tiers du total sont des boules orange et ont un signal, donc la probabilité d’obtenir une boule orange avec un signal est :

Enfin, nous substituons les probabilités calculées dans la formule de probabilité conditionnelle pour trouver sa valeur :

En résumé, la probabilité de tirer une boule avec le signal si elle est orange est de 66 %.

Exercice 2

Si nous avons six stylos bleus et trois stylos noirs dans une boîte, calculez la probabilité de tirer un seul stylo bleu et la probabilité de tirer deux stylos bleus consécutivement.

Pour déterminer la probabilité de ramasser un stylo bleu une fois, utilisez simplement la loi de Laplace :

Le problème nous demande également de connaître la probabilité de ramasser deux stylos bleus consécutivement, c’est-à-dire la probabilité conditionnelle de ramasser un stylo bleu si nous avons déjà ramassé un stylo bleu auparavant.

Si nous dessinons un stylo bleu, nous avons un cas moins favorable, mais il y a aussi un stylo de moins dans le total. La probabilité conditionnelle est donc :

Exercice 3

Quelle est la probabilité conditionnelle d’obtenir le chiffre 4 en lançant un dé étant donné qu’un tirage au sort donne face ?

Pour résoudre cet exercice, vous devez prendre en compte la théorie des probabilités conditionnelles, car les événements « obtenir le chiffre 4 en lançant un dé » et « obtenir face en lançant une pièce de monnaie » sont indépendants. Il n’est donc pas nécessaire d’utiliser la formule de probabilité conditionnelle, mais l’égalité suivante est satisfaite :

Ainsi, pour trouver la probabilité conditionnelle, il suffit d’utiliser la règle de Laplace :

Exercice 4

L’exercice financier de 25 entreprises d’un pays a été étudié et comment le prix de leurs actions évolue en fonction du résultat économique de l’année. Vous pouvez voir les données collectées dans le tableau de contingence suivant :

Quelle est la probabilité que le cours de l’action d’une entreprise augmente si elle a réalisé des bénéfices au cours de l’année écoulée ?

L’exercice nous interroge sur la probabilité conditionnelle que les actions augmentent étant donné que l’entreprise a obtenu un résultat économique positif. Donc, pour calculer cette probabilité, il faut utiliser la formule de probabilité conditionnelle :

Nous calculons donc d’abord la probabilité qu’une entreprise réalise un profit et, d’autre part, la probabilité qu’une entreprise réalise un bénéfice économique tout en augmentant son prix par action :

Et puis nous substituons les valeurs trouvées dans la formule et calculons la probabilité conditionnelle :

Propriétés de probabilité conditionnelle

Les propriétés de la probabilité conditionnelle, ou probabilité conditionnelle, sont les suivantes :

• La somme de la probabilité conditionnelle de l’événement A un événement donné B plus la probabilité conditionnelle de l’événement complémentaire de A un événement donné B est égale à un.

• Si l’événement A est un sous-ensemble de l’événement B, A se produira toujours lorsque B est vrai. Ainsi, la probabilité conditionnelle de l’événement A étant donné l’événement B dans ces cas est de 1.

• Étant donné deux événements différents, l’égalité suivante en ce qui concerne la probabilité conditionnelle est toujours vraie :