Comment calculer la probabilité conditionnelle dans Excel

La probabilité conditionnelle que l’événement A se produise, étant donné que l’événement B s’est produit, est calculée comme suit :

P(UNE|B) = P(UNE∩B) / P(B)

où:

P(A∩B) = la probabilité que l’événement A et l’événement B se produisent tous deux.

P(B) = la probabilité que l’événement B se produise.

Cette formule est particulièrement utile lors du calcul des probabilités pour un tableau à double entrée, qui est un tableau qui affiche les fréquences (ou « comptes ») pour deux variables catégorielles.

Par exemple, le tableau à double entrée suivant présente les résultats d’une enquête qui a demandé à 300 personnes quel sport elles préféraient : le baseball, le basket-ball, le football ou le football. Les lignes affichent le sexe du répondant et les colonnes indiquent le sport qu’il a choisi :

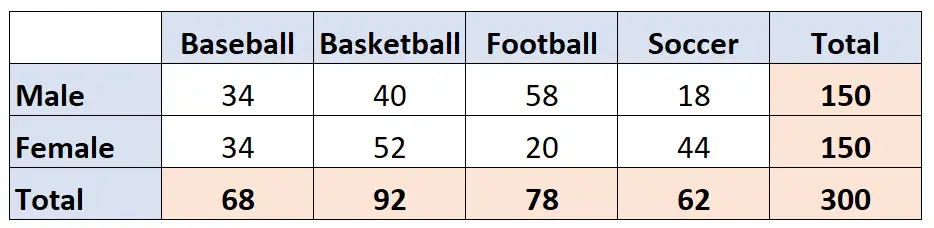
Il s’agit d’un tableau à double entrée car nous avons deux variables catégorielles : le sexe et le sport préféré.

Nous montrerons ensuite comment calculer les probabilités conditionnelles pour les tableaux bidirectionnels dans Excel.

Comment calculer la probabilité conditionnelle dans Excel

Supposons que nous souhaitions répondre à des questions telles que :

« Quelle est la probabilité qu’un répondant soit un homme, étant donné que son sport préféré est le baseball ? »

Nous pouvons trouver la réponse en utilisant la formule de probabilité conditionnelle :

P(mâle|baseball) = P(mâle∩baseball) / P(baseball) = (34/300) / (68/300) = 0,5

Ainsi, la probabilité qu’un répondant soit un homme, étant donné que son sport préféré est le baseball, est de 0,5 (soit 50 %).

Nous pouvons calculer les probabilités conditionnelles pour d’autres scénarios du tableau en utilisant une formule similaire. L’image ci-dessous montre comment calculer chaque probabilité conditionnelle du tableau, ainsi que la formule utilisée :

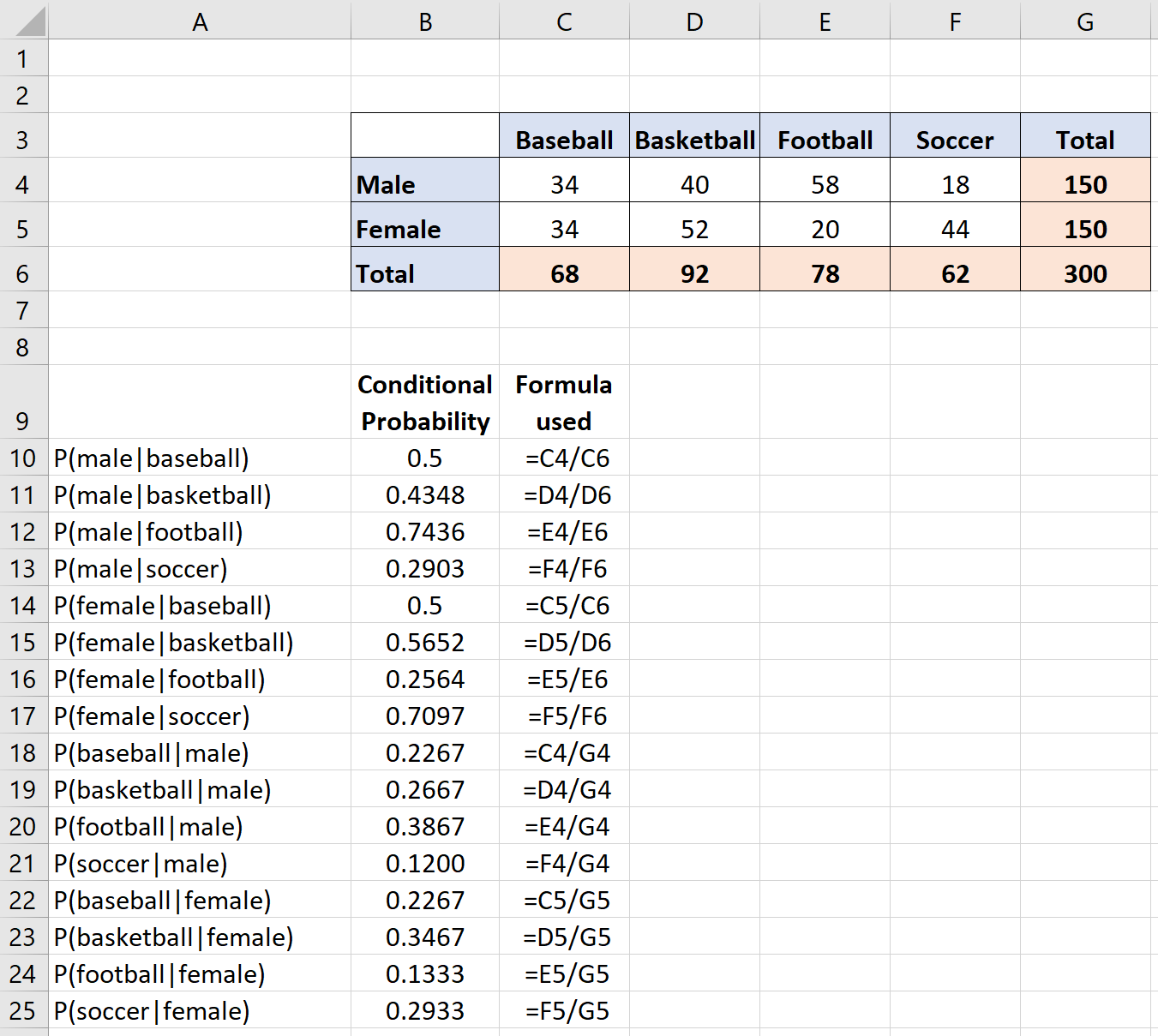
Notez que pour chaque calcul de probabilité conditionnelle, nous utilisons simplement la formule de probabilité conditionnelle de P(A|B) = P(A∩B) / P(B).

Par exemple, la probabilité que le sport préféré d’un répondant soit le football, étant donné qu’il s’agit d’une femme, est calculée comme suit :

P(football|femelle) = P(football∩femelle) / P(femelle)

Sur les 300 répondants, il y en a exactement 44 qui sont des femmes et préfèrent le football comme sport préféré, donc P(soccer∩femelle) = 44/300.

Et sur les 300 répondants, il y en a 150 qui sont des femmes, donc P(femelle) = 150/300.

Ainsi, P(soccer|female) = P(soccer∩female) / P(female) = (44/300) / (150/300) = 0,2933 .

Nous effectuons un calcul similaire pour chaque scénario de probabilité conditionnelle.

Ressources additionnelles

Comment trouver une fréquence relative conditionnelle dans un tableau à double entrée
Qu’est-ce qu’une distribution conditionnelle en statistiques ?