Probabilité d’intersection des événements

Cet article explique comment calculer la probabilité d’intersection des événements. Vous découvrirez donc quelle est la formule de la probabilité d’intersection des événements et, en plus, des exercices résolus étape par étape.

Quelle est l’intersection des événements ?

En théorie des probabilités, l’ intersection d’événements est une opération d’événements dont le résultat est composé des événements élémentaires communs à tous les événements de l’opération. Autrement dit, l’intersection des événements A et B est formée par tous les événements qui appartiennent à A et B en même temps.

L’intersection de deux événements est exprimée par le symbole ⋂. Ainsi, l’intersection des événements A et B s’écrit A⋂B.

Par exemple, dans l’expérience aléatoire consistant à lancer un dé, si un événement est qu’un nombre pair est lancé A={2, 4, 6} et qu’un autre événement est qu’un nombre supérieur à trois est lancé B={4, 5, 6 }, l’intersection des deux événements est A⋂B={4, 6}.

Formule pour la probabilité d’intersection des événements

La probabilité de l’intersection de deux événements est égale à la probabilité qu’un événement se produise multipliée par la probabilité conditionnelle que l’autre événement se produise étant donné le premier événement.

Par conséquent, la formule pour la probabilité de l’intersection de deux événements est P(A⋂B)=P(A) P(B|A)=P(B) P(A|B).

Où:

• et Ce sont deux événements dépendants.
• est la probabilité de l’intersection de l’événement A et de l’événement B.
• est la probabilité que l’événement A se produise.
• est la probabilité conditionnelle que l’événement B se produise étant donné l’événement A.
• est la probabilité que l’événement B se produise.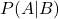
• est la probabilité conditionnelle que l’événement A se produise étant donné l’événement B.

Cependant, si les deux événements sont indépendants, cela signifie que la probabilité qu’un événement se produise ne dépend pas de la survenance ou non de l’autre événement. Par conséquent, la formule de la probabilité d’intersection des deux événements indépendants est la suivante :

Où:

• et Ce sont deux événements indépendants.
• est la probabilité de l’intersection de l’événement événement A et de l’événement B.
• est la probabilité que l’événement A se produise.
• est la probabilité que l’événement B se produise.

Exemples concrets de probabilité d’intersection d’événements

Ensuite, nous vous laissons deux exemples résolus étape par étape afin que vous puissiez voir comment est calculée la probabilité d’intersection de deux événements. Nous verrons d’abord un exemple d’intersection de deux événements indépendants puis de deux événements dépendants, afin que vous puissiez voir les deux cas.

Probabilité de l’intersection de deux événements indépendants

• Un tirage au sort est lancé trois fois de suite. Trouvez la probabilité d’obtenir face aux trois lancers.

Dans ce cas, les événements pour lesquels on veut calculer la probabilité conjointe sont indépendants, puisque le résultat d’un tirage au sort ne dépend pas du résultat obtenu lors du tirage au sort précédent. Par conséquent, pour déterminer la probabilité d’obtenir trois faces consécutives, nous devons utiliser la formule de probabilité d’intersection pour des événements indépendants :

Au tirage au sort, il n’y a que deux résultats possibles, nous pouvons obtenir pile ou face. Par conséquent, la probabilité d’obtenir pile ou face en lançant une pièce est :

Ainsi, pour trouver la probabilité d’obtenir face lors des trois lancers de pièces, nous devons multiplier par trois la probabilité d’obtenir face :

En bref, la probabilité d’obtenir face trois fois de suite est de 12,5 %.

Probabilité de l’intersection de deux événements dépendants

• Dans une boîte vide on met 8 boules bleues, 4 boules orange et 2 boules vertes. Si l’on tire d’abord une boule puis une autre boule sans remettre la première boule tirée dans la boîte, quelle est la probabilité que la première boule soit bleue et la deuxième boule orange ?

Dans ce cas, les événements sont dépendants, car la probabilité de ramasser une boule orange lors du deuxième tirage dépend de la couleur de la boule tirée lors du premier tirage. Par conséquent, pour calculer la probabilité que nous demande le problème, nous devons utiliser la formule de la probabilité d’intersection pour les événements dépendants :

La probabilité d’obtenir une boule bleue au premier tirage est facile à déterminer, il suffit de diviser le nombre de boules bleues par le nombre total de boules :

En revanche, la probabilité de tirer une boule orange après avoir pris une boule bleue est calculée différemment car le nombre de boules orange est différent et, en plus, il y a désormais une boule de moins à l’intérieur de la boîte :

Ainsi, la probabilité de tirer d’abord une boule bleue puis une boule orange se calcule en multipliant les deux probabilités trouvées ci-dessus :

Propriétés d’intersection d’événements

En théorie des probabilités, l’intersection des événements a les propriétés suivantes :

• Propriété commutative : l’ordre des événements d’intersection ne modifie pas le résultat de l’opération.

• Propriété associative : L’intersection de trois événements peut être calculée dans n’importe quel ordre, puisque le résultat est le même.

• Propriété distributive : l’intersection des événements satisfait la propriété distributive à l’union des événements.