Probabilité empirique

Dans cet article, nous expliquons comment calculer la probabilité empirique. Vous découvrirez ce qu’est la probabilité empirique, quelle est sa formule, un exemple et quelles sont les différences entre probabilité empirique et probabilité théorique.

Qu’est-ce que la probabilité empirique ?

La probabilité empirique est une mesure statistique basée sur des expériences ou des faits empiriques et qui indique la probabilité qu’un événement se produise.

Autrement dit, la probabilité empirique est calculée à partir des résultats d’une expérience et nous indique la probabilité qu’un événement se produise.

Plus l’expérience est répétée, plus la probabilité empirique obtenue sera précise. C’est pourquoi ce type de probabilité est généralement déterminé à l’aide de programmes informatiques qui simulent des milliers d’itérations et sont capables de les analyser en très peu de temps.

La probabilité empirique est un nombre compris entre 0 et 1. Plus un événement a de chances de se produire, plus la probabilité empirique est élevée, et inversement, moins un événement a de chances de se produire, plus sa probabilité empirique est faible.

Formule de probabilité empirique

La formule de probabilité empirique est le nombre de fois qu’un événement s’est produit au cours d’une expérience divisé par le nombre total de fois où l’expérience a été réalisée.

Par exemple, si nous regardons un arbre dix fois différentes et que nous avons vu à sept reprises un oiseau dans l’arbre, la probabilité empirique de voir un oiseau en regardant l’arbre sera :

Exemple de probabilité empirique

Compte tenu de la définition de la probabilité empirique, nous allons résoudre un exercice étape par étape sur ce type de probabilité. De cette façon, vous pouvez voir comment la probabilité empirique est calculée.

• Calcule la probabilité empirique des événements élémentaires qui composent l’expérience aléatoire consistant à lancer un dé.

Dans un premier temps, nous calculerons la probabilité théorique de comparer les résultats expérimentaux obtenus avec les résultats théoriques. Il y a six résultats possibles en lançant un dé (1, 2, 3, 4, 5 et 6), donc la probabilité théorique de chaque événement élémentaire est :

Pour résoudre cet exercice, nous devons simuler plusieurs fois le lancer d’un dé et noter les résultats dans un tableau de contingence. Pour cela, nous pouvons utiliser, par exemple, le programme Excel.

Pour que vous puissiez voir l’importance du nombre d’expériences réalisées, nous allons d’abord simuler dix lancements, puis une centaine et enfin mille. Ainsi, les résultats obtenus à partir de la simulation des 10 premiers lancers aléatoires d’un dé sont les suivants :

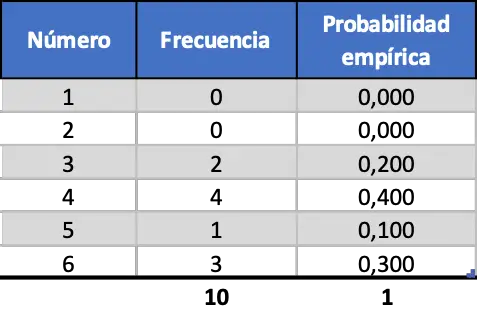
Comme vous pouvez le constater, les probabilités empiriques obtenues en simulant seulement dix lancers ne sont pas proches des probabilités théoriques (0,167).

Mais à mesure que nous augmentons le nombre d’expériences, ces deux mesures deviennent plus similaires, regardez la simulation de 100 lancements :

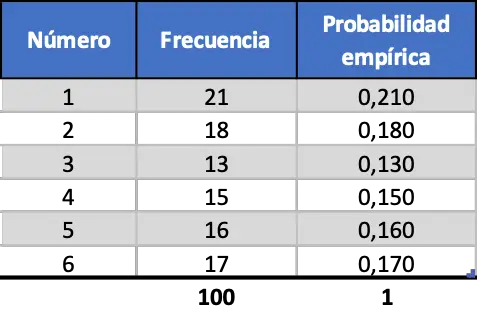
Maintenant, la probabilité empirique calculée pour chaque nombre sur le dé est plus similaire à la probabilité théorique, cependant, nous obtenons toujours des valeurs très différentes.

Finalement, on fait la même procédure mais en simulant 1000 lancements :

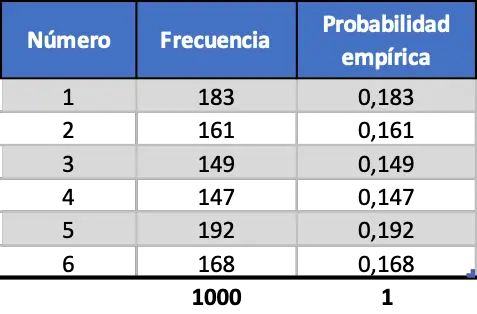
Comme on peut le voir dans le dernier tableau de contingence, désormais les valeurs des probabilités empiriques sont très proches des probabilités théoriques.

En résumé, plus on augmente le nombre d’expériences réalisées, plus la valeur de la probabilité empirique d’un événement sera proche de sa probabilité théorique d’occurrence . Cette règle est définie comme la loi des grands nombres , qui stipule que plus il y a de données, plus les valeurs expérimentales seront proches des valeurs théoriques.

De plus, si l’on compare les trois tableaux de fréquences, on constate que la probabilité empirique n’est pas définitive, mais qu’elle change en fonction du nombre d’expériences réalisées. Ce qui veut dire qu’il faut savoir interpréter les valeurs obtenues.

Probabilité empirique et probabilité théorique

Enfin, nous analyserons la notion de probabilité empirique et celle de probabilité théorique, car bien qu’il s’agisse de deux types de probabilités, elles ont une signification totalement différente.

La différence entre la probabilité empirique et la probabilité théorique (ou probabilité classique) réside dans le fait que la probabilité empirique est calculée à partir de données collectées à partir d’une expérience réelle, tandis que la probabilité théorique est calculée en tenant compte de circonstances idéales sans effectuer aucune expérience.

Autrement dit, pour trouver la probabilité empirique, une expérience doit être simulée et le calcul effectué sur la base des résultats obtenus. Mais pour connaître la probabilité théorique, aucune expérience ne doit être réalisée, mais plutôt un calcul théorique.

De plus, le niveau de biais est défini comme la différence entre la probabilité empirique et la probabilité théorique. Le biais peut être positif ou négatif, mais il est très difficile qu’il soit nul, car cela signifierait qu’une expérience aléatoire atteint juste la probabilité théorique, ce qui est très peu probable.