Probabilité expérimentale

Vous trouverez ici la signification de la probabilité expérimentale et comment la probabilité expérimentale est calculée. De plus, vous pourrez voir un exemple résolu étape par étape du calcul de la probabilité expérimentale.

Qu’est-ce que la probabilité expérimentale ?

La probabilité expérimentale est une mesure statistique basée sur les résultats d’une expérience ou des faits empiriques et indique la probabilité d’occurrence d’un événement.

De plus, plus l’expérience est répétée, plus la probabilité expérimentale obtenue sera précise. Pour cette raison, des programmes informatiques capables de simuler rapidement des milliers d’expériences sont généralement utilisés pour déterminer la probabilité expérimentale, obtenant ainsi une meilleure précision.

La probabilité expérimentale est également connue sous le nom de probabilité empirique ou probabilité de fréquence .

La probabilité expérimentale est un nombre compris entre 0 et 1. Logiquement, plus la valeur de la probabilité expérimentale d’un événement est grande, plus il est probable qu’il se produise, et vice versa, plus la valeur est petite, moins il est probable qu’il se produise. soit que l’événement se produise. Mais la valeur de la probabilité expérimentale sera toujours comprise entre zéro et un.

Formule de probabilité expérimentale

La formule de la probabilité expérimentale est le nombre de fois qu’un événement s’est produit au cours d’une expérience divisé par le nombre total de fois où l’expérience a été réalisée.

Par exemple, si une personne lance dix fléchettes sur une cible et parvient à toucher 6 fléchettes au centre, la probabilité que cette personne touche une fléchette au centre est calculée comme suit :

Exemple de probabilité expérimentale

Une fois que nous aurons vu la définition mathématique de la probabilité expérimentale, nous résoudrons ensuite un exercice étape par étape sur ce type de probabilité. L’objectif est que vous appreniez comment est calculée la probabilité expérimentale d’un événement, donc si vous avez des questions, vous pouvez les écrire dans les commentaires.

• Calculez la probabilité expérimentale des événements élémentaires qui composent l’expérience aléatoire consistant à lancer un dé.

Avant de trouver la probabilité expérimentale, nous calculerons la probabilité théorique pour comparer les résultats expérimentaux obtenus avec les résultats théoriques. Comme vous le savez bien, il y a six résultats possibles lorsqu’on lance un dé (1, 2, 3, 4, 5 et 6), donc la probabilité théorique de chaque événement élémentaire est :

Pour résoudre cet exercice, nous devons simuler plusieurs fois le lancer d’un dé et enregistrer les résultats dans un tableau de contingence. Dans ce cas, nous ferons les simulations avec le programme Excel, mais vous pouvez évidemment utiliser le programme de votre choix.

Nous simulerons d’abord dix lancers, puis cent lancers et enfin mille lancers. De cette façon, nous pourrons analyser les résultats et voir comment ils changent en fonction de la taille de l’échantillon de l’expérience. Les résultats obtenus après simulation aléatoire de 10 lancers de dés sont les suivants :

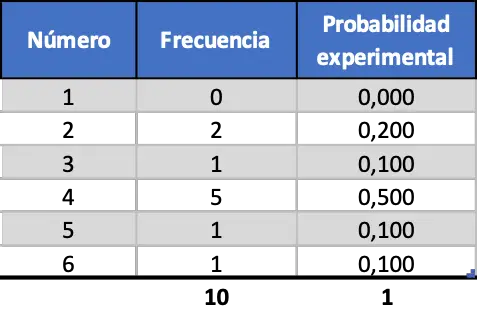
Comme vous pouvez le constater, les probabilités expérimentales obtenues sont actuellement assez différentes des probabilités théoriques calculées précédemment (0,167).

Mais à mesure que nous augmentons le nombre de tests, ces deux mesures deviennent plus similaires, jetez un œil à la simulation de 100 lancements :

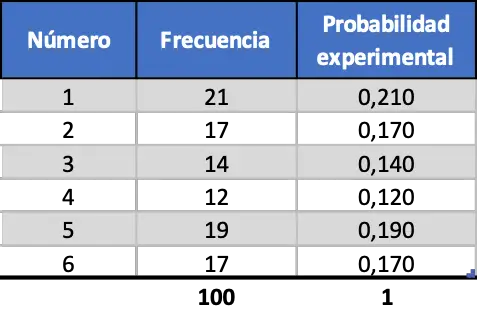
Maintenant, la probabilité expérimentale ressemble davantage à la valeur de la probabilité théorique, cependant, nous obtenons toujours des valeurs lointaines.

Finalement, on fait la même procédure mais en simulant 1000 lancements :

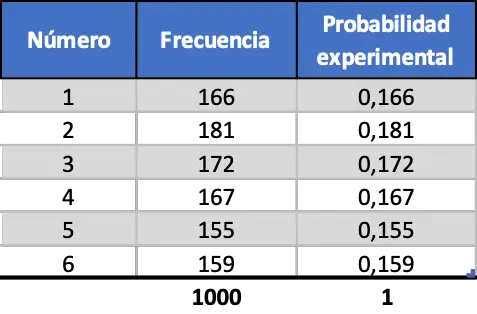
Comme vous pouvez le voir dans le dernier tableau de contingence, désormais les valeurs des probabilités expérimentales sont très similaires aux probabilités théoriques.

En résumé, plus le nombre d’expériences réalisées est grand, plus la valeur de la probabilité expérimentale d’un événement sera proche de sa probabilité théorique . Cette règle est définie comme la loi des grands nombres , qui stipule que plus il y a de données, plus les valeurs expérimentales seront proches des valeurs théoriques.

De même, si vous comparez les trois tableaux de fréquences, vous verrez que la probabilité expérimentale n’est pas définitive, mais qu’elle évolue en fonction du nombre d’expériences réalisées. Ce qui veut dire qu’il faut savoir interpréter les valeurs obtenues.

Probabilité expérimentale et probabilité théorique

La différence entre la probabilité expérimentale et la probabilité théorique (ou probabilité classique) réside dans le fait que la probabilité expérimentale est calculée à partir des données collectées à partir d’une expérience réelle, alors que la probabilité théorique est calculée sans qu’il soit nécessaire de réaliser aucune expérience.

Comme nous l’avons vu, nous devons simuler un grand nombre d’expériences pour en déduire la probabilité expérimentale d’un événement. Cependant, le calcul de la probabilité théorique repose sur la théorie et la logique. Vous pouvez voir comment cela se fait ici :