Probabilité postérieure : définition + exemple
Une probabilité a posteriori est la probabilité actualisée qu’un événement se produise après prise en compte de nouvelles informations.
Par exemple, nous pourrions être intéressés par la probabilité qu’un événement « A » se produise après avoir pris en compte un événement « B » qui vient de se produire. Nous pourrions calculer cette probabilité a posteriori en utilisant la formule suivante :
P(UNE|B) = P(UNE) * P(B|UNE) / P(B)
où:
P(A|B) = la probabilité que l’événement A se produise, étant donné que l’événement B s’est produit. Notez que « | » signifie « donné ».
P(A) = la probabilité que l’événement A se produise.
P(B) = la probabilité que l’événement B se produise.
P(B|A) = la probabilité que l’événement B se produise, étant donné que l’événement A s’est produit.
Exemple : Calcul de la probabilité postérieure
Une forêt est composée de 20% de chênes et de 80% d’érables. Supposons que l’on sache que 90 % des chênes sont en bonne santé alors que seulement 50 % des érables sont en bonne santé. Supposons que, de loin, vous puissiez dire qu’un arbre particulier est en bonne santé. Quelle est la probabilité que l’arbre soit un chêne ?
Rappelons que la probabilité que l’événement A se produise étant donné que l’événement B s’est produit est :
P(UNE|B) = P(UNE) * P(B|UNE) / P(B)
Dans cet exemple, la probabilité que l’arbre soit un chêne étant donné que l’arbre est en bonne santé est :
P(Chêne|Sain) = P(Chêne) * P(Sain|Chêne) / P(Sain)
P(Chêne) = La probabilité qu’un arbre donné soit un chêne est de 0,2 car 20 % de tous les arbres de la forêt sont des chênes.
P(Healthy) = La probabilité qu’un arbre donné soit en bonne santé peut être calculée comme suit : (0,20)*(0,9) + (0,8)*(0,5) = 0,58 .
P(Healthy|Oak) = La probabilité qu’un arbre soit en bonne santé étant donné qu’il s’agit d’un chêne est de 0,9 , puisqu’on nous a dit que 90 % des chênes sont en bonne santé.
En utilisant ces trois nombres, nous pouvons trouver la probabilité que l’arbre soit un chêne étant donné qu’il est en bonne santé :
P(Chêne|Sain) = P(Chêne) * P(Sain|Chêne) / P(Sain) = (0,2) * (0,9) / (0,58) = 0,3103 .
Pour une compréhension intuitive de cette probabilité, supposons que la grille suivante représente cette forêt de 100 arbres. Exactement 20 des arbres sont des chênes et 18 d’entre eux sont sains. Les 80 autres arbres sont des érables et 40 d’entre eux sont sains.
(O = Chêne, M = Érable, Vert = Sain, Rouge = Malsain)
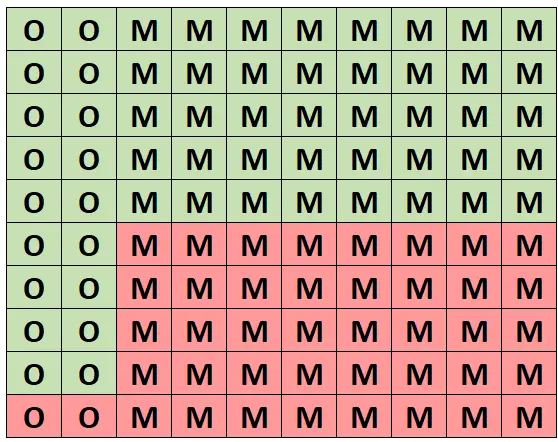
Sur tous les arbres, exactement 58 d’entre eux sont sains et 18 de ces arbres sains sont des chênes. Ainsi, si nous savons que nous avons sélectionné un arbre sain alors la probabilité qu’il s’agisse d’un chêne est de 18/58 = 0,3103 .
Quand devriez-vous utiliser la probabilité a posteriori ?
La probabilité a posteriori est utilisée dans une grande variété de domaines, notamment la finance, la médecine, l’économie et les prévisions météorologiques.
L’intérêt de l’utilisation des probabilités a posteriori est de mettre à jour une croyance antérieure que nous avions à propos de quelque chose une fois que nous obtenons de nouvelles informations.
Rappelons dans l’exemple précédent que nous savions que la probabilité qu’un arbre donné dans la forêt soit du chêne était de 20 %. C’est ce qu’on appelle une probabilité préalable . Si nous choisissions simplement un arbre au hasard, nous savions que la probabilité qu’il s’agisse d’un chêne était de 0,20.
Cependant, une fois que nous avons obtenu les nouvelles informations selon lesquelles l’arbre que nous avons sélectionné était en bonne santé, nous avons pu utiliser ces nouvelles informations pour déterminer que la probabilité a posteriori que cet arbre soit un chêne était plutôt de 0,3103.
Dans le monde réel, les gens découvrent constamment de nouvelles informations. Ces nouvelles informations nous aident à mettre à jour nos croyances antérieures. En termes statistiques, cela signifie que nous sommes capables de générer des probabilités a posteriori d’événements qui se produisent, ce qui nous aide à acquérir une compréhension plus précise du monde et nous permet de faire des prédictions plus précises sur les événements futurs.
