Comment calculer les probabilités normales sur une calculatrice TI-84

La distribution normale est la distribution la plus couramment utilisée dans toutes les statistiques. Ce didacticiel explique comment utiliser les fonctions suivantes sur une calculatrice TI-84 pour trouver les probabilités de distribution normale :

normalpdf(x, μ, σ) renvoie la probabilité associée à la pdf normale où :

• x = valeur individuelle
• μ = moyenne de la population
• σ = écart type de la population

normalcdf(lower_x, upper_x, μ, σ) renvoie la probabilité cumulée associée au cdf normal entre deux valeurs.

où:

• lower_x = valeur individuelle inférieure
• upper_x = valeur individuelle supérieure
• μ = moyenne de la population
• σ = écart type de la population

Ces deux fonctions sont accessibles sur une calculatrice TI-84 en appuyant sur 2nd puis en appuyant sur vars . Cela vous amènera à un écran DISTR où vous pourrez ensuite utiliser normalpdf() et normalcdf() :

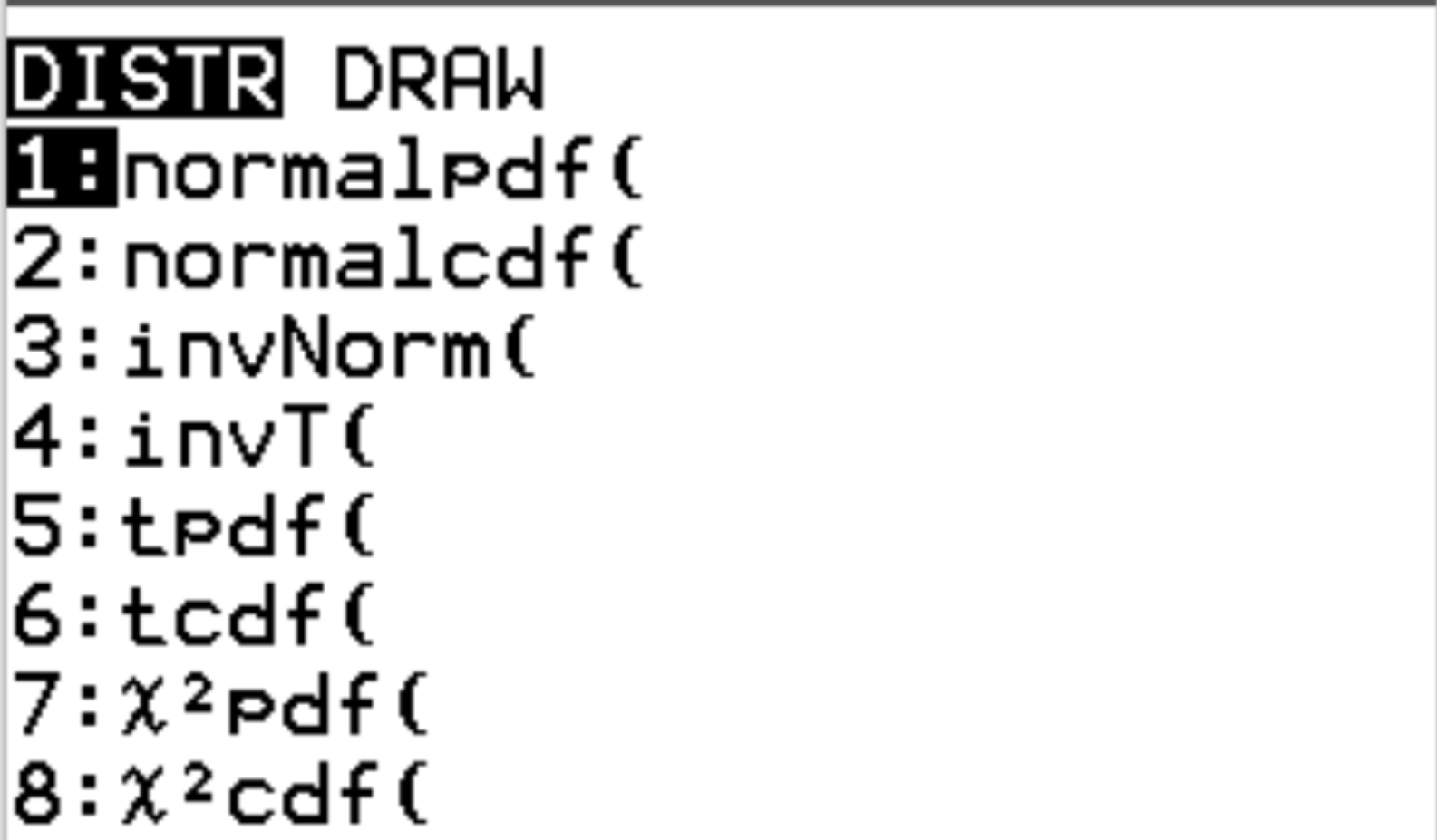
Les exemples suivants illustrent comment utiliser ces fonctions pour répondre à différentes questions.

Exemple 1 : probabilité normale supérieure à x

Question : Pour une distribution normale avec moyenne = 40 et écart type = 6, trouvez la probabilité qu’une valeur soit supérieure à 45.

Réponse : Utilisez la fonction normalcdf(x, 10000, μ, σ) :

normalcdf(45, 10000, 40, 6) = 0,2023

Remarque : Puisque la fonction nécessite une valeur upper_x, nous utilisons simplement 10 000.

Exemple 2 : probabilité normale inférieure à x

Question : Pour une distribution normale avec moyenne = 100 et écart type = 11,3, trouvez la probabilité qu’une valeur soit inférieure à 98.

Réponse : Utilisez la fonction normalcdf(-10000, x, μ, σ) :

normalcdf(-10000, 98, 100, 11,3) = 0,4298

Remarque : Puisque la fonction nécessite une valeur lower_x, nous utilisons simplement -10000.

Exemple 3 : Probabilité normale entre deux valeurs

Question : Pour une distribution normale avec moyenne = 50 et écart type = 4, trouvez la probabilité qu’une valeur soit comprise entre 48 et 52.

Réponse : Utilisez la fonction normalcdf(smaller_x, Larger_x, μ, σ)

normalcdf(48, 52, 50, 4) = 0,3829

Exemple 4 : Probabilité normale en dehors de deux valeurs

Question : Pour une distribution normale avec moyenne = 22 et écart type = 4, trouvez la probabilité qu’une valeur soit inférieure à 20 ou supérieure à 24.

Réponse : Utilisez la fonction normalcdf(-10000, small_x, μ, σ) + normalcdf(larger_x, 10000, μ, σ)

normalcdf(-10000, 20, 22, 4) + normalcdf(24, 10000, 22, 4) = 0,6171