Comment calculer un produit scalaire sur une calculatrice TI-84
Étant donné le vecteur a = [a 1 , a 2 , a 3 ] et le vecteur b = [b 1 , b 2 , b 3 ], le produit scalaire du vecteur a et du vecteur b, noté a · b , est donné par :
une · b = une 1 * b 1 + une 2 * b 2 + une 3 * b 3
Par exemple, si a = [2, 5, 6] et b = [4, 3, 2], alors le produit scalaire de a et b serait égal à :
une · b = 2*4 + 5*3 + 6*2
une · b = 8 + 15 + 12
une · b = 35
Nous pouvons utiliser la syntaxe suivante pour calculer le produit scalaire de deux vecteurs sur une calculatrice TI-84 :
sum({2, 5, 6}*{4, 3, 2})
L’exemple suivant étape par étape montre comment utiliser cette syntaxe dans la pratique.
Exemple : Calculer le produit scalaire sur la calculatrice TI-84
Suivez les étapes suivantes pour calculer le produit scalaire entre deux vecteurs :
Étape 1 : Entrez la commande sum(.
Tout d’abord, appuyez sur 2ème puis appuyez sur STAT puis faites défiler jusqu’à MATH et appuyez sur sum :
Étape 2 : Entrez l’accolade gauche.
Ensuite, appuyez sur 2ème puis appuyez sur ( pour saisir la première accolade :
Étape 3 : Saisissez les données
Ensuite, entrez les valeurs suivantes pour chaque vecteur :
- Vecteur a : 2, 5, 6
- Vecteur b : 4, 3, 2
Assurez-vous d’inclure un signe de multiplication entre les deux vecteurs et fermez la fin de la commande sum() avec une parenthèse à droite. Appuyez ensuite sur ENTER :
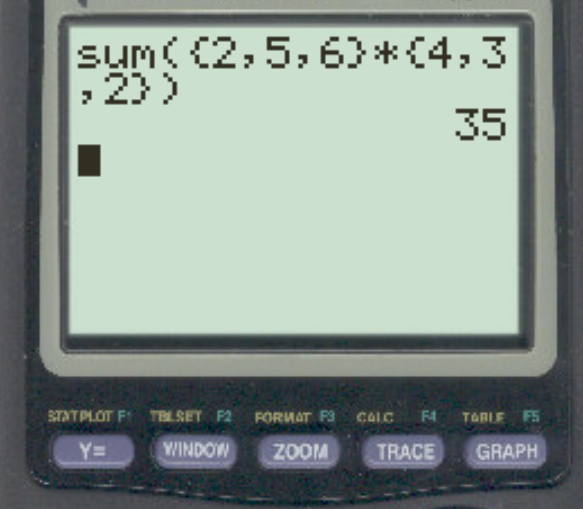
Le produit scalaire s’avère être 35 . Cela correspond à la valeur que nous avons calculée manuellement.
Ressources additionnelles
Comment calculer le produit scalaire dans Excel
Comment calculer le produit scalaire dans Google Sheets
Comment calculer le produit scalaire dans R
à propos de l'auteur
Dr. Benjamin Anderson
Il est un professeur de statistiques à la retraite devenu éducateur dévoué sur Statorials. Avec une vaste expérience et une expertise dans le domaine des statistiques, je m'engage à partager mes connaissances pour responsabiliser les étudiants grâce à Statorials. Lire plus