Quand devriez-vous utiliser la régression polynomiale ?

La régression polynomiale est une technique que nous pouvons utiliser pour ajuster un modèle de régression lorsque la relation entre la ou les variables prédictives et la variable de réponse est non linéaire.

Un modèle de régression polynomiale prend la forme suivante :

Y = β ₀ + β ₁ X + β ₂ X ² + … + β _h X ^h + ε

En pratique, il existe trois façons simples de déterminer si vous devez utiliser la régression polynomiale par rapport à un modèle plus simple comme la régression linéaire .

1. Créez un nuage de points de la variable prédictive et de la variable de réponse

Le moyen le plus simple de déterminer si vous devez utiliser la régression polynomiale consiste à créer un simple nuage de points de la variable prédictive et de la variable de réponse.

Par exemple, supposons que nous souhaitions utiliser la variable prédictive « heures d’études » pour prédire la note qu’un étudiant obtiendra à un examen final.

Avant d’ajuster un modèle de régression, nous pouvons d’abord créer un nuage de points des heures étudiées par rapport aux résultats de l’examen. Supposons que notre nuage de points ressemble à ceci :

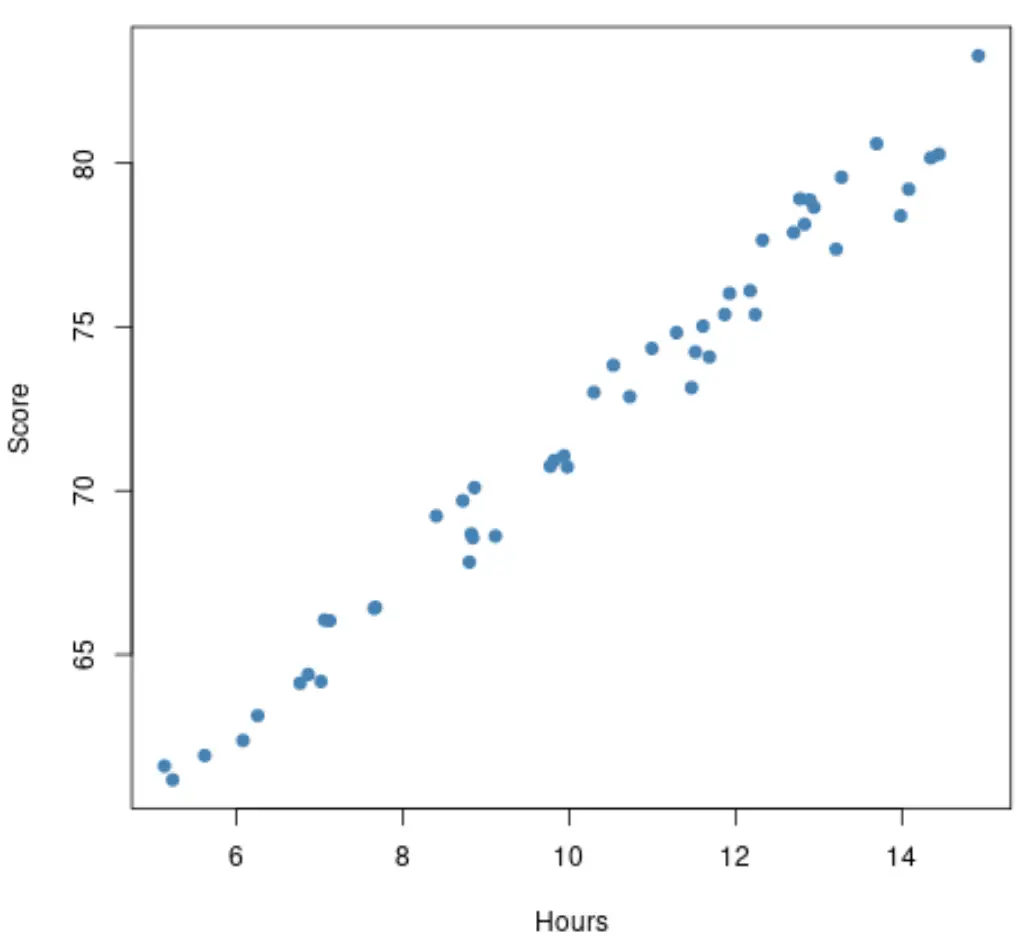
La relation entre les heures étudiées et les résultats de l’examen semble linéaire , il serait donc logique d’adapter un modèle de régression linéaire simple à cet ensemble de données.

Cependant, supposons que le nuage de points ressemble réellement à ce qui suit :

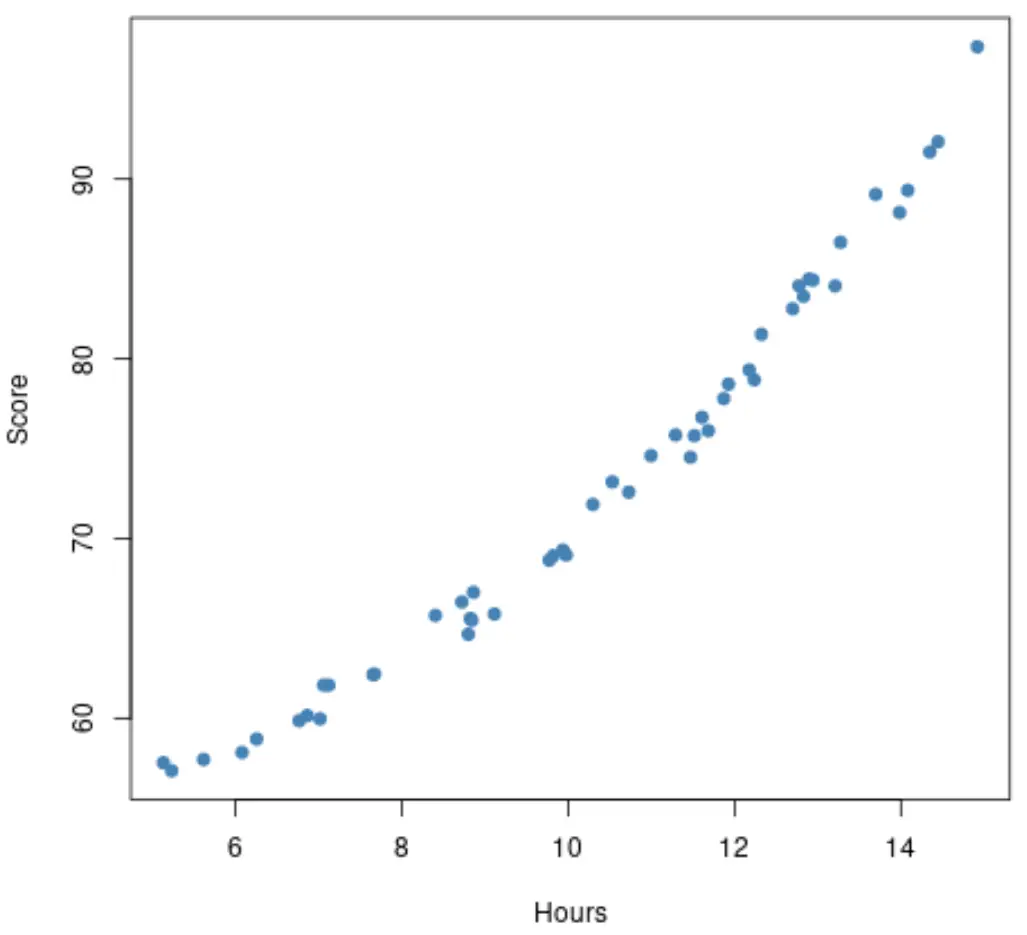
Cette relation semble un peu plus non linéaire , ce qui nous indique qu’il peut être judicieux d’adapter plutôt un modèle de régression polynomiale.

2. Créer un graphique de valeurs ajustées et résiduelles

Une autre façon de déterminer si vous devez utiliser la régression polynomiale consiste à ajuster un modèle de régression linéaire à l’ensemble de données, puis à créer un tracé des valeurs ajustées par rapport aux résidus pour le modèle.

S’il existe une tendance non linéaire claire dans les résidus, cela indique que la régression polynomiale pourrait offrir un meilleur ajustement aux données.

Par exemple, supposons que nous ajustions un modèle de régression linéaire en utilisant les heures étudiées comme variable prédictive et le score d’examen comme variable de réponse, puis créons le graphique des valeurs ajustées par rapport aux résidus suivant :

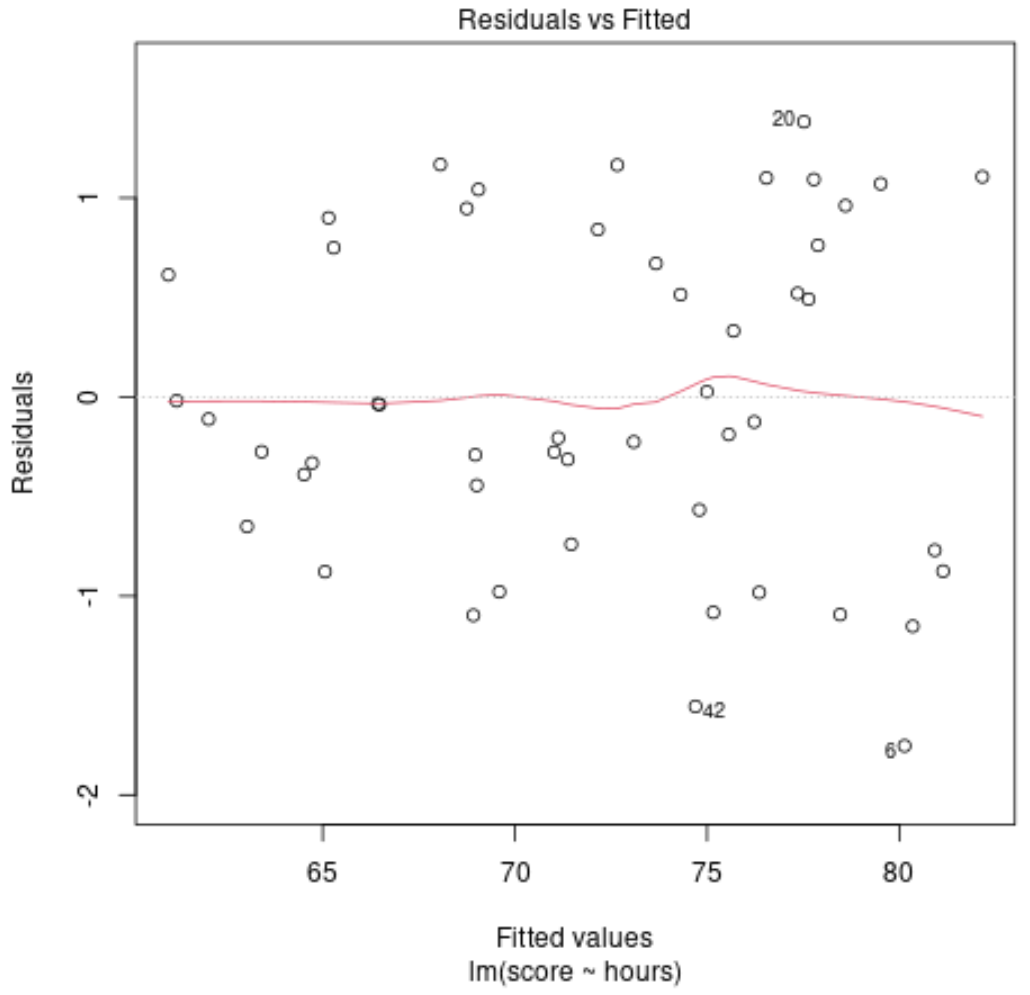
Les résidus sont dispersés de manière aléatoire autour de zéro sans motif clair, ce qui indique qu’un modèle linéaire fournit un ajustement approprié aux données.

Cependant, supposons que notre graphique des valeurs ajustées par rapport aux résidus ressemble réellement à ce qui suit :

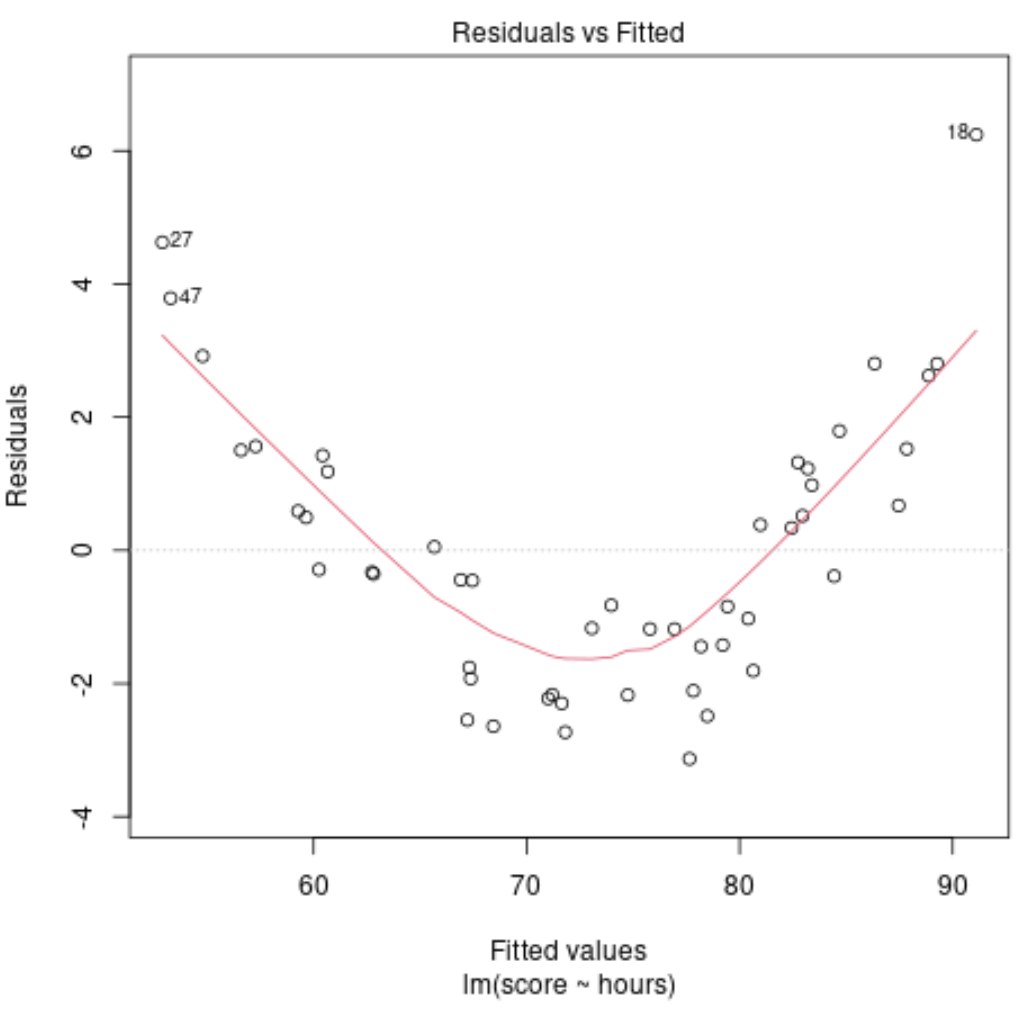
Sur le graphique, nous pouvons voir qu’il existe un motif non linéaire clair dans les résidus – les résidus présentent une forme en « U ».

Cela nous indique qu’un modèle linéaire n’est pas approprié pour ces données particulières et qu’il pourrait être judicieux d’ajuster plutôt un modèle de régression polynomiale.

3. Calculer la valeur R-carré ajustée du modèle

Une autre façon de déterminer si vous devez utiliser la régression polynomiale consiste à ajuster à la fois un modèle de régression linéaire et un modèle de régression polynomiale et à calculer les valeurs R au carré ajustées pour les deux modèles.

Le R au carré ajusté représente la proportion de la variance de la variable de réponse qui peut être expliquée par les variables prédictives du modèle, ajustée en fonction du nombre de variables prédictives du modèle.

Le modèle avec le R carré ajusté le plus élevé représente le modèle qui est le mieux à même d’utiliser la ou les variables prédictives pour expliquer la variation de la variable de réponse.

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer une régression polynomiale à l’aide de différents logiciels statistiques :

Une introduction à la régression polynomiale
Comment effectuer une régression polynomiale dans R
Comment effectuer une régression polynomiale en Python
Comment effectuer une régression polynomiale dans Excel