Comment calculer l’erreur quadratique moyenne (RMSE) dans Excel

En statistique, l’analyse de régression est une technique que nous utilisons pour comprendre la relation entre une variable prédictive, x, et une variable de réponse, y.

Lorsque nous effectuons une analyse de régression, nous obtenons un modèle qui nous indique la valeur prédite de la variable de réponse en fonction de la valeur de la variable prédictive.

Une façon d’évaluer dans quelle mesure notre modèle s’adapte à un ensemble de données donné consiste à calculer l’ erreur quadratique moyenne , qui est une métrique qui nous indique à quel point nos valeurs prédites sont éloignées de nos valeurs observées, en moyenne.

La formule pour trouver l’erreur quadratique moyenne, plus communément appelée RMSE , est la suivante :

RMSE = √[ Σ(P _i – O _i ) ² / n ]

où:

• Σ est un symbole fantaisiste qui signifie « somme »
• P _i est la valeur prédite pour la ^ième observation dans l’ensemble de données
• O _i est la valeur observée pour la ^ième observation dans l’ensemble de données
• n est la taille de l’échantillon

Notes techniques :

• L’erreur quadratique moyenne peut être calculée pour tout type de modèle produisant des valeurs prédites, qui peuvent ensuite être comparées aux valeurs observées d’un ensemble de données.
• L’erreur quadratique moyenne est aussi parfois appelée écart quadratique moyen, qui est souvent abrégé en RMSD.

Examinons ensuite un exemple de la façon de calculer l’erreur quadratique moyenne dans Excel.

Comment calculer l’erreur quadratique moyenne dans Excel

Il n’existe pas de fonction intégrée pour calculer le RMSE dans Excel, mais nous pouvons le calculer assez facilement avec une seule formule. Nous montrerons comment calculer le RMSE pour deux scénarios différents.

Scénario 1

Dans un scénario, vous pouvez avoir une colonne contenant les valeurs prédites de votre modèle et une autre colonne contenant les valeurs observées. L’image ci-dessous montre un exemple de ce scénario :

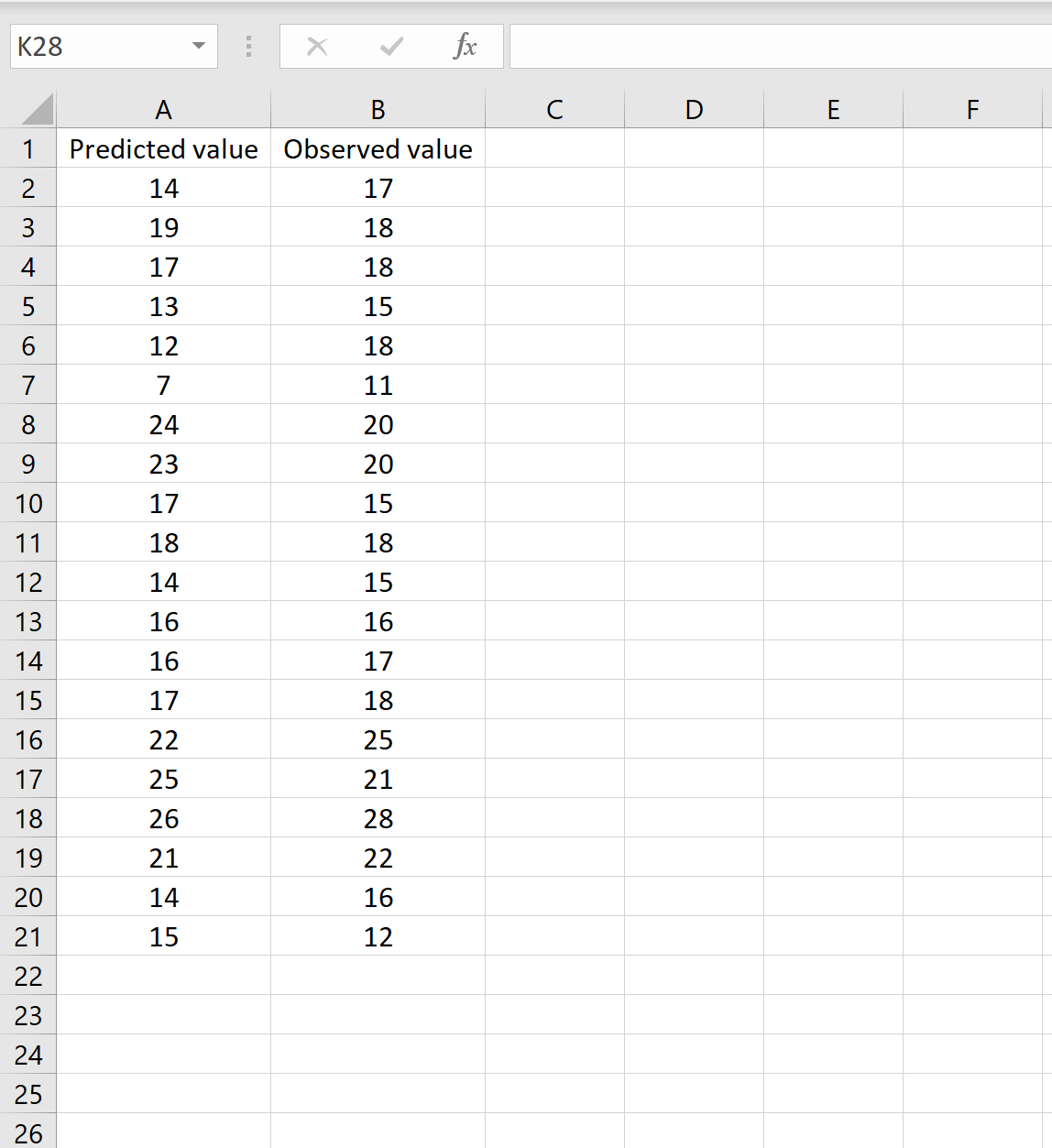
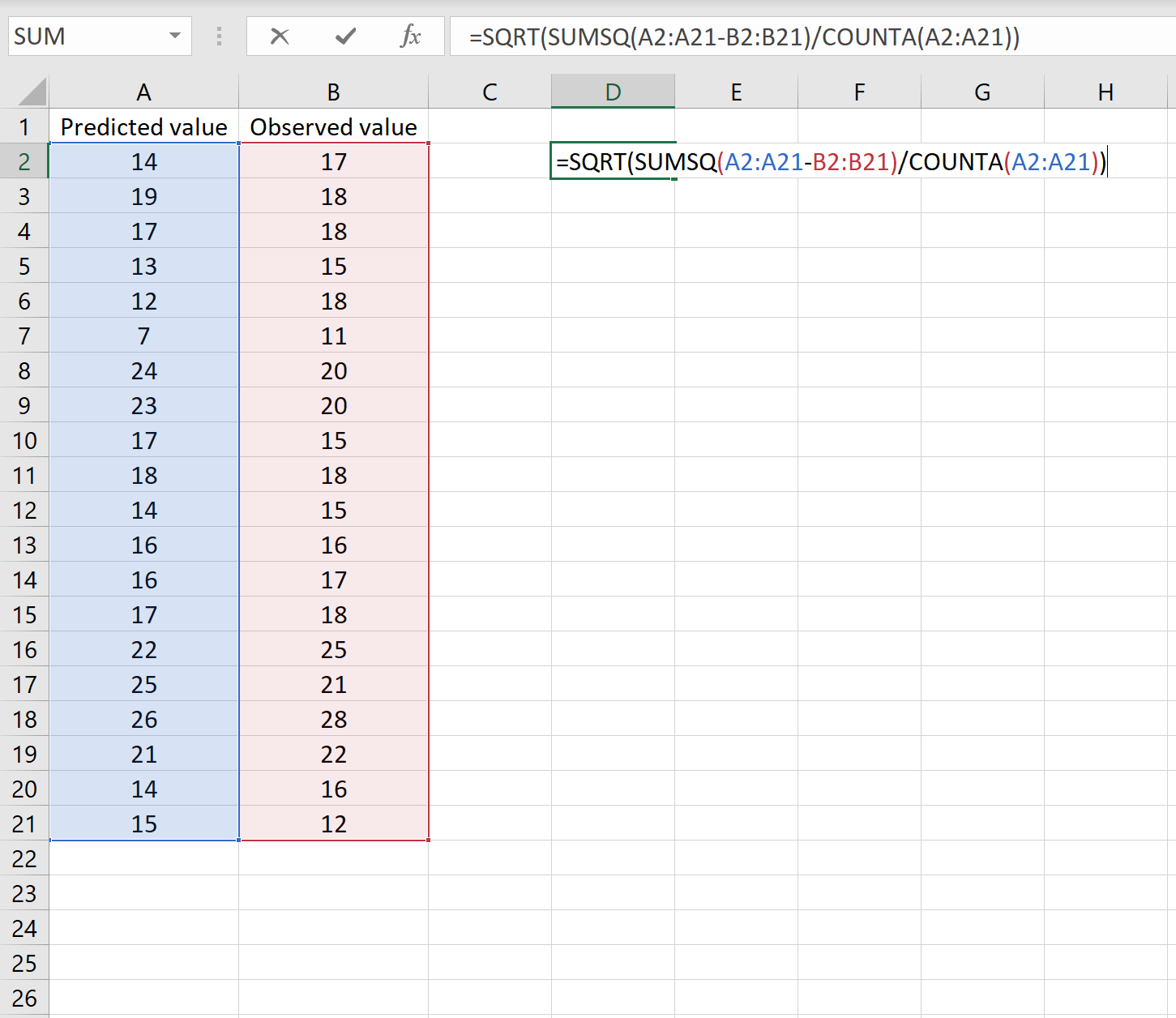
Si tel est le cas, vous pouvez calculer le RMSE en tapant la formule suivante dans n’importe quelle cellule, puis en cliquant sur CTRL+MAJ+ENTRÉE :

=SQRT(SUMSQ(A2:A21-B2:B21) / COMPTE(A2:A21))

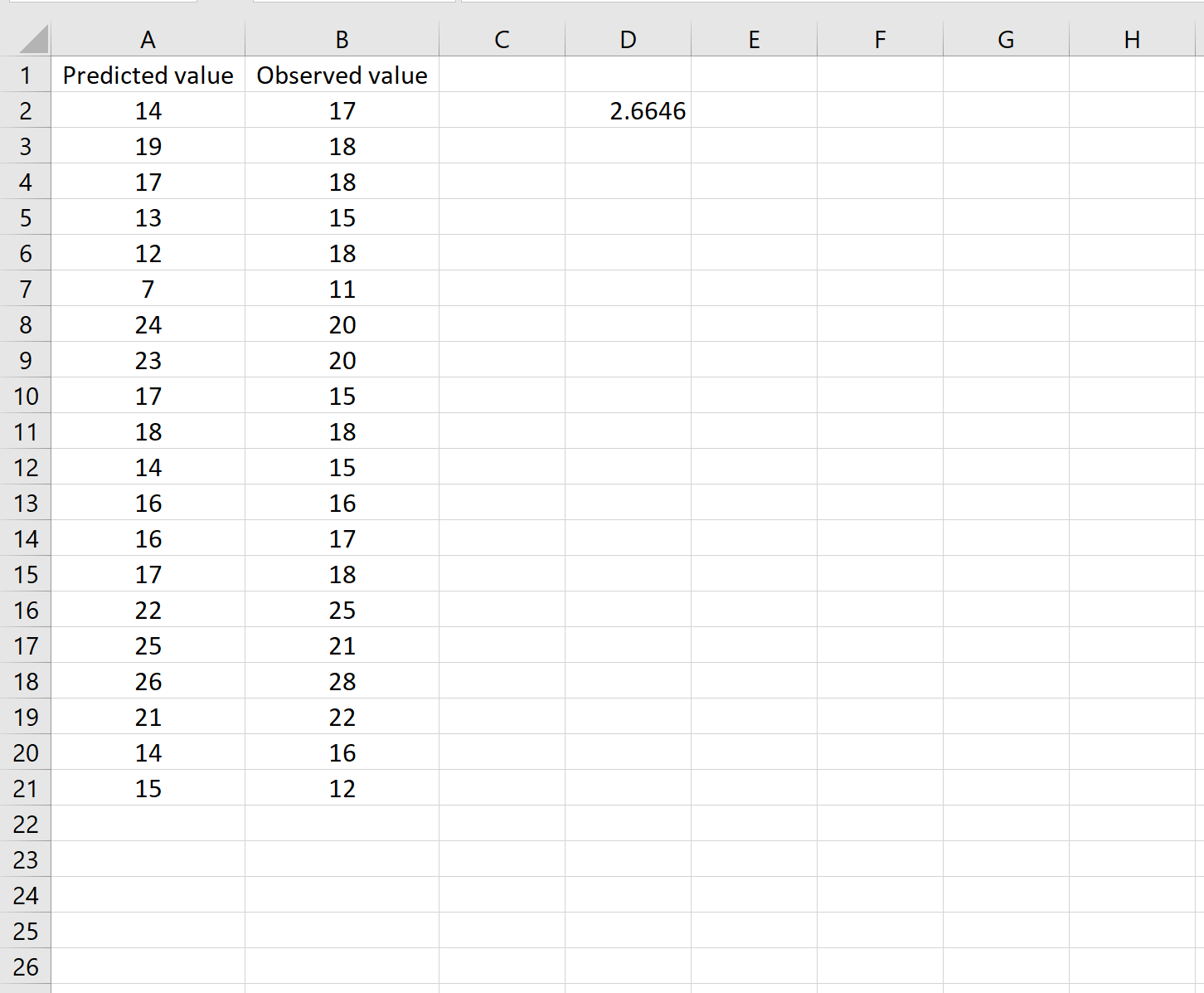
Cela nous indique que l’erreur quadratique moyenne est de 2,6646 .

La formule peut paraître un peu délicate, mais elle prend tout son sens une fois qu’on la décompose :

= SQRT( SUMSQ(A2:A21-B2:B21) / COMPTE(A2:A21) )

• Tout d’abord, nous calculons la somme des carrés des différences entre les valeurs prédites et observées à l’aide de la fonction SUMSQ() .
• Ensuite, nous divisons par la taille de l’échantillon de l’ensemble de données à l’aide de COUNTA() , qui compte le nombre de cellules d’une plage qui ne sont pas vides.
• Enfin, nous prenons la racine carrée de l’ensemble du calcul à l’aide de la fonction SQRT() .

Scénario 2

Dans un autre scénario, vous avez peut-être déjà calculé les différences entre les valeurs prédites et observées. Dans ce cas, vous n’aurez qu’une seule colonne affichant les différences.

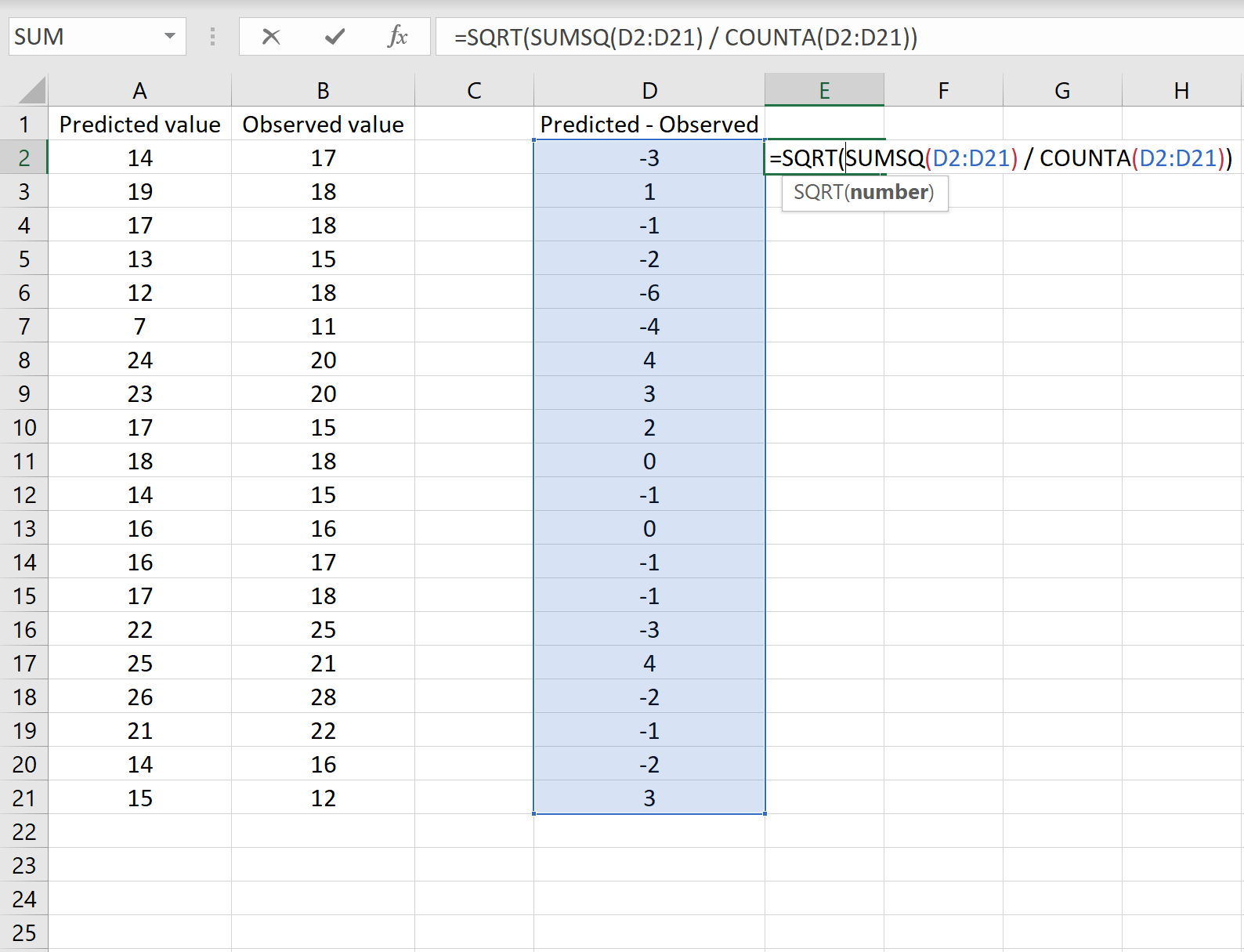
L’image ci-dessous montre un exemple de ce scénario. Les valeurs prédites sont affichées dans la colonne A, les valeurs observées dans la colonne B et la différence entre les valeurs prédites et observées dans la colonne D :

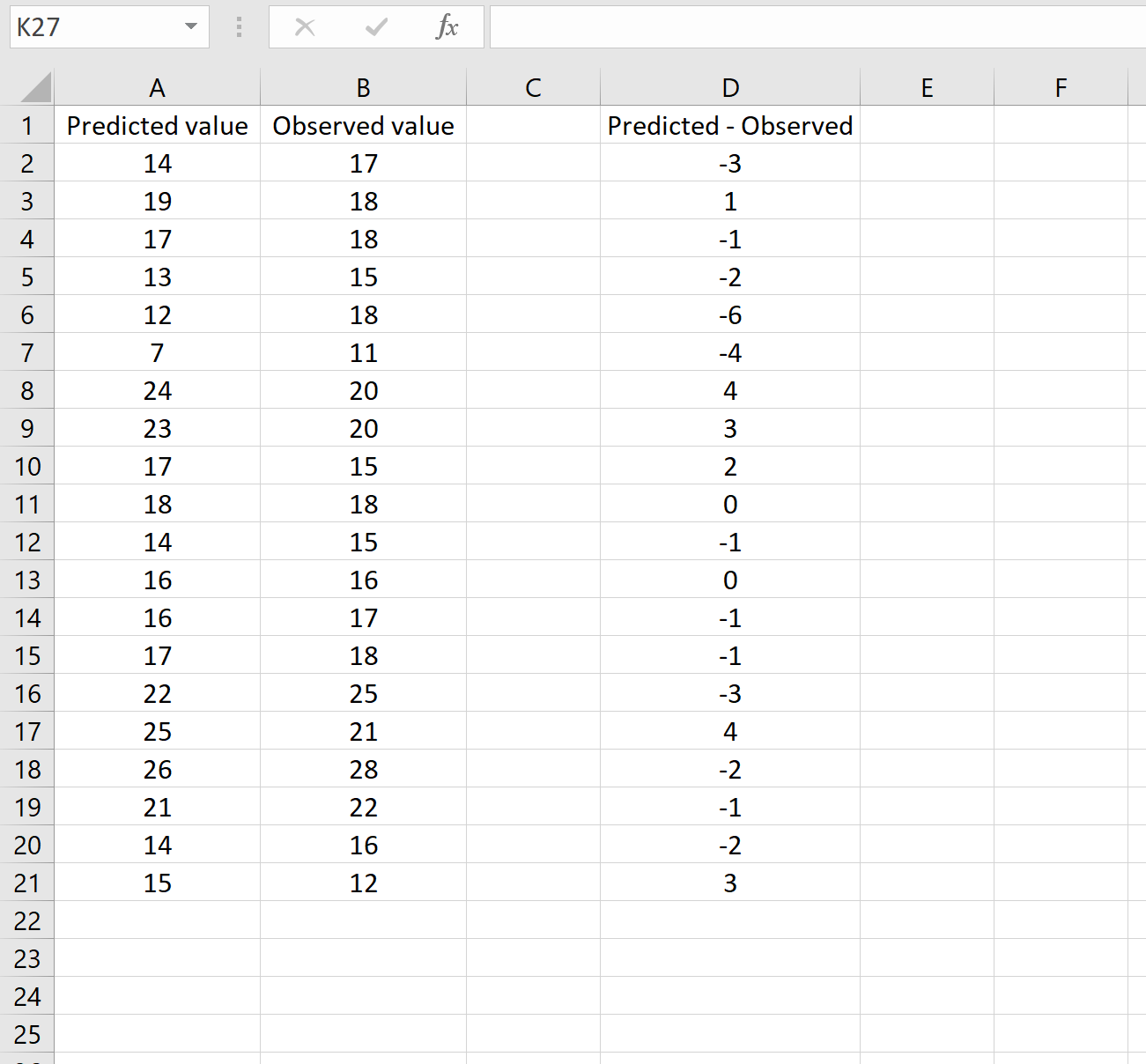
Si tel est le cas, vous pouvez calculer le RMSE en tapant la formule suivante dans n’importe quelle cellule, puis en cliquant sur CTRL+MAJ+ENTRÉE :

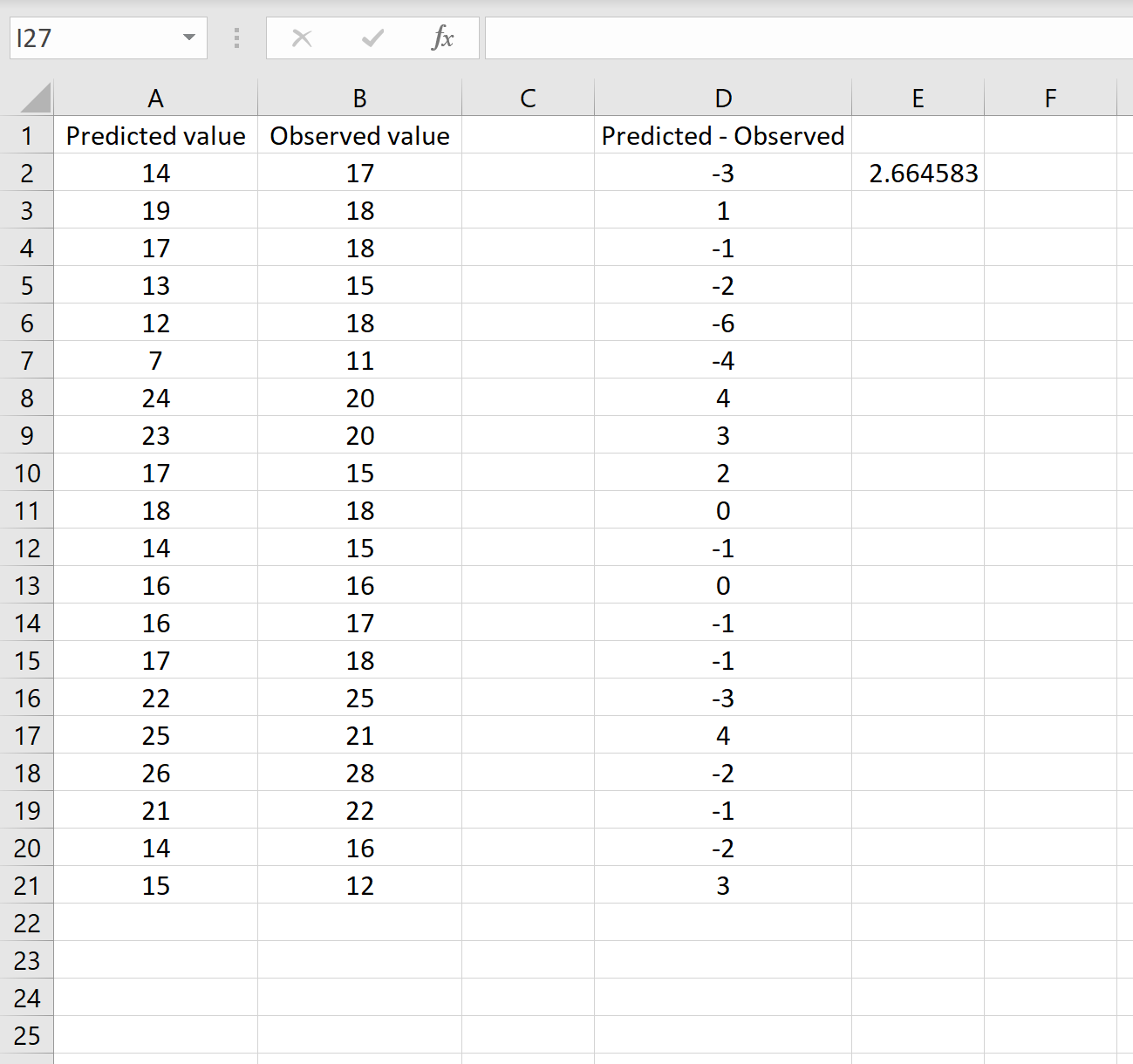
=SQRT(SUMSQ(D2:D21) / COMPTE(D2:D21))

Cela nous indique que l’erreur quadratique moyenne est de 2,6646 , ce qui correspond au résultat obtenu dans le premier scénario. Cela confirme que ces deux approches de calcul du RMSE sont équivalentes.

La formule que nous avons utilisée dans ce scénario n’est que légèrement différente de celle que nous avons utilisée dans le scénario précédent :

= SQRT( SUMSQ(D2:D21) / COMPTE(D2:D21) )

• Puisque nous avons déjà calculé les différences entre les valeurs prédites et observées dans la colonne D, nous pouvons calculer la somme des différences au carré en utilisant la fonction SUMSQ().   fonction avec uniquement les valeurs de la colonne D.
• Ensuite, nous divisons par la taille de l’échantillon de l’ensemble de données à l’aide de COUNTA() , qui compte le nombre de cellules d’une plage qui ne sont pas vides.
• Enfin, nous prenons la racine carrée de l’ensemble du calcul à l’aide de la fonction SQRT() .

Comment interpréter le RMSE

Comme mentionné précédemment, le RMSE est un moyen utile de voir dans quelle mesure un modèle de régression (ou tout modèle produisant des valeurs prédites) est capable de « s’adapter » à un ensemble de données.

Plus le RMSE est grand, plus la différence entre les valeurs prédites et observées est grande, ce qui signifie que moins le modèle de régression s’adapte aux données. À l’inverse, plus le RMSE est petit, plus le modèle est capable de s’adapter aux données.

Il peut être particulièrement utile de comparer le RMSE de deux modèles différents pour voir quel modèle correspond le mieux aux données.

Pour plus de didacticiels dans Excel, assurez-vous de consulter notre page des guides Excel , qui répertorie tous les didacticiels Excel sur la statologie.