Introduction à la régression au lasso

Dans la régression linéaire multiple ordinaire, nous utilisons un ensemble de p variables prédictives et une variable de réponse pour ajuster un modèle de la forme :

Y = β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p X _p + ε

où:

• Y : La variable de réponse
• X _j : la j ^ème variable prédictive
• β _j : L’effet moyen sur Y d’une augmentation d’une unité de X _j , en maintenant fixes tous les autres prédicteurs
• ε : Le terme d’erreur

Les valeurs de β ₀ , β ₁ , B ₂ , … , β _p sont choisies en utilisant la méthode des moindres carrés , qui minimise la somme des carrés des résidus (RSS) :

RSS = Σ(y _je – ŷ _je ) ²

où:

• Σ : Un symbole grec qui signifie somme
• y _i : la valeur de réponse réelle pour la ^ième observation
• ŷ _i : La valeur de réponse prédite basée sur le modèle de régression linéaire multiple

Cependant, lorsque les variables prédictives sont fortement corrélées, la multicolinéarité peut devenir un problème. Cela peut rendre les estimations des coefficients du modèle peu fiables et présenter une variance élevée. Autrement dit, lorsque le modèle est appliqué à un nouvel ensemble de données qu’il n’a jamais vu auparavant, il est susceptible de fonctionner de manière médiocre.

Une façon de contourner ce problème consiste à utiliser une méthode connue sous le nom de régression au lasso , qui cherche plutôt à minimiser les éléments suivants :

RSS + λΣ|β _j |

où j va de 1 à p et λ ≥ 0.

Ce deuxième terme de l’équation est connu sous le nom de pénalité de retrait .

Lorsque λ = 0, ce terme de pénalité n’a aucun effet et la régression au lasso produit les mêmes estimations de coefficient que les moindres carrés.

Cependant, à mesure que λ s’approche de l’infini, la pénalité de retrait devient plus influente et les variables prédictives qui ne sont pas importables dans le modèle sont réduites à zéro et certaines sont même supprimées du modèle.

Pourquoi utiliser la régression Lasso ?

L’avantage de la régression par lasso par rapport à la régression des moindres carrés réside dans le compromis biais-variance .

Rappelons que l’erreur quadratique moyenne (MSE) est une métrique que nous pouvons utiliser pour mesurer la précision d’un modèle donné et elle est calculée comme suit :

MSE = Var( f̂( x ₀ )) + [Biais( f̂( x ₀ ))] ² + Var(ε)

MSE = Variance + Biais ² + Erreur irréductible

L’idée de base de la régression au lasso est d’introduire un petit biais afin que la variance puisse être considérablement réduite, ce qui conduit à une MSE globale plus faible.

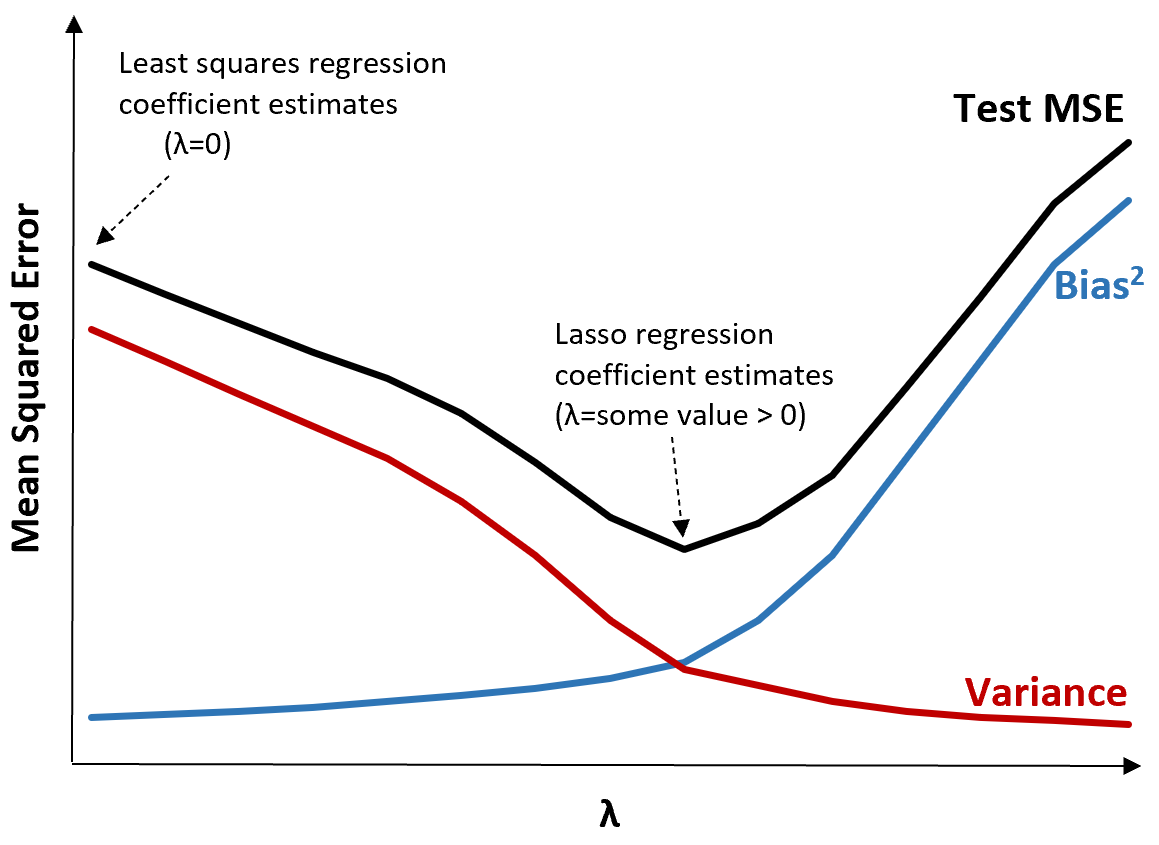
Pour illustrer cela, considérons le graphique suivant :

Notez que lorsque λ augmente, la variance diminue considérablement avec une très faible augmentation du biais. Cependant, au-delà d’un certain point, la variance diminue moins rapidement et la diminution des coefficients entraîne une sous-estimation significative de ceux-ci, ce qui entraîne une forte augmentation du biais.

Nous pouvons voir sur le graphique que le MSE du test est le plus bas lorsque nous choisissons une valeur pour λ qui produit un compromis optimal entre biais et variance.

Lorsque λ = 0, le terme de pénalité dans la régression au lasso n’a aucun effet et produit donc les mêmes estimations de coefficient que les moindres carrés. Cependant, en augmentant λ jusqu’à un certain point, nous pouvons réduire le MSE global du test.

Cela signifie que l’ajustement du modèle par régression au lasso produira des erreurs de test plus petites que l’ajustement du modèle par régression des moindres carrés.

Régression Lasso vs régression Ridge

La régression Lasso et la régression Ridge sont toutes deux connues sous le nom de méthodes de régularisation car elles tentent toutes deux de minimiser la somme des carrés résiduels (RSS) ainsi qu’un certain terme de pénalité.

En d’autres termes, ils contraignent ou régularisent les estimations des coefficients du modèle.

Cependant, les termes de pénalité qu’ils utilisent sont un peu différents :

• La régression lasso tente de minimiser RSS + λΣ|β _j |
• La régression Ridge tente de minimiser RSS + λΣβ _j ²

Lorsque nous utilisons la régression de crête, les coefficients de chaque prédicteur sont réduits à zéro mais aucun d’entre eux ne peut aller complètement à zéro .

À l’inverse, lorsque nous utilisons la régression par lasso, il est possible que certains coefficients deviennent complètement nuls lorsque λ devient suffisamment grand.

En termes techniques, la régression par lasso est capable de produire des modèles « clairsemés », c’est-à-dire des modèles qui n’incluent qu’un sous-ensemble de variables prédictives.

Cela soulève la question suivante : la régression par crête ou la régression par lasso est-elle meilleure ?

La réponse : ça dépend !

Dans les cas où seul un petit nombre de variables prédictives sont significatives, la régression par lasso a tendance à mieux fonctionner car elle est capable de réduire complètement les variables insignifiantes à zéro et de les supprimer du modèle.

Cependant, lorsque de nombreuses variables prédictives sont significatives dans le modèle et que leurs coefficients sont à peu près égaux, la régression de crête a tendance à mieux fonctionner car elle conserve tous les prédicteurs dans le modèle.

Pour déterminer quel modèle est le plus efficace pour faire des prédictions, nous effectuons une validation croisée k fois . Quel que soit le modèle qui produit l’erreur quadratique moyenne (MSE) la plus faible, il est préférable d’utiliser le modèle à utiliser.

Étapes pour effectuer une régression au lasso en pratique

Les étapes suivantes peuvent être utilisées pour effectuer une régression au lasso :

Étape 1 : Calculez la matrice de corrélation et les valeurs VIF pour les variables prédictives.

Tout d’abord, nous devons produire une matrice de corrélation et calculer les valeurs VIF (variance inflation factor) pour chaque variable prédictive.

Si nous détectons une forte corrélation entre les variables prédictives et les valeurs VIF élevées (certains textes définissent une valeur VIF « élevée » comme 5 tandis que d’autres utilisent 10), alors la régression par lasso est probablement appropriée.

Cependant, s’il n’y a pas de multicolinéarité dans les données, il n’est peut-être pas nécessaire d’effectuer une régression au lasso en premier lieu. Au lieu de cela, nous pouvons effectuer une régression des moindres carrés ordinaires.

Étape 2 : Ajustez le modèle de régression du lasso et choisissez une valeur pour λ.

Une fois que nous avons déterminé que la régression par lasso est appropriée, nous pouvons ajuster le modèle (en utilisant des langages de programmation populaires comme R ou Python) en utilisant la valeur optimale pour λ.

Pour déterminer la valeur optimale pour λ, nous pouvons ajuster plusieurs modèles en utilisant différentes valeurs pour λ et choisir λ comme valeur qui produit le MSE de test le plus bas.

Étape 3 : Comparez la régression du lasso à la régression des crêtes et à la régression des moindres carrés ordinaires.

Enfin, nous pouvons comparer notre modèle de régression au lasso à un modèle de régression de crête et à un modèle de régression des moindres carrés pour déterminer quel modèle produit le MSE de test le plus bas en utilisant la validation croisée k fois.

Selon la relation entre les variables prédictives et la variable de réponse, il est tout à fait possible que l’un de ces trois modèles surpasse les autres dans différents scénarios.

Régression Lasso en R & Python

Les didacticiels suivants expliquent comment effectuer une régression au lasso dans R et Python :

Régression Lasso dans R (étape par étape)
Régression Lasso en Python (étape par étape)