Qu’est-ce que la régression curviligne ? (Définition & Exemples)
La régression curviligne est le nom donné à tout modèle de régression qui tente d’ajuster une courbe plutôt qu’une ligne droite.
Des exemples courants de modèles de régression curviligne incluent :
Régression quadratique : utilisée lorsqu’une relation quadratique existe entre une variable prédictive et une variable de réponse . Lorsqu’il est représenté graphiquement, ce type de relation ressemble à un « U » ou à un « U » inversé sur un nuage de points :
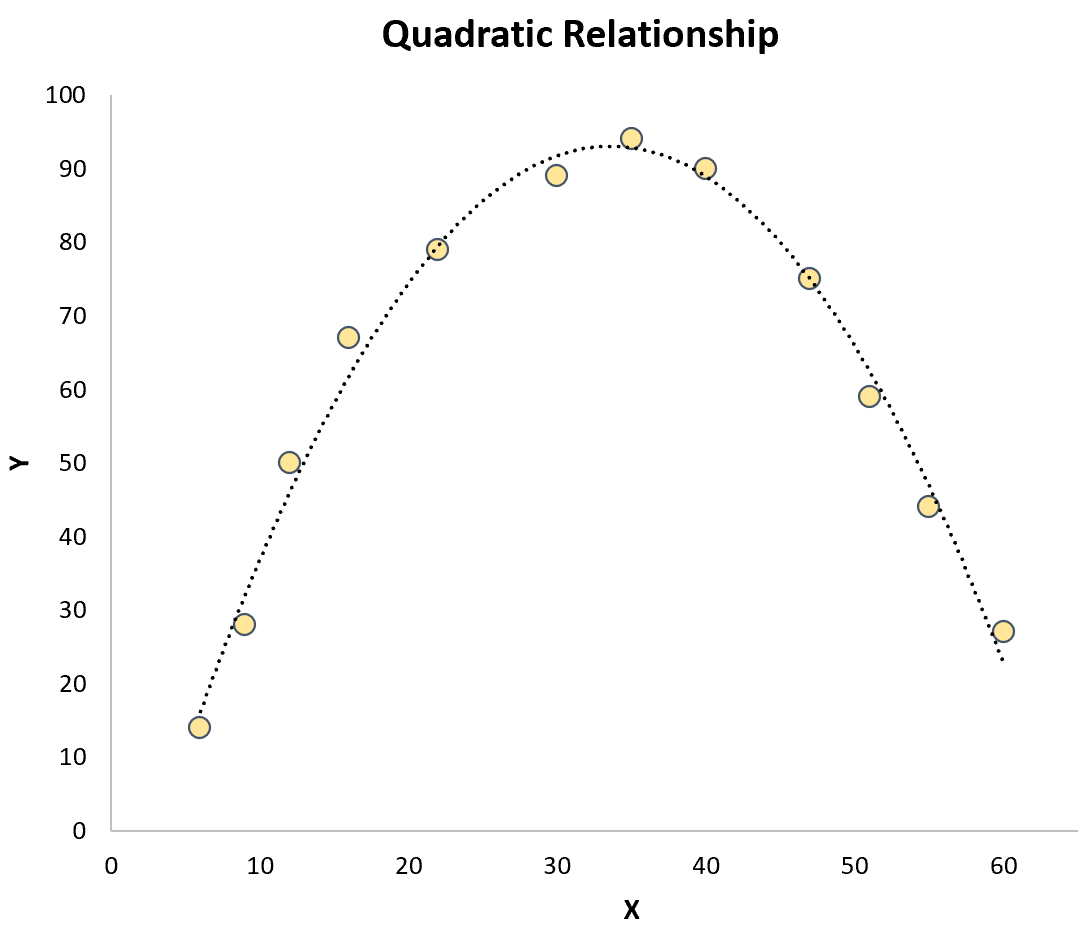
Régression cubique : utilisée lorsqu’une relation cubique existe entre une variable prédictive et une variable de réponse. Lorsqu’elle est représentée graphiquement, ce type de relation présente deux courbes distinctes sur un nuage de points :
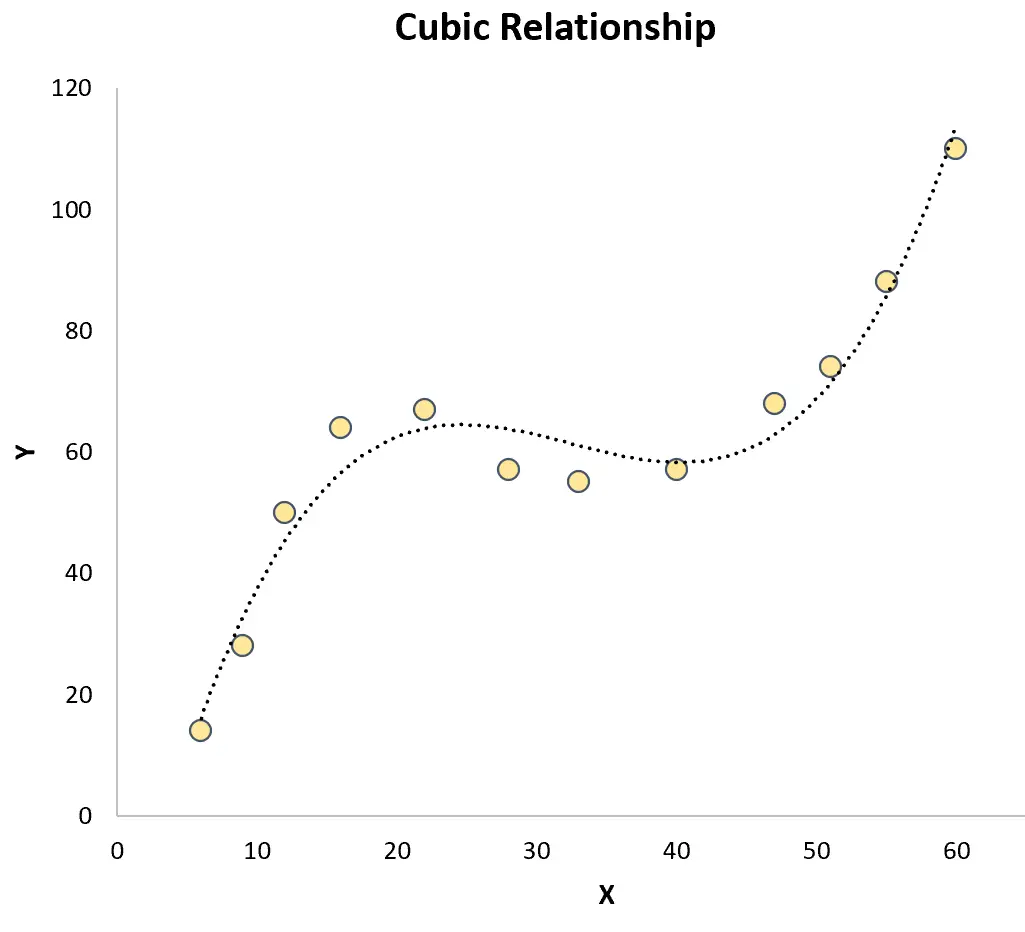
Ces deux éléments contrastent avec la régression linéaire simple dans laquelle la relation entre la variable prédictive et la variable de réponse est linéaire :
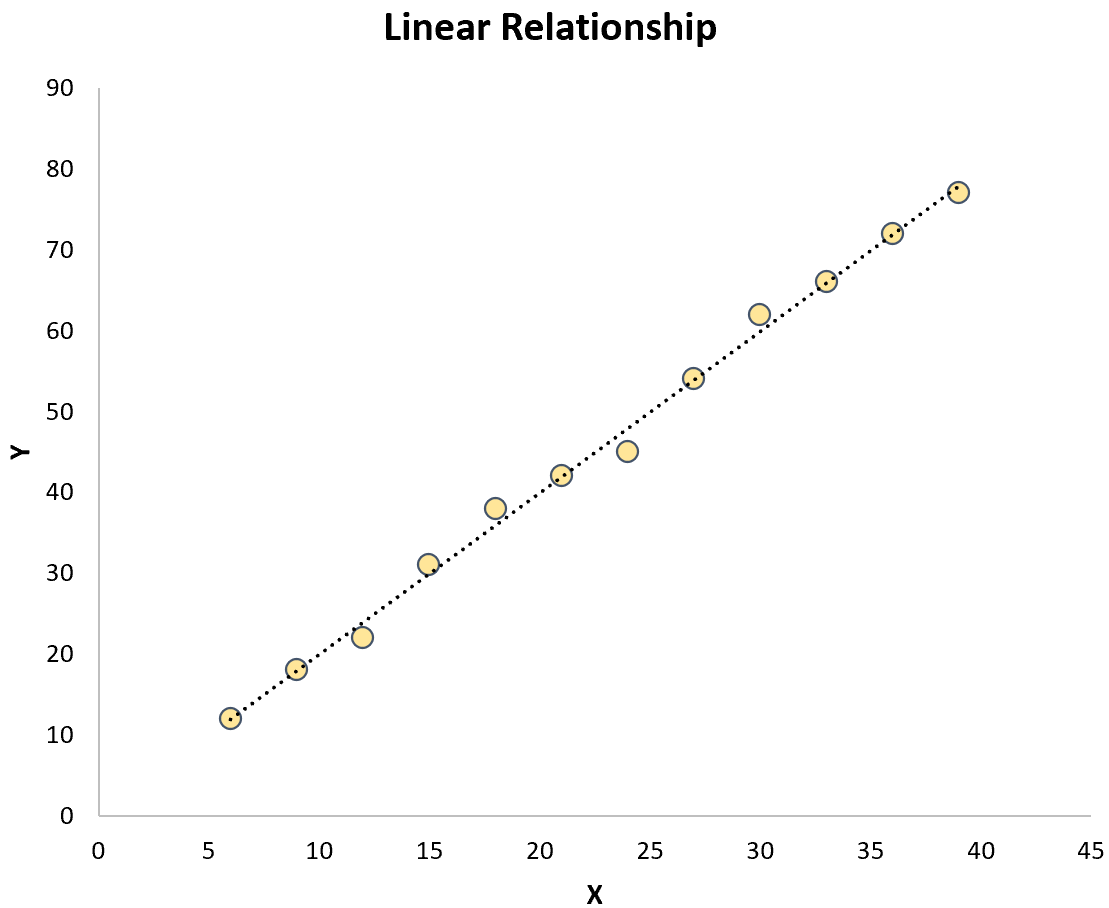
La formule des modèles de régression curviligne
Un modèle de régression linéaire simple tente d’ajuster un ensemble de données à l’aide de la formule suivante :
ŷ = β 0 + β 1 x
où:
- ŷ : La variable de réponse
- β 0 , β 1 : Les coefficients de régression
- x : la variable prédictive
En revanche, un modèle de régression quadratique utilise la formule suivante :
ŷ = β 0 + β 1 x + β 2 x 2
Et un modèle de régression cubique utilise la formule suivante :
ŷ = β 0 + β 1 x + β 2 x 2 + β 3 x 3
Un nom plus général donné aux modèles de régression qui incluent des exposants est régression polynomiale , qui prend la formule suivante :
ŷ = β 0 + β 1 x + β 2 x 2 + … + β k x k
La valeur de k indique le degré du polynôme. Bien que le degré puisse être n’importe quel nombre positif, dans la pratique, nous ajustons rarement des modèles de régression polynomiale avec un degré supérieur à 3 ou 4.
En utilisant des exposants dans la formule du modèle de régression, les modèles de régression polynomiale sont capables d’ajuster des courbes aux ensembles de données au lieu de lignes droites.
Quand utiliser la régression curviligne
Le moyen le plus simple de savoir si vous devez ou non utiliser la régression curviligne est de créer un nuage de points de la variable prédictive et de la variable de réponse.
Si le nuage de points affiche une relation linéaire entre les deux variables, une régression linéaire simple est probablement appropriée.
Cependant, si le nuage de points montre un motif quadratique, cubique ou autre motif curviligne entre le prédicteur et la variable de réponse, alors la régression curviligne est probablement plus appropriée à utiliser.
Vous pouvez également ajuster un modèle de régression linéaire simple et un modèle de régression curviligne et comparer les valeurs R au carré ajustées de chaque modèle pour déterminer quel modèle offre le meilleur ajustement aux données.
Le R-carré ajusté est utile car il vous indique la proportion de la variance de la variable de réponse qui peut être expliquée par la ou les variables prédictives, ajustées en fonction du nombre de variables prédictives dans le modèle.
En général, le modèle avec la valeur R carré ajustée la plus élevée offre un meilleur ajustement à l’ensemble de données.
Ressources additionnelles
Les didacticiels suivants expliquent comment effectuer une régression polynomiale dans différents logiciels statistiques :
Une introduction à la régression polynomiale
Comment effectuer une régression polynomiale dans Excel
Comment effectuer une régression polynomiale en Python
Comment effectuer une régression polynomiale dans R
à propos de l'auteur
Dr. Benjamin Anderson
Il est un professeur de statistiques à la retraite devenu éducateur dévoué sur Statorials. Avec une vaste expérience et une expertise dans le domaine des statistiques, je m'engage à partager mes connaissances pour responsabiliser les étudiants grâce à Statorials. Lire plus