Régression exponentielle dans R (étape par étape)

La régression exponentielle est un type de régression qui peut être utilisé pour modéliser les situations suivantes :

1. Croissance exponentielle : La croissance commence lentement puis s’accélère rapidement et sans limite.

2. Décroissance exponentielle : La décroissance commence rapidement puis ralentit pour se rapprocher de plus en plus de zéro.

L’équation d’un modèle de régression exponentielle prend la forme suivante :

y = ab ^x

où:

• y : la variable de réponse
• x : la variable prédictive
• a, b : les coefficients de régression qui décrivent la relation entre x et y

L’exemple étape par étape suivant montre comment effectuer une régression exponentielle dans R.

Étape 1 : Créer les données

Tout d’abord, créons de fausses données pour deux variables : x et y :

x=1:20
y=c(1, 3, 5, 7, 9, 12, 15, 19, 23, 28, 33, 38, 44, 50, 56, 64, 73, 84, 97, 113)

Étape 2 : Visualisez les données

Créons ensuite un nuage de points rapide pour visualiser la relation entre x et y :

plot(x, y)

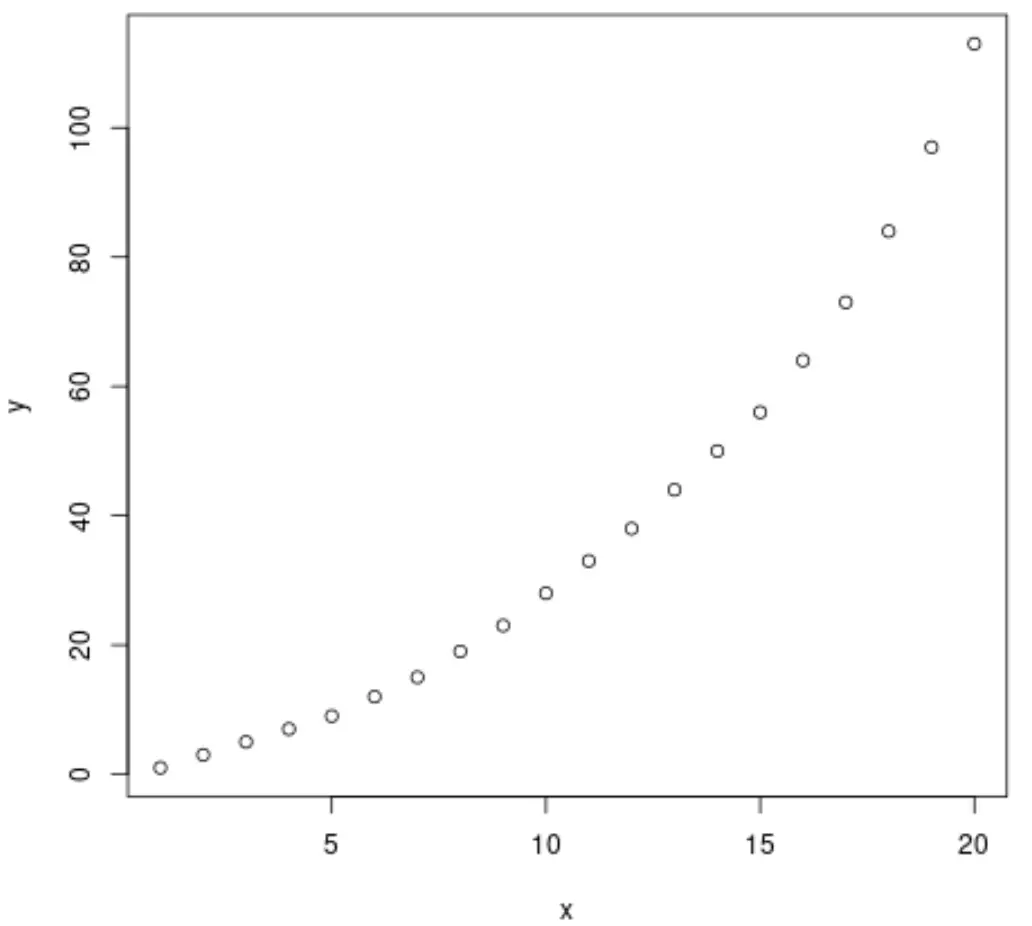
D’après le graphique, nous pouvons voir qu’il existe un schéma de croissance exponentielle clair entre les deux variables.

Il semble donc judicieux d’ajuster une équation de régression exponentielle pour décrire la relation entre les variables.

Étape 3 : Ajuster le modèle de régression exponentielle

Ensuite, nous utiliserons la fonction lm() pour ajuster un modèle de régression exponentielle, en utilisant le logarithme naturel de y comme variable de réponse et x comme variable prédictive :

#fit the model
model <- lm(log(y)~ x)

#view the output of the model
summary(model)

Call:
lm(formula = log(y) ~ x)

Residuals:
    Min      1Q  Median      3Q     Max 
-1.1858 -0.1768  0.1104  0.2720  0.3300 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.98166    0.17118   5.735 1.95e-05 ***
x            0.20410    0.01429  14.283 2.92e-11 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.3685 on 18 degrees of freedom
Multiple R-squared:  0.9189,	Adjusted R-squared:  0.9144 
F-statistic:   204 on 1 and 18 DF,  p-value: 2.917e-11

La valeur F globale du modèle est de 204 et la valeur p correspondante est extrêmement faible (2,917e-11), ce qui indique que le modèle dans son ensemble est utile.

En utilisant les coefficients du tableau de sortie, nous pouvons voir que l’équation de régression exponentielle ajustée est :

ln(y) = 0,9817 + 0,2041(x)

En appliquant e aux deux côtés, nous pouvons réécrire l’équation comme suit :

y = 2,6689 * ^1,2264x

Nous pouvons utiliser cette équation pour prédire la variable de réponse, y , en fonction de la valeur de la variable prédictive, x . Par exemple, si x = 12, alors nous prédirions que y serait 30,897 :

y = 2,6689 * 1,2264 ¹² = 30,897

Bonus : n’hésitez pas à utiliser ce calculateur de régression exponentielle en ligne pour calculer automatiquement l’équation de régression exponentielle pour un prédicteur et une variable de réponse donnés.

Ressources additionnelles

Comment effectuer une régression linéaire simple dans R
Comment effectuer une régression linéaire multiple dans R
Comment effectuer une régression quadratique dans R
Comment effectuer une régression polynomiale dans R