Comment effectuer une régression linéaire dans Google Sheets

La régression linéaire est une méthode qui peut être utilisée pour quantifier la relation entre une ou plusieurs variables explicatives et une variable de réponse .

Nous utilisons la régression linéaire simple lorsqu’il n’y a qu’une seule variable explicative et la régression linéaire multiple lorsqu’il y a deux variables explicatives ou plus.

Il est possible d’effectuer les deux types de régressions à l’aide de la fonction LINEST() de Google Sheets, qui utilise la syntaxe suivante :

LINEST (known_data_y, known_data_x, calculate_b, verbeux)

où:

• known_data_y : tableau de valeurs de réponse
• known_data_x : Tableau de valeurs explicatives
• calculate_b : indique s’il faut ou non calculer l’ordonnée à l’origine. C’est VRAI par défaut et nous le laissons ainsi pour la régression linéaire.
• verbeux : indique s’il faut ou non fournir des statistiques de régression supplémentaires au-delà de la seule pente et de l’interception. C’est FAUX par défaut, mais nous préciserons que c’est VRAI dans nos exemples.

Les exemples suivants montrent comment utiliser cette fonction dans la pratique.

Régression linéaire simple dans Google Sheets

Supposons que nous souhaitions comprendre la relation entre les heures étudiées et les résultats de l’examen. études en vue d’un examen et la note obtenue à l’examen.

Pour explorer cette relation, nous pouvons effectuer une régression linéaire simple en utilisant les heures étudiées comme variable explicative et les résultats à l’examen comme variable de réponse.

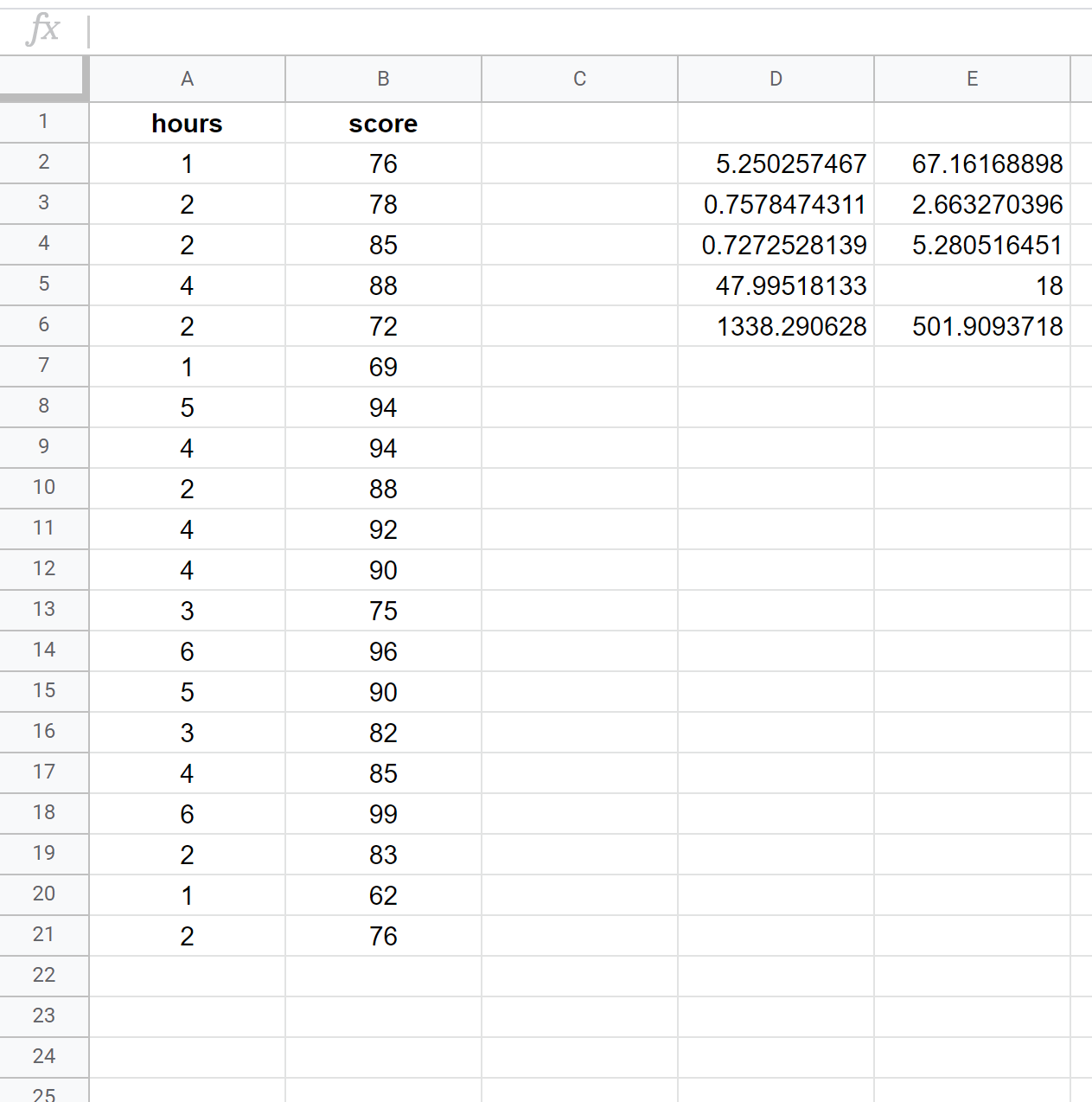
La capture d’écran suivante montre comment effectuer une régression linéaire simple à l’aide d’un ensemble de données de 20 étudiants avec la formule suivante utilisée dans la cellule D2 :

= LIGNE ( B2:B21 , A2:A21 , VRAI , VRAI )

La capture d’écran suivante fournit des annotations pour la sortie :

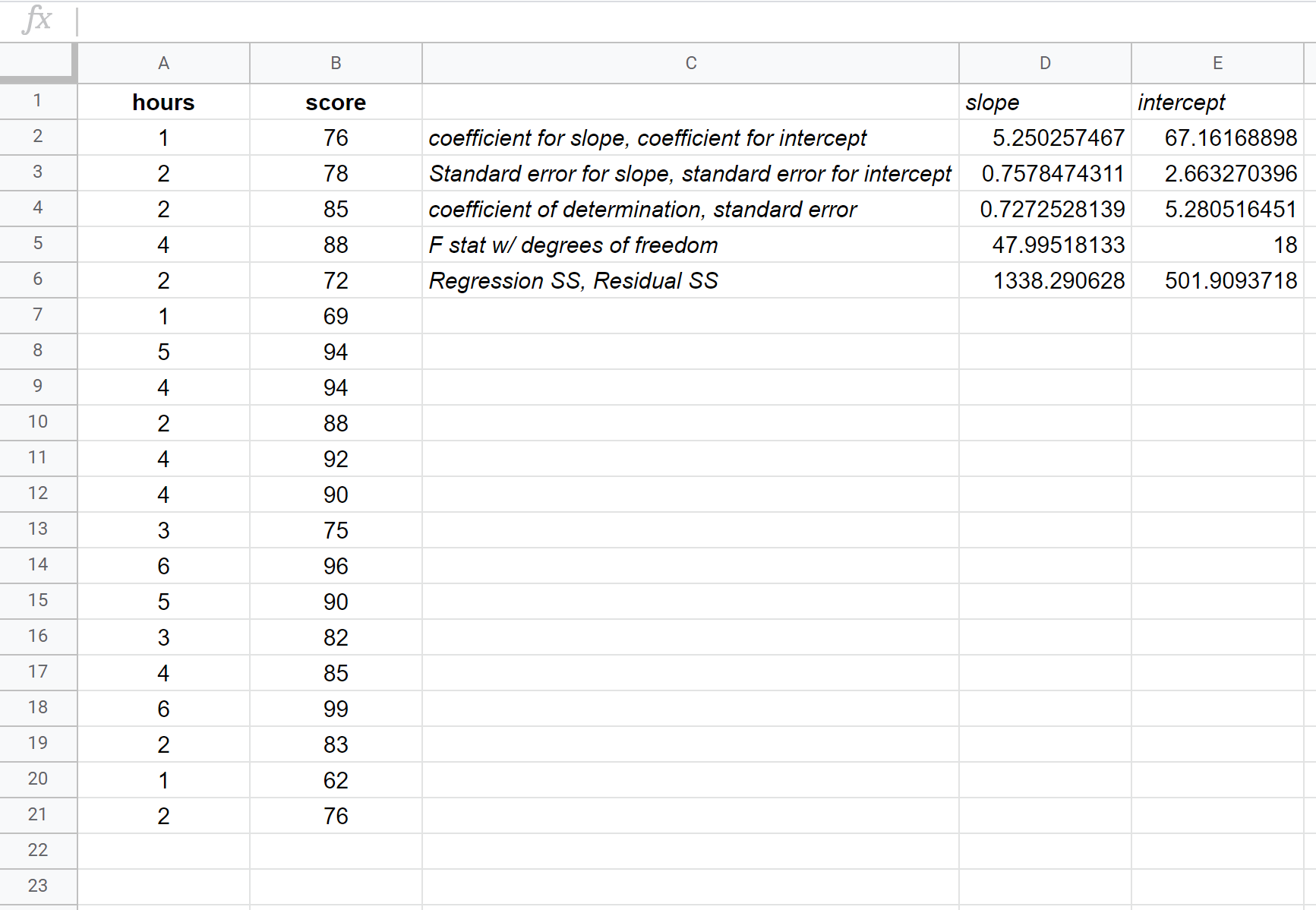
Voici comment interpréter les nombres les plus pertinents dans le résultat :

R Carré : 0,72725 . C’est ce qu’on appelle le coefficient de détermination. C’est la proportion de la variance de la variable de réponse qui peut être expliquée par la variable explicative. Dans cet exemple, environ 72,73 % de la variation des résultats des examens peut s’expliquer par le nombre d’heures étudiées.

Erreur type : 5,2805 . Il s’agit de la distance moyenne entre les valeurs observées et la droite de régression. Dans cet exemple, les valeurs observées s’éloignent en moyenne de 5,2805 unités de la droite de régression.

Coefficients : Les coefficients nous donnent les nombres nécessaires pour écrire l’équation de régression estimée. Dans cet exemple, l’équation de régression estimée est :

Note à l’examen = 67,16 + 5,2503*(heures)

Nous interprétons le coefficient des heures comme signifiant que pour chaque heure supplémentaire étudiée, la note à l’examen devrait augmenter de 5,2503 en moyenne. Nous interprétons le coefficient de l’interception comme signifiant que la note attendue à l’examen pour un étudiant qui étudie zéro heure est de 67,16 .

Nous pouvons utiliser cette équation de régression estimée pour calculer la note attendue à l’examen pour un étudiant, en fonction du nombre d’heures d’études. Par exemple, un étudiant qui étudie pendant trois heures devrait obtenir une note à l’examen de 82,91 :

Note à l’examen = 67,16 + 5,2503*(3) = 82,91

Régression linéaire multiple dans Google Sheets

Supposons que nous voulions savoir si le nombre d’heures passées à étudier et le nombre d’examens préparatoires passés affectent la note qu’un étudiant obtient à un certain examen d’entrée à l’université.

Pour explorer cette relation, nous pouvons effectuer une régression linéaire multiple en utilisant les heures étudiées et les examens préparatoires passés comme variables explicatives et les résultats de l’examen comme variable de réponse.

La capture d’écran suivante montre comment effectuer une régression linéaire multiple à l’aide d’un ensemble de données de 20 étudiants avec la formule suivante utilisée dans la cellule E2 :

= DROITE ( C2:C21 , A2:B21 , VRAI , VRAI )

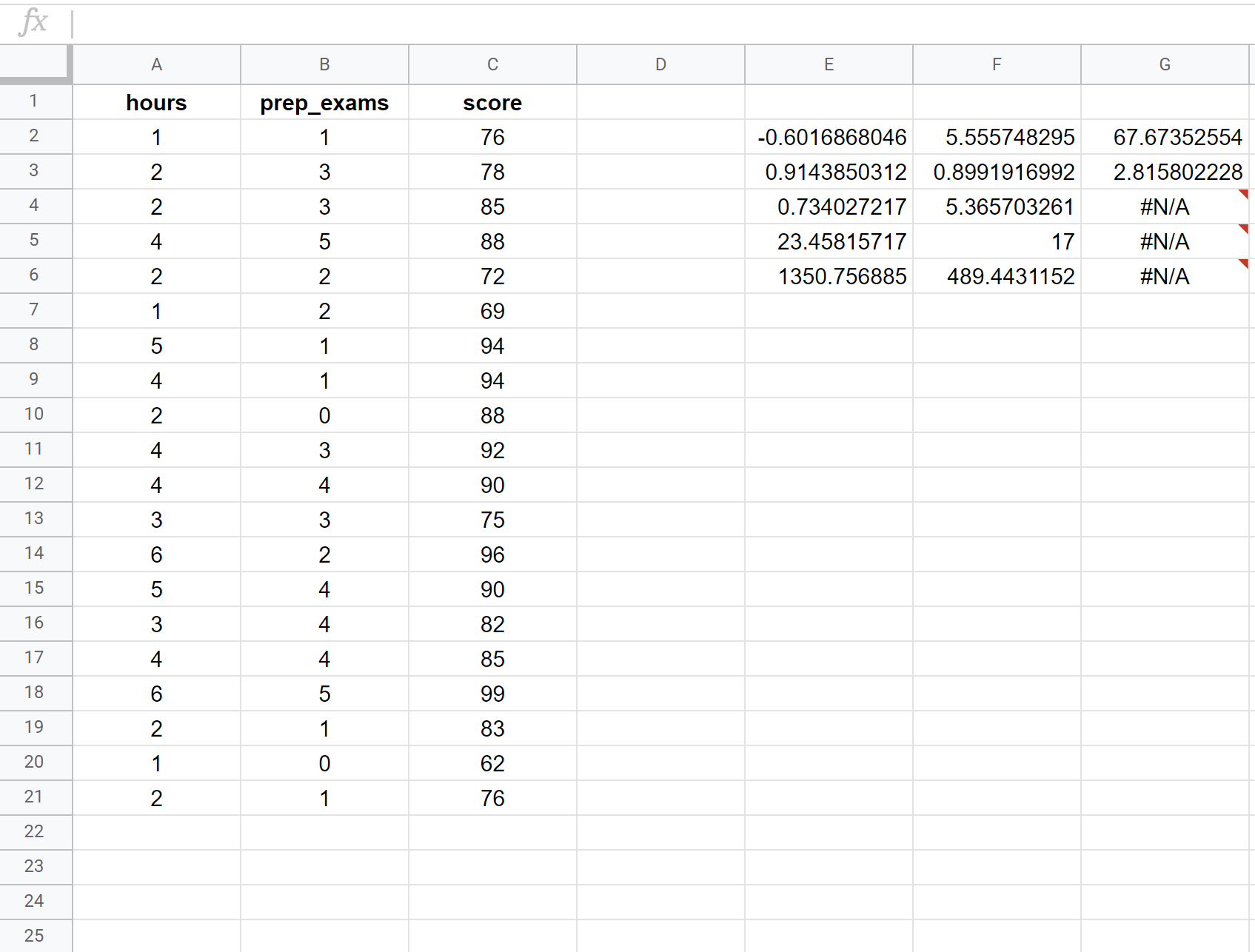
Voici comment interpréter les nombres les plus pertinents dans le résultat :

R Carré : 0,734 . C’est ce qu’on appelle le coefficient de détermination. C’est la proportion de la variance de la variable de réponse qui peut être expliquée par les variables explicatives. Dans cet exemple, 73,4 % de la variation des résultats aux examens s’explique par le nombre d’heures étudiées et le nombre d’examens préparatoires passés.

Erreur type : 5,3657 . Il s’agit de la distance moyenne entre les valeurs observées et la droite de régression. Dans cet exemple, les valeurs observées s’éloignent en moyenne de 5,3657 unités de la droite de régression.

Équation de régression estimée : nous pouvons utiliser les coefficients de la sortie du modèle pour créer l’équation de régression estimée suivante :

Note à l’examen = 67,67 + 5,56*(heures) – 0,60*(examens préparatoires)

Nous pouvons utiliser cette équation de régression estimée pour calculer la note attendue à l’examen pour un étudiant, en fonction du nombre d’heures d’étude et du nombre d’examens préparatoires qu’il passe. Par exemple, un étudiant qui étudie pendant trois heures et passe un examen préparatoire devrait obtenir une note de 83,75 :

Note à l’examen = 67,67 + 5,56*(3) – 0,60*(1) = 83,75

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes dans Google Sheets :

Comment effectuer une régression polynomiale dans Google Sheets
Comment créer un tracé résiduel dans Google Sheets