Régression linéaire multiple à la main (étape par étape)
La régression linéaire multiple est une méthode que nous pouvons utiliser pour quantifier la relation entre deux ou plusieurs variables prédictives et une variable de réponse .
Ce didacticiel explique comment effectuer manuellement une régression linéaire multiple.
Exemple : régression linéaire multiple à la main
Supposons que nous ayons l’ensemble de données suivant avec une variable de réponse y et deux variables prédictives X 1 et X 2 :
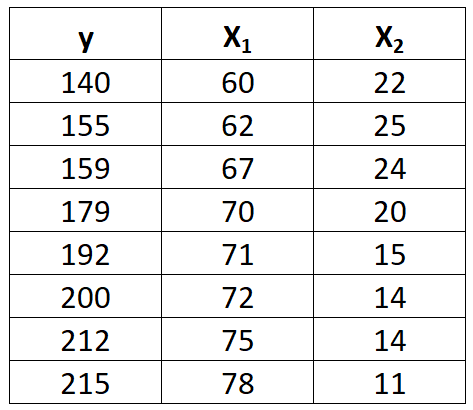
Suivez les étapes suivantes pour adapter un modèle de régression linéaire multiple à cet ensemble de données.
Étape 1 : Calculez X 1 2 , X 2 2 , X 1 y, X 2 y et X 1 X 2 .
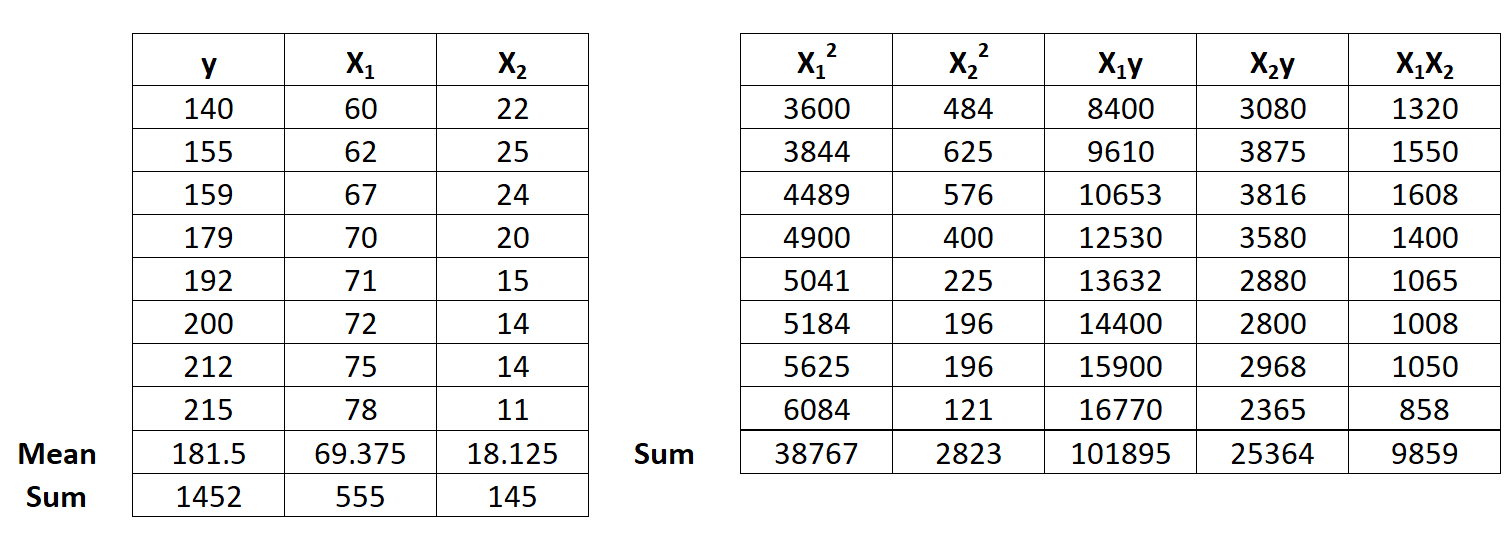
Étape 2 : Calculez les sommes de régression.
Ensuite, effectuez les calculs de somme de régression suivants :
- Σ x 1 2 = Σ X 1 2 – (ΣX 1 ) 2 / n = 38 767 – (555) 2 / 8 = 263,875
- Σ x 2 2 = Σ X 2 2 – (ΣX 2 ) 2 / n = 2 823 – (145) 2 / 8 = 194,875
- Σ x 1 y = Σ X 1 y – (ΣX 1 Σy) / n = 101 895 – (555*1 452) / 8 = 1 162,5
- Σ x 2 y = Σ X 2 y – (ΣX 2 Σy) / n = 25 364 – (145*1 452) / 8 = -953,5
- Σ x 1 x 2 = Σ X 1 X 2 – (ΣX 1 ΣX 2 ) / n = 9 859 – (555*145) / 8 = -200,375
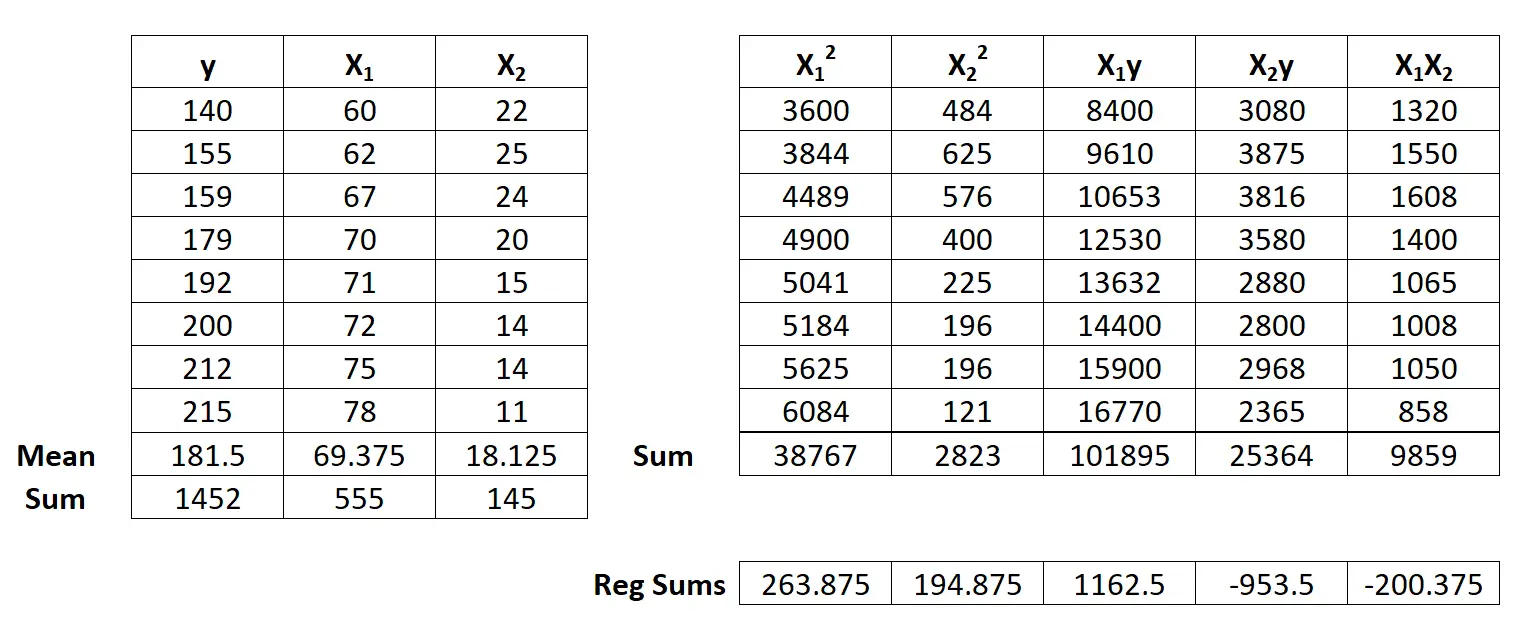
Étape 3 : Calculez b 0 , b 1 et b 2 .
La formule pour calculer b 1 est : [(Σx 2 2 )(Σx 1 y) – (Σx 1 x 2 )(Σx 2 y)] / [(Σx 1 2 ) (Σx 2 2 ) – (Σx 1 x 2 ) 2 ]
Ainsi, b 1 = [(194,875)(1162,5) – (-200,375)(-953,5)] / [(263,875) (194,875) – (-200,375) 2 ] = 3,148
La formule pour calculer b 2 est : [(Σx 1 2 )(Σx 2 y) – (Σx 1 x 2 )(Σx 1 y)] / [(Σx 1 2 ) (Σx 2 2 ) – (Σx 1 x 2 ) 2 ]
Ainsi, b 2 = [(263,875)(-953,5) – (-200,375)(1152,5)] / [(263,875) (194,875) – (-200,375) 2 ] = -1,656
La formule pour calculer b 0 est : y – b 1 X 1 – b 2 X 2
Ainsi, b 0 = 181,5 – 3,148(69,375) – (-1,656)(18,125) = -6,867
Étape 5 : placez b 0 , b 1 et b 2 dans l’équation de régression linéaire estimée.
L’équation de régression linéaire estimée est la suivante : ŷ = b 0 + b 1 *x 1 + b 2 *x 2
Dans notre exemple, c’est ŷ = -6,867 + 3,148x 1 – 1,656x 2
Comment interpréter une équation de régression linéaire multiple
Voici comment interpréter cette équation de régression linéaire estimée : ŷ = -6,867 + 3,148x 1 – 1,656x 2
b 0 = -6,867 . Lorsque les deux variables prédictives sont égales à zéro, la valeur moyenne de y est de -6,867.
b 1 = 3,148 . Une augmentation d’une unité de x 1 est associée à une augmentation de 3,148 unités de y, en moyenne, en supposant que x 2 reste constant.
b 2 = -1,656 . Une augmentation d’une unité de x 2 est associée à une diminution de 1,656 unité de y, en moyenne, en supposant que x 1 reste constant.
Ressources additionnelles
Une introduction à la régression linéaire multiple
Comment effectuer une régression linéaire simple à la main
