Comment effectuer une régression linéaire multiple dans SAS
La régression linéaire multiple est une méthode que nous pouvons utiliser pour comprendre la relation entre deux ou plusieurs variables prédictives et une variable de réponse .
Ce didacticiel explique comment effectuer une régression linéaire multiple dans SAS.
Étape 1 : Créer les données
Supposons que nous souhaitions adapter un modèle de régression linéaire multiple qui utilise le nombre d’heures passées à étudier et le nombre d’examens préparatoires passés pour prédire la note finale des étudiants à l’examen :
Score de l’examen = β 0 + β 1 (heures) + β 2 (examens préparatoires)
Tout d’abord, nous allons utiliser le code suivant pour créer un ensemble de données contenant ces informations pour 20 étudiants :
/*create dataset*/ data exam_data; input hours prep_exams score; datalines; 1 1 76 2 3 78 2 3 85 4 5 88 2 2 72 1 2 69 5 1 94 4 1 94 2 0 88 4 3 92 4 4 90 3 3 75 6 2 96 5 4 90 3 4 82 4 4 85 6 5 99 2 1 83 1 0 62 2 1 76 ; run;
Étape 2 : Effectuer une régression linéaire multiple
Ensuite, nous utiliserons proc reg pour ajuster un modèle de régression linéaire multiple aux données :
/*fit multiple linear regression model*/ proc reg data=exam_data; model score = hours prep_exams; run;
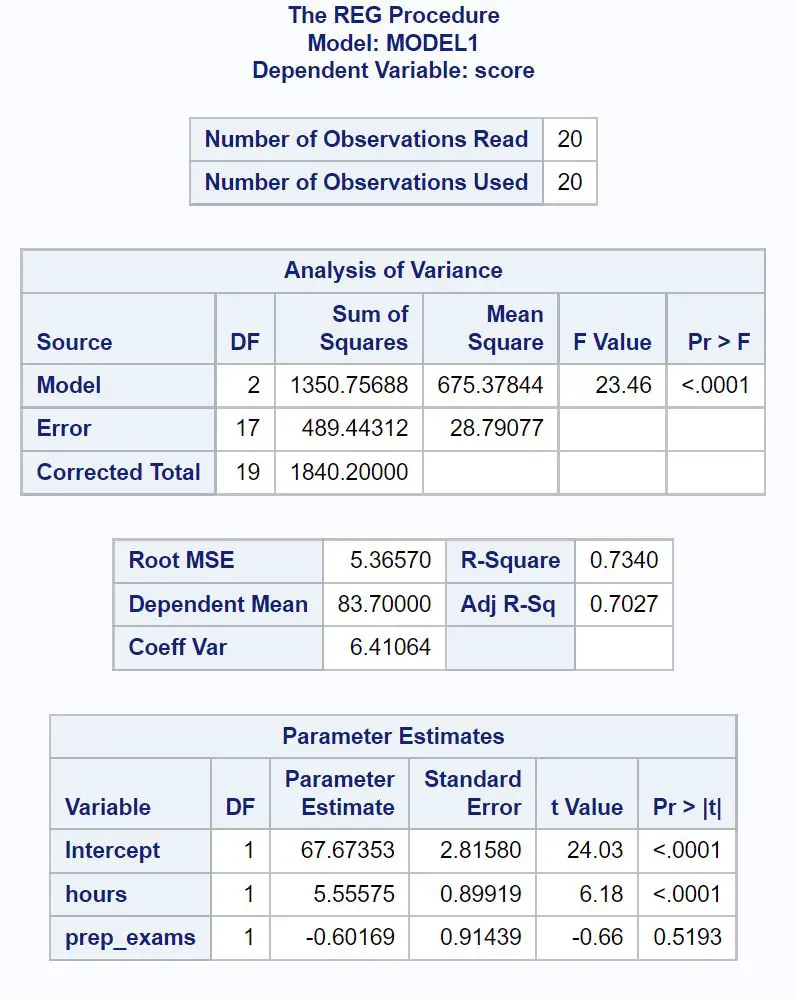
Voici comment interpréter les nombres les plus pertinents de chaque tableau :
Tableau d’analyse des écarts :
La valeur F globale du modèle de régression est de 23,46 et la valeur p correspondante est <0,0001 .
Puisque cette valeur p est inférieure à 0,05, nous concluons que le modèle de régression dans son ensemble est statistiquement significatif.
Tableau d’ajustement du modèle :
La valeur R-Carré nous indique le pourcentage de variation des résultats des examens qui peut s’expliquer par le nombre d’heures étudiées et le nombre d’examens préparatoires passés.
En général, plus la valeur R au carré d’un modèle de régression est grande, plus les variables prédictives sont capables de prédire la valeur de la variable de réponse.
Dans ce cas, 73,4 % de la variation des résultats aux examens peut s’expliquer par le nombre d’heures étudiées et le nombre d’examens préparatoires passés.
La valeur Root MSE est également utile à connaître. Cela représente la distance moyenne entre les valeurs observées et la droite de régression.
Dans ce modèle de régression, les valeurs observées s’éloignent en moyenne de 5,3657 unités de la droite de régression.
Tableau des estimations des paramètres :
Nous pouvons utiliser les valeurs d’estimation des paramètres dans ce tableau pour écrire l’équation de régression ajustée :
Score d’examen = 67,674 + 5,556*(heures) – 0,602*(prep_exams)
Nous pouvons utiliser cette équation pour trouver la note estimée à l’examen d’un étudiant, en fonction du nombre d’heures d’études et du nombre d’examens préparatoires qu’il a passés.
Par exemple, un étudiant qui étudie pendant 3 heures et passe 2 examens préparatoires devrait recevoir une note à l’examen de 83,1 :
Note estimée à l’examen = 67,674 + 5,556*(3) – 0,602*(2) = 83,1
La valeur p pour les heures (<0,0001) est inférieure à 0,05, ce qui signifie qu’elle a une association statistiquement significative avec le résultat de l’examen.
Cependant, la valeur p pour les examens préparatoires (0,5193) n’est pas inférieure à 0,05, ce qui signifie qu’elle n’a pas d’association statistiquement significative avec le résultat de l’examen.
Nous pouvons décider de supprimer les examens préparatoires du modèle, car ils ne sont pas statistiquement significatifs, et d’effectuer à la place une simple régression linéaire en utilisant les heures étudiées comme seule variable prédictive.
Ressources additionnelles
Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes dans SAS :
Comment calculer la corrélation dans SAS
Comment effectuer une régression linéaire simple dans SAS
Comment effectuer une ANOVA unidirectionnelle dans SAS
