Comment effectuer une régression linéaire multiple dans Excel

La régression linéaire multiple est une méthode que nous pouvons utiliser pour comprendre la relation entre deux ou plusieurs variables explicatives et une variable de réponse .

Ce didacticiel explique comment effectuer une régression linéaire multiple dans Excel.

Remarque : Si vous n’avez qu’une seule variable explicative, vous devez plutôt effectuer une régression linéaire simple .

Exemple : régression linéaire multiple dans Excel

Supposons que nous voulions savoir si le nombre d’heures passées à étudier et le nombre d’examens préparatoires passés affectent la note qu’un étudiant obtient à un certain examen d’entrée à l’université.

Pour explorer cette relation, nous pouvons effectuer une régression linéaire multiple en utilisant les heures étudiées et les examens préparatoires passés comme variables explicatives et les résultats de l’examen comme variable de réponse.

Effectuez les étapes suivantes dans Excel pour effectuer une régression linéaire multiple.

Étape 1 : Saisissez les données.

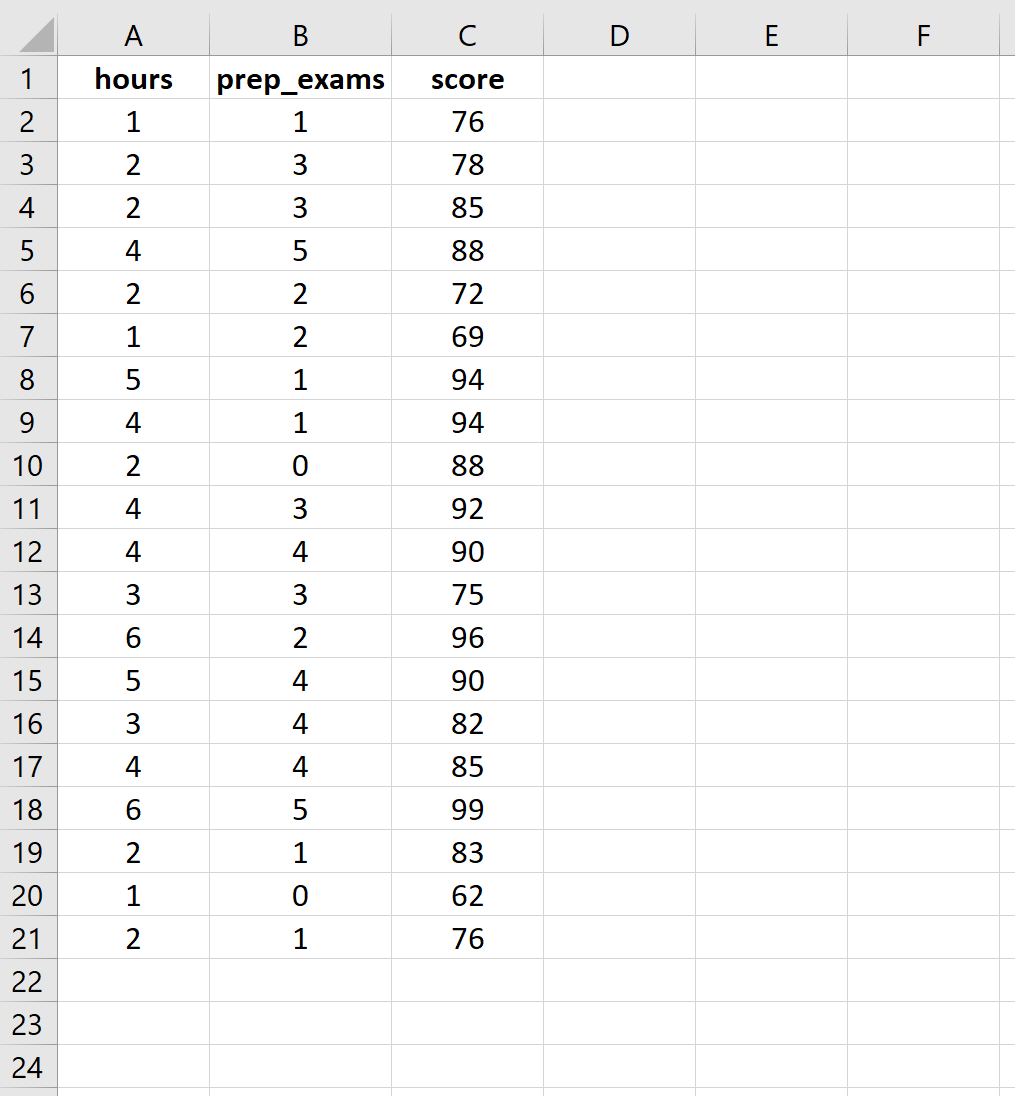
Saisissez les données suivantes pour le nombre d’heures étudiées, les examens préparatoires passés et les résultats des examens reçus pour 20 étudiants :

Étape 2 : Effectuez une régression linéaire multiple.

Dans le ruban supérieur d’Excel, accédez à l’onglet Données et cliquez sur Analyse des données . Si vous ne voyez pas cette option, vous devez d’abord installer le logiciel gratuit Analysis ToolPak .

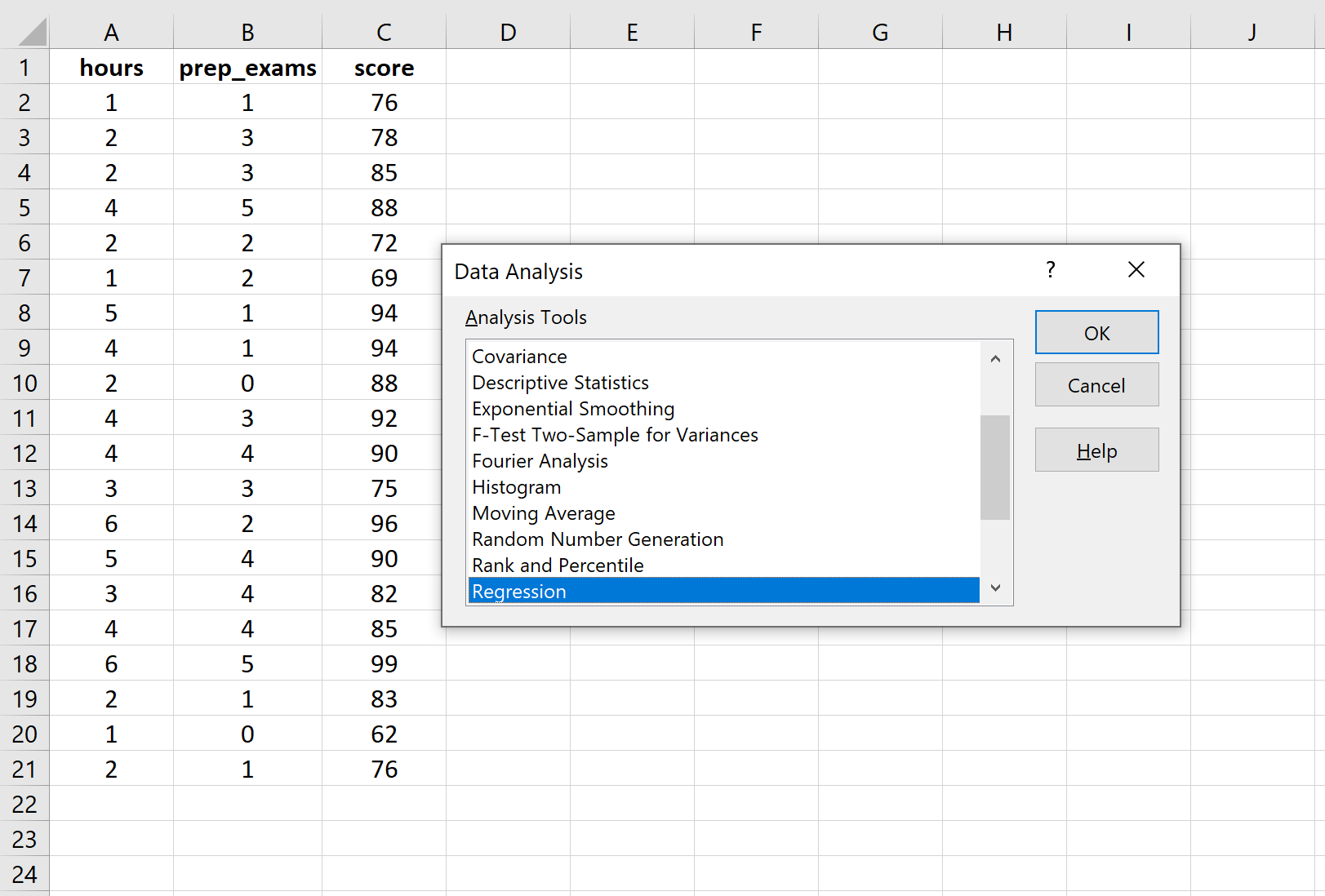
Une fois que vous avez cliqué sur Analyse des données, une nouvelle fenêtre apparaîtra. Sélectionnez Régression et cliquez sur OK.

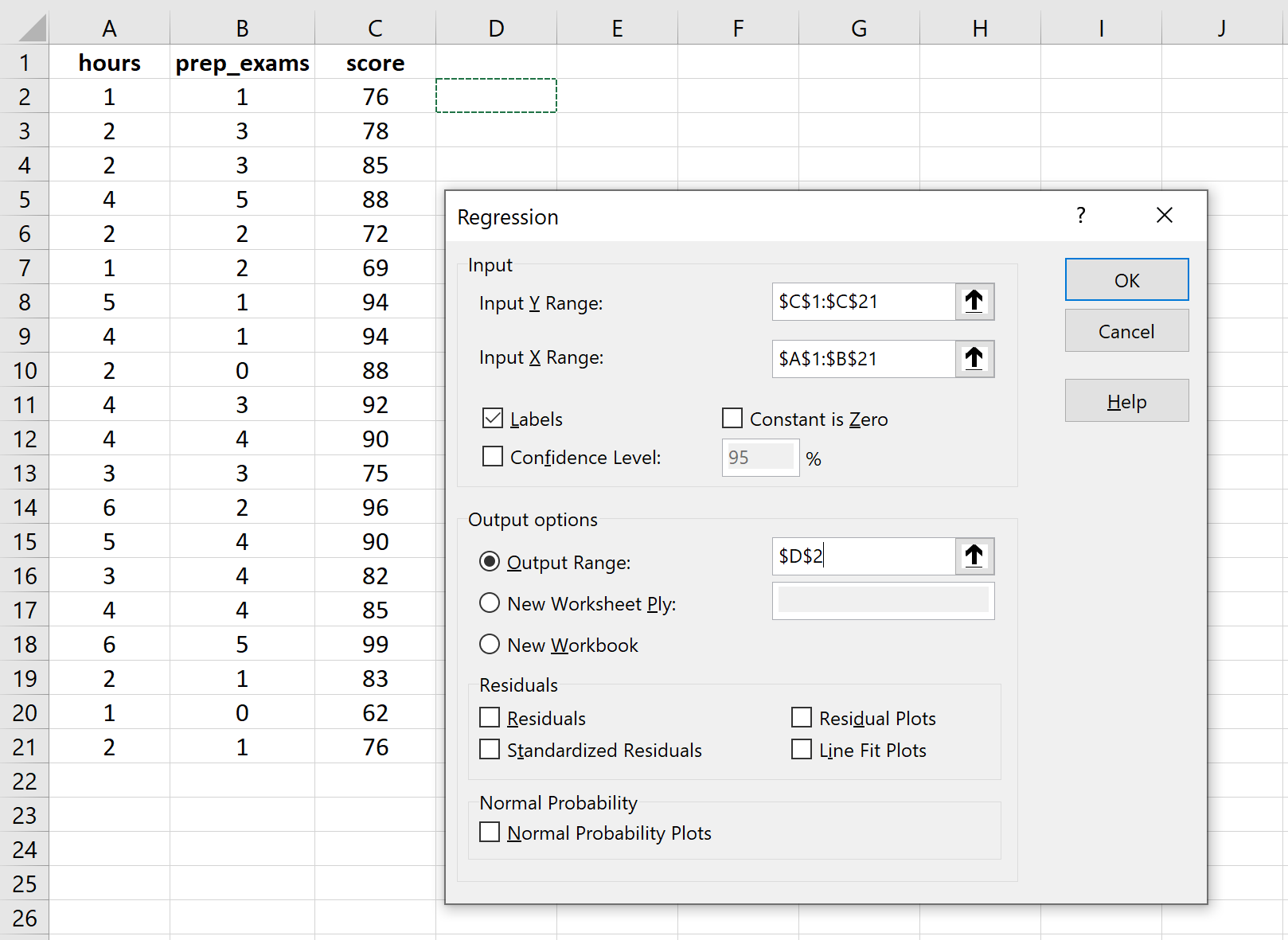
Pour Input Y Range , remplissez le tableau de valeurs pour la variable de réponse. Pour Input X Range , remplissez le tableau de valeurs pour les deux variables explicatives. Cochez la case à côté de Étiquettes pour qu’Excel sache que nous avons inclus les noms de variables dans les plages d’entrée. Pour Plage de sortie , sélectionnez une cellule dans laquelle vous souhaitez que la sortie de la régression apparaisse. Cliquez ensuite sur OK .

La sortie suivante apparaîtra automatiquement :

Étape 3 : Interprétez le résultat.

Voici comment interpréter les nombres les plus pertinents dans le résultat :

R Carré : 0,734 . C’est ce qu’on appelle le coefficient de détermination. C’est la proportion de la variance de la variable de réponse qui peut être expliquée par les variables explicatives. Dans cet exemple, 73,4 % de la variation des résultats aux examens s’explique par le nombre d’heures étudiées et le nombre d’examens préparatoires passés.

Erreur type : 5,366 . Il s’agit de la distance moyenne entre les valeurs observées et la droite de régression. Dans cet exemple, les valeurs observées s’éloignent en moyenne de 5,366 unités de la droite de régression.

F : 23h46 . Il s’agit de la statistique F globale pour le modèle de régression, calculée comme MS de régression / MS résiduelle.

Signification F : 0,0000 . Il s’agit de la valeur p associée à la statistique F globale. Cela nous indique si le modèle de régression dans son ensemble est statistiquement significatif ou non. En d’autres termes, cela nous indique si les deux variables explicatives combinées ont une association statistiquement significative avec la variable de réponse. Dans ce cas, la valeur p est inférieure à 0,05, ce qui indique que les variables explicatives , les heures étudiées et les examens préparatoires passés combinés, ont une association statistiquement significative avec le résultat de l’examen .

Valeurs P. Les valeurs p individuelles nous indiquent si chaque variable explicative est statistiquement significative ou non. Nous pouvons voir que les heures étudiées sont statistiquement significatives (p = 0,00) tandis que les examens préparatoires passés (p = 0,52) ne sont pas statistiquement significatifs à α = 0,05. Étant donné que les examens préparatoires passés ne sont pas statistiquement significatifs, nous pourrions finir par décider de les supprimer du modèle.

Coefficients : Les coefficients de chaque variable explicative nous indiquent le changement moyen attendu de la variable de réponse, en supposant que l’autre variable explicative reste constante. Par exemple, pour chaque heure supplémentaire consacrée à étudier, la note moyenne à l’examen devrait augmenter de 5,56 , en supposant que les examens préparatoires passés restent constants.

Voici une autre façon de voir les choses : si l’étudiant A et l’étudiant B passent tous deux le même nombre d’examens préparatoires mais que l’étudiant A étudie une heure de plus, alors l’étudiant A devrait obtenir un score supérieur de 5,56 points à celui de l’étudiant B.

Nous interprétons le coefficient de l’interception comme signifiant que la note attendue à l’examen pour un étudiant qui n’étudie aucune heure et ne passe aucun examen préparatoire est de 67,67 .

Équation de régression estimée : nous pouvons utiliser les coefficients de la sortie du modèle pour créer l’équation de régression estimée suivante :

score à l’examen = 67,67 + 5,56*(heures) – 0,60*(examens préparatoires)

Nous pouvons utiliser cette équation de régression estimée pour calculer la note attendue à l’examen pour un étudiant, en fonction du nombre d’heures d’études et du nombre d’examens préparatoires qu’il passe. Par exemple, un étudiant qui étudie pendant trois heures et passe un examen préparatoire devrait obtenir une note de 83,75 :

note à l’examen = 67,67 + 5,56*(3) – 0,60*(1) = 83,75

Gardez à l’esprit que, comme les examens préparatoires passés n’étaient pas statistiquement significatifs (p = 0,52), nous pouvons décider de les supprimer car ils n’apportent aucune amélioration au modèle global. Dans ce cas, nous pourrions effectuer une régression linéaire simple en utilisant uniquement les heures étudiées comme variable explicative.

Les résultats de cette simple analyse de régression linéaire peuvent être trouvés ici .

Ressources additionnelles

Une fois que vous avez effectué une régression linéaire multiple, vous souhaiterez peut-être vérifier plusieurs hypothèses, notamment :

1. Test de multicolinéarité à l’aide de VIF .

2. Test d’hétérodscédasticité à l’aide d’un test de Breusch-Pagan .

3. Test de normalité à l’aide d’un tracé QQ .