Comment effectuer une régression linéaire multiple dans SPSS

La régression linéaire multiple est une méthode que nous pouvons utiliser pour comprendre la relation entre deux ou plusieurs variables explicatives et une variable de réponse.

Ce didacticiel explique comment effectuer une régression linéaire multiple dans SPSS.

Exemple : régression linéaire multiple dans SPSS

Supposons que nous voulions savoir si le nombre d’heures passées à étudier et le nombre d’examens préparatoires passés affectent la note qu’un étudiant obtient à un examen donné. Pour explorer cela, nous pouvons effectuer une régression linéaire multiple en utilisant les variables suivantes :

Variables explicatives:

• Heures étudiées
• Examens préparatoires passés

Variable de réponse:

• Résultat de l’examen

Utilisez les étapes suivantes pour effectuer cette régression linéaire multiple dans SPSS.

Étape 1 : Saisissez les données.

Saisissez les données suivantes pour le nombre d’heures étudiées, les examens préparatoires passés et les résultats des examens reçus pour 20 étudiants :

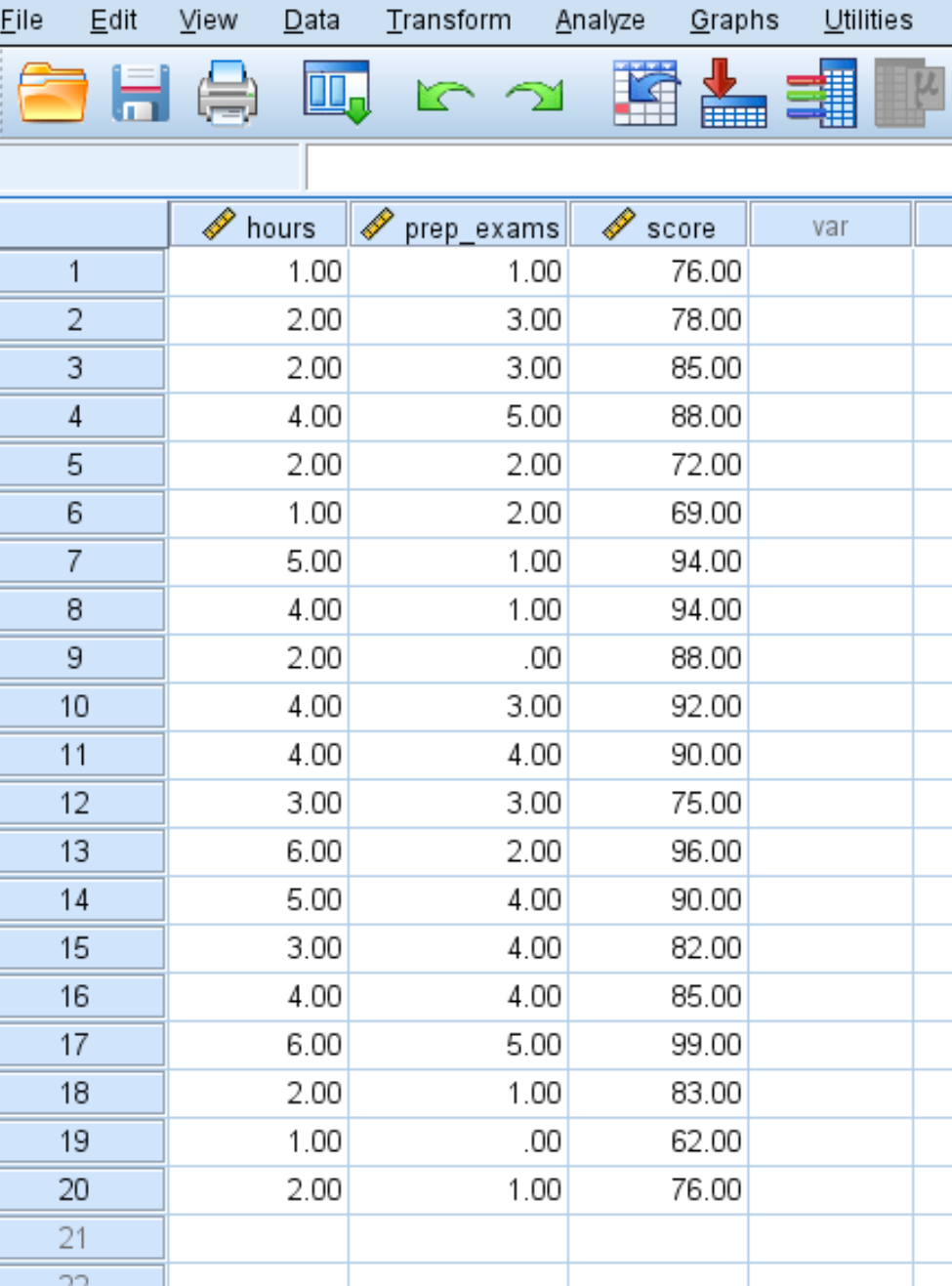
Étape 2 : Effectuez une régression linéaire multiple.

Cliquez sur l’onglet Analyser , puis Régression , puis Linéaire :

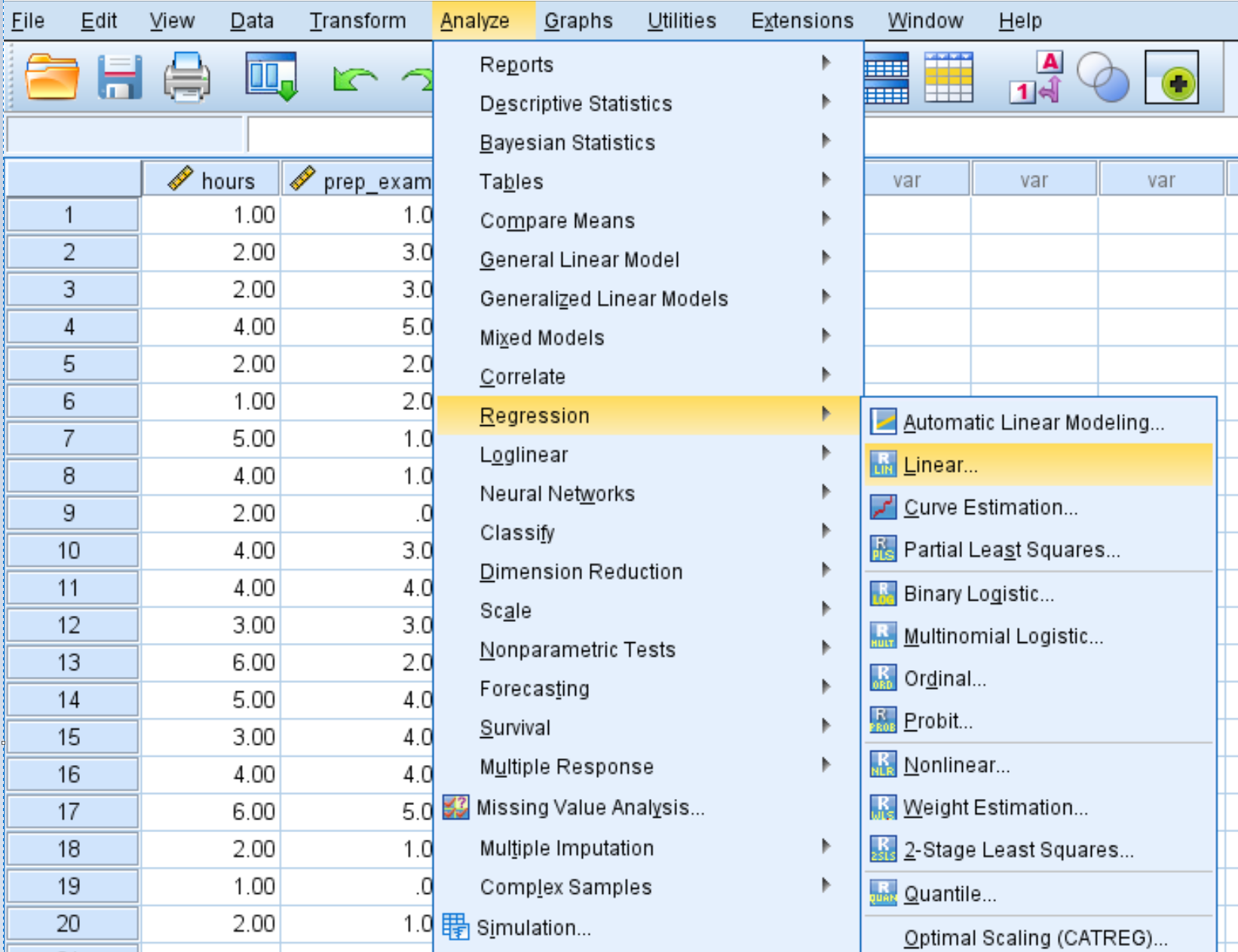
Faites glisser le score variable dans la case intitulée Dépendant. Faites glisser les variables hours et prep_exams dans la zone intitulée Independent(s). Cliquez ensuite sur OK .

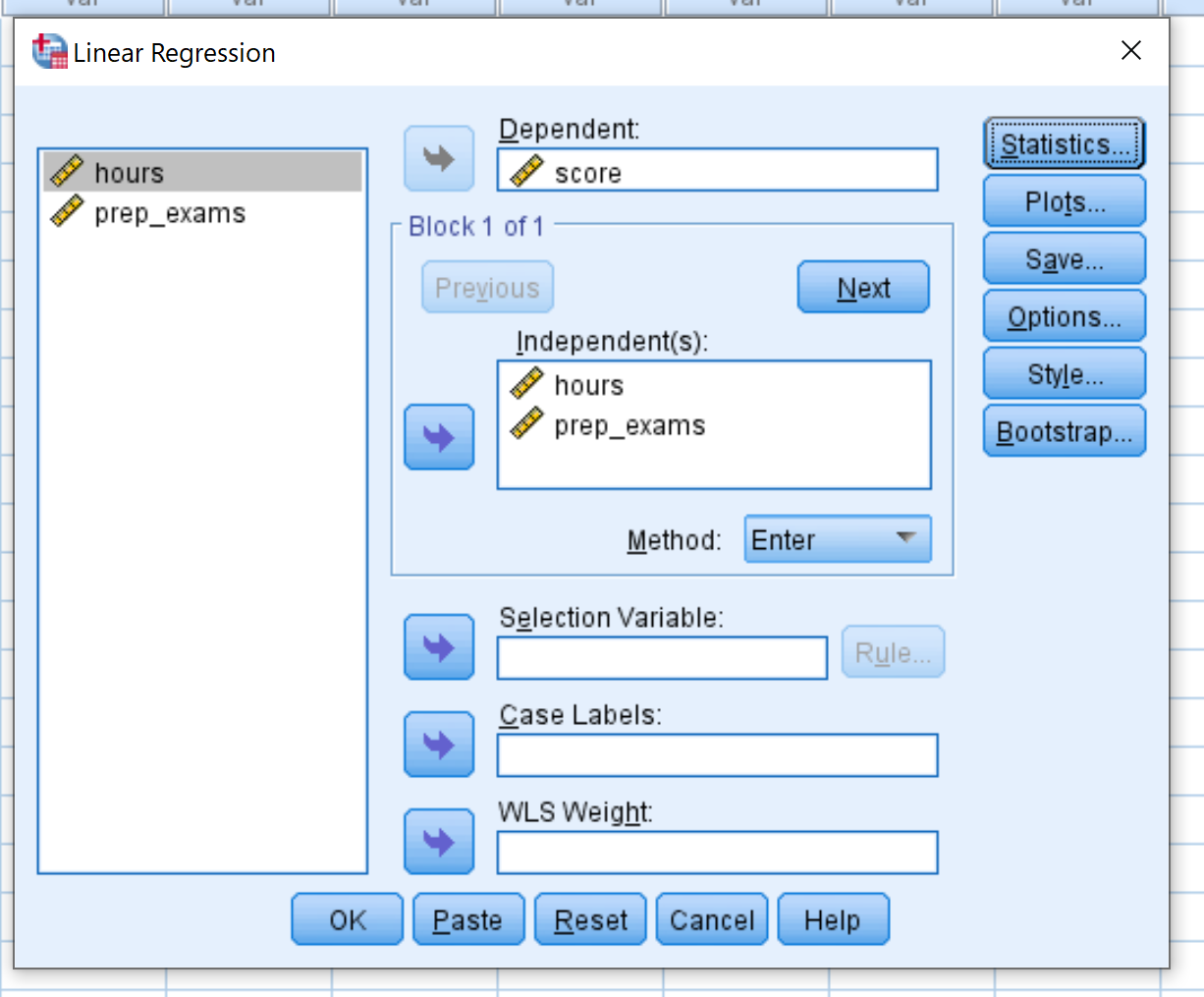
Étape 3 : Interprétez le résultat.

Une fois que vous avez cliqué sur OK , les résultats de la régression linéaire multiple apparaîtront dans une nouvelle fenêtre.

Le premier tableau qui nous intéresse s’intitule Model Summary :

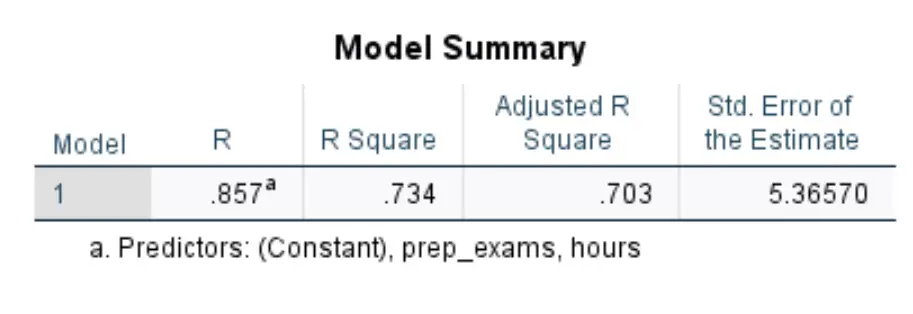
Voici comment interpréter les chiffres les plus pertinents de ce tableau :

• R Carré : Il s’agit de la proportion de la variance de la variable de réponse qui peut être expliquée par les variables explicatives. Dans cet exemple, 73,4 % de la variation des résultats aux examens peut s’expliquer par les heures étudiées et le nombre d’examens préparatoires passés.
• Norme. Erreur d’estimation : l’ erreur type est la distance moyenne entre les valeurs observées et la droite de régression. Dans cet exemple, les valeurs observées s’éloignent en moyenne de 5,3657 unités de la droite de régression.

Le tableau suivant qui nous intéresse s’intitule ANOVA :

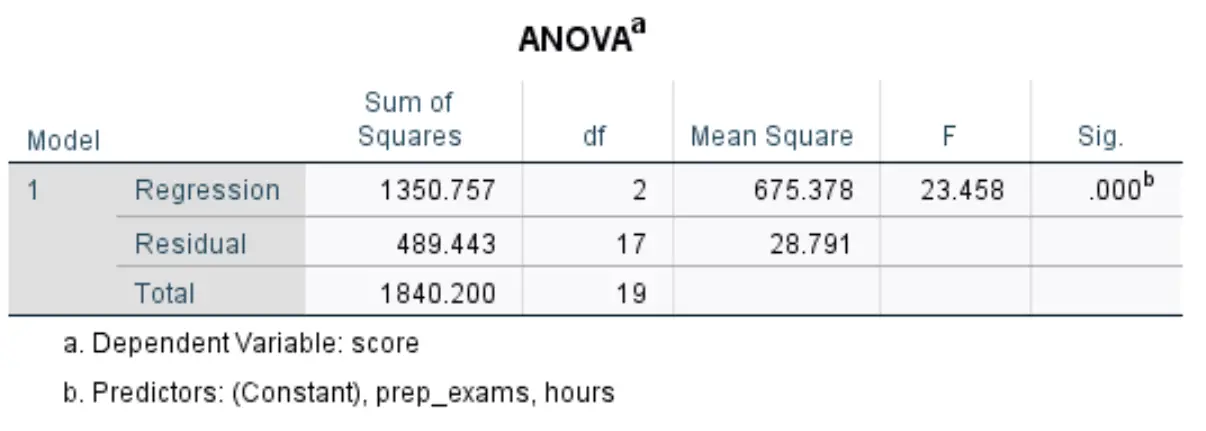
Voici comment interpréter les chiffres les plus pertinents de ce tableau :

• F : Il s’agit de la statistique F globale pour le modèle de régression, calculée comme Régression quadratique moyenne / Résidu quadratique moyen.
• Sig : Il s’agit de la valeur p associée à la statistique F globale. Cela nous indique si le modèle de régression dans son ensemble est statistiquement significatif ou non. En d’autres termes, cela nous indique si les deux variables explicatives combinées ont une association statistiquement significative avec la variable de réponse. Dans ce cas, la valeur p est égale à 0,000, ce qui indique que les variables explicatives, les heures étudiées et les examens préparatoires passés, ont une association statistiquement significative avec le résultat de l’examen.

Le tableau suivant qui nous intéresse s’intitule Coefficients :

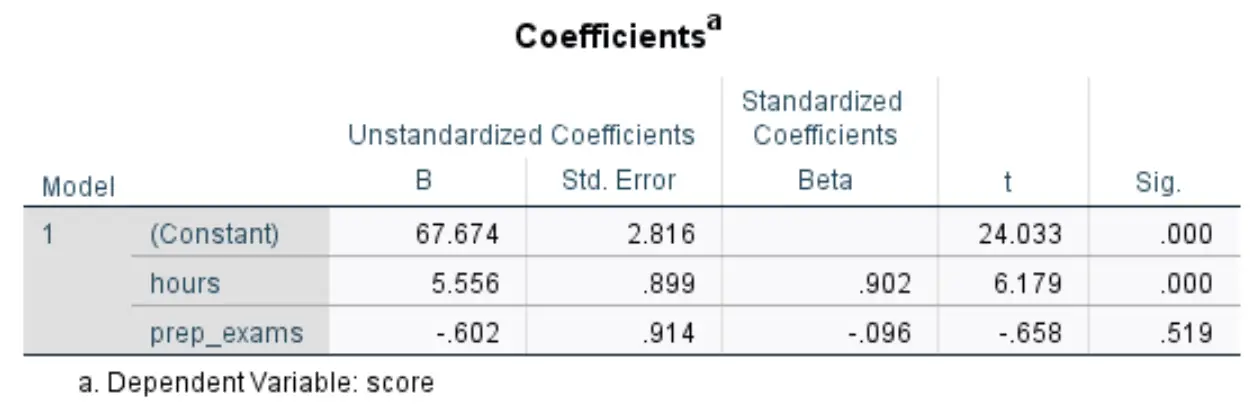
Voici comment interpréter les chiffres les plus pertinents de ce tableau :

• B non standardisé (constante) : cela nous indique la valeur moyenne de la variable de réponse lorsque les deux variables prédictives sont nulles. Dans cet exemple, la note moyenne à l’examen est de 67,674 lorsque les heures étudiées et les examens préparatoires passés sont tous deux égaux à zéro.
• B non standardisé (heures) : cela nous indique la variation moyenne des résultats à l’examen associée à une augmentation d’une unité des heures d’études, en supposant que le nombre d’examens préparatoires passés reste constant. Dans ce cas, chaque heure supplémentaire passée à étudier est associée à une augmentation de 5,556 points de la note à l’examen, en supposant que le nombre d’examens préparatoires passés reste constant.
• Non standardisé B (prep_exams) : cela nous indique la variation moyenne de la note à l’examen associée à une augmentation d’une unité des examens préparatoires passés, en supposant que le nombre d’heures étudiées reste constant. Dans ce cas, chaque examen préparatoire supplémentaire passé est associé à une diminution de 0,602 points de la note à l’examen, en supposant que le nombre d’heures étudiées reste constant.
• Sig. (heures) : Il s’agit de la valeur p pour la variable explicative heures . Puisque cette valeur (0,000) est inférieure à 0,05, nous pouvons conclure que les heures étudiées ont une association statistiquement significative avec les résultats à l’examen.
• Sig. (prep_exams) : il s’agit de la valeur p pour la variable explicative prep_exams . Étant donné que cette valeur (0,519) n’est pas inférieure à 0,05, nous ne pouvons pas conclure que le nombre d’examens préparatoires passés a une association statistiquement significative avec le résultat de l’examen.

Enfin, nous pouvons former une équation de régression en utilisant les valeurs indiquées dans le tableau pour constant , hours et prep_exams . Dans ce cas, l’équation serait :

Note estimée à l’examen = 67,674 + 5,556*(heures) – 0,602*(prep_exams)

Nous pouvons utiliser cette équation pour trouver la note estimée à l’examen d’un étudiant, en fonction du nombre d’heures d’études et du nombre d’examens préparatoires qu’il a passés. Par exemple, un étudiant qui étudie pendant 3 heures et passe 2 examens préparatoires devrait recevoir une note d’examen de 83,1 :

Note estimée à l’examen = 67,674 + 5,556*(3) – 0,602*(2) = 83,1

Remarque : Étant donné que la variable explicative des examens préparatoires ne s’est pas révélée statistiquement significative, nous pouvons décider de la supprimer du modèle et d’effectuer à la place une régression linéaire simple en utilisant les heures étudiées comme seule variable explicative.