Régression linéaire simple

Par Pr Amélia Rodriguez août 2, 2023 Statistiques 0 commentaire

Cet article explique ce qu’est la régression linéaire simple en statistique et comment elle est réalisée. De même, vous trouverez un exercice de régression linéaire simple résolu et, en plus, un calculateur de régression linéaire simple en ligne.

Qu’est-ce que la régression linéaire simple ?

La régression linéaire simple est un modèle statistique utilisé pour relier une variable indépendante X à une variable dépendante Y. Autrement dit, dans une régression linéaire simple, il n’y a que deux variables (la variable explicative X et la variable de réponse Y) et on tente de approximer la relation Qu’est-ce qu’il y a entre les deux variables.

Par conséquent, une régression linéaire simple est utilisée pour trouver une équation qui relie deux variables de manière linéaire. Logiquement, la relation entre les deux variables doit être linéaire, sinon un autre type de modèle de régression doit être utilisé.

L’équation d’un modèle de régression linéaire simple est composée de deux coefficients : la constante de l’équation (b ₀ ) et le coefficient de corrélation entre les deux variables (b ₁ ). Par conséquent, l’équation d’un modèle de régression linéaire simple est y=b ₀ +b ₁ x.

$y=b_0+b_1x$

L’équation d’une régression linéaire simple est représentée graphiquement par une ligne droite, donc le coefficient b ₀ est l’ordonnée à l’origine et le coefficient b ₁ est la pente de la ligne.

Formules de régression linéaire simples

Les formules pour calculer les coefficients d’une régression linéaire simple sont les suivantes :

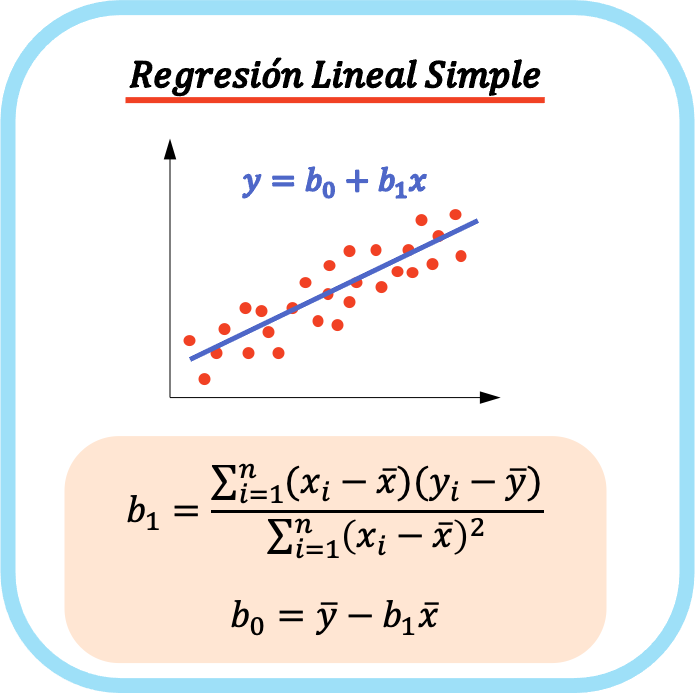
👉 Vous pouvez utiliser la calculatrice ci-dessous pour calculer les coefficients d’une régression linéaire simple pour n’importe quel ensemble de données.

Évidemment, l’équation résultant du modèle de régression linéaire simple ne pourra pas deviner la valeur exacte de toutes les observations, puisque ce modèle tente simplement de trouver une équation qui se rapproche de la relation entre les deux variables. Ainsi, le résidu est défini comme la différence entre la valeur réelle et la valeur estimée par le modèle de régression linéaire.

$e_i=y_i-\widehat{y}_i$

Notez que l’objectif d’un modèle de régression linéaire simple est de minimiser les carrés des résidus, c’est-à-dire que la régression linéaire simple est basée sur le critère des moindres carrés .

Exemple concret d’une régression linéaire simple

Pour finir de comprendre la méthode de régression linéaire simple, voici un exemple concret étape par étape dans lequel l’équation d’un modèle de régression linéaire simple est calculée à partir d’un ensemble de données statistiques.

Après avoir passé un examen de statistiques, il a été demandé à cinq étudiants combien d’heures d’études ils avaient consacré à l’examen. Les données sont présentées dans le tableau ci-dessous. Effectuez un modèle de régression linéaire simple des données statistiques collectées pour relier linéairement les heures d’études à la note obtenue.

Pour réaliser un modèle de régression linéaire simple, nous devons déterminer les coefficients b ₀ et b ₁ de l’équation et, pour cela, nous devons utiliser les formules vues dans la section ci-dessus.

Cependant, pour appliquer les formules simples de régression linéaire, nous devons d’abord calculer la moyenne de la variable indépendante et la moyenne de la variable dépendante :

$\begin{array}{c}\overline{x}=\cfrac{11+5+10+12+7}{5}=9\\[4ex]\overline{y}=\cfrac{7+4+5+8+6}{5}=6\end{array}$

Maintenant que l’on connaît les moyennes des variables, on calcule le coefficient b ₁ du modèle à l’aide de sa formule correspondante :

$\begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[10ex] b_1=\cfrac{\begin{array}{c}(11-9)(7-6)+(5-9)(4-6)+(10-9)(5-6)+\\+(12-9)(8-6)+(7-9)(6-6)\end{array}}{(11-9)^2+(5-9)^2+(10-9)^2+(12-9)^2+(7-9)^2}\\[6ex]b_1=0,4412\end{array}$

Enfin, on calcule le coefficient b ₀ du modèle à l’aide de sa formule correspondante :

$\begin{array}{l}b_0=\overline{y}-b_1\overline{x}\\[3ex]b_0=6-0,4412\cdot 9 \\[3ex]b_0=2,0294\end{array}$

En bref, l’équation du modèle de régression linéaire simple du problème est la suivante :

$y=2,0294+0,4412x$

Ci-dessous, vous pouvez voir la représentation graphique de l’échantillon de données ainsi que la ligne droite du modèle de régression linéaire simple :

Enfin, une fois que l’on a calculé l’équation du modèle de régression linéaire simple, il ne reste plus qu’à interpréter le résultat obtenu. Pour cela, il est indispensable de calculer le coefficient de détermination du modèle de régression, vous pouvez voir comment cela se fait en recherchant l’article correspondant sur notre site internet.

Hypothèses de régression linéaire simple

Afin d’effectuer une régression linéaire simple, les hypothèses suivantes doivent être respectées :

Indépendance : les résidus observés doivent être indépendants les uns des autres. Une manière courante de garantir l’indépendance du modèle consiste à ajouter du caractère aléatoire au processus d’échantillonnage.
Homoscédasticité : il doit y avoir une homogénéité dans les variances des résidus, c’est-à-dire que la variabilité des résidus doit être constante.
Normalité : les résidus doivent être distribués normalement, ou en d’autres termes, ils doivent suivre une distribution normale de moyenne 0.
Linéarité – La relation entre la variable indépendante et la variable dépendante doit être linéaire.

Calculateur de régression linéaire simple

Branchez un échantillon de données dans la calculatrice ci-dessous pour ajuster un modèle de régression linéaire simple entre deux variables. Vous devez séparer les paires de données, de sorte que dans la première case il n’y ait que les valeurs de la variable indépendante X et dans la deuxième case il n’y ait que les valeurs de la variable dépendante Y.

Les données doivent être séparées par un espace et saisies en utilisant le point comme séparateur décimal.

Régression linéaire simple et multiple

Enfin, nous verrons quelle est la différence entre la régression linéaire simple et la régression linéaire multiple, puisque ce sont deux types de régressions linéaires fréquemment utilisées en statistique.

La régression linéaire multiple permet de relier mathématiquement deux ou plusieurs variables explicatives à une variable de réponse. Autrement dit, dans la régression linéaire multiple, un modèle est créé dans lequel il existe au moins deux variables indépendantes.

Par conséquent, la différence entre la régression linéaire simple et la régression linéaire multiple réside dans le nombre de variables indépendantes. Dans la régression linéaire simple, il n’y a qu’une seule variable indépendante, tandis que dans la régression linéaire multiple, il y a deux variables indépendantes ou plus.

➤ Voir : Régression linéaire multiple

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus