Comment effectuer une régression logistique dans SAS

La régression logistique est une méthode que nous pouvons utiliser pour ajuster un modèle de régression lorsque la variable de réponse est binaire.

La régression logistique utilise une méthode connue sous le nom d’estimation du maximum de vraisemblance pour trouver une équation de la forme suivante :

log[p(X) / (1-p(X))] = β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p X _p

où:

• X _j : la j ^ème variable prédictive
• β _j : estimation du coefficient pour la j ^ème variable prédictive

La formule sur le côté droit de l’équation prédit le log des chances que la variable de réponse prenne la valeur 1.

L’exemple étape par étape suivant montre comment ajuster un modèle de régression logistique dans SAS.

Étape 1 : Créer l’ensemble de données

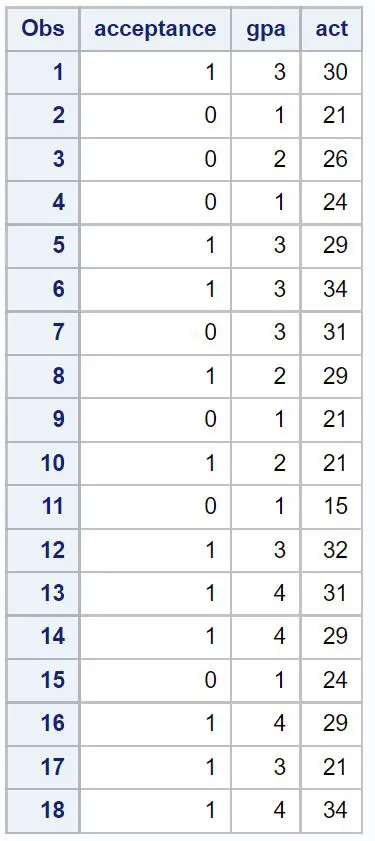
Tout d’abord, nous allons créer un ensemble de données contenant des informations sur les trois variables suivantes pour 18 étudiants :

• Acceptation dans un certain collège (1 = oui, 0 = non)
• GPA (échelle de 1 à 4)
• Score ACT (échelle de 1 à 36)

/*create dataset*/
data my_data;
    input acceptance gpa act;
    datalines;
1 3 30
0 1 21
0 2 26
0 1 24
1 3 29
1 3 34
0 3 31
1 2 29
0 1 21
1 2 21
0 1 15
1 3 32
1 4 31
1 4 29
0 1 24
1 4 29
1 3 21
1 4 34
;
run;

/*view dataset*/
proc print data=my_data;

Étape 2 : Ajuster le modèle de régression logistique

Ensuite, nous utiliserons la logistique proc pour ajuster le modèle de régression logistique, en utilisant « acceptation » comme variable de réponse et « gpa » et « agir » comme variables prédictives.

Remarque : Il faut spécifier décroissant pour que SAS sache prédire la probabilité que la variable de réponse prenne une valeur de 1. Par défaut, SAS prédit la probabilité que la variable de réponse prenne une valeur de 0.

/*fit logistic regression model*/
proc logistic data=my_data descending;
  model acceptance = gpa act;
run;

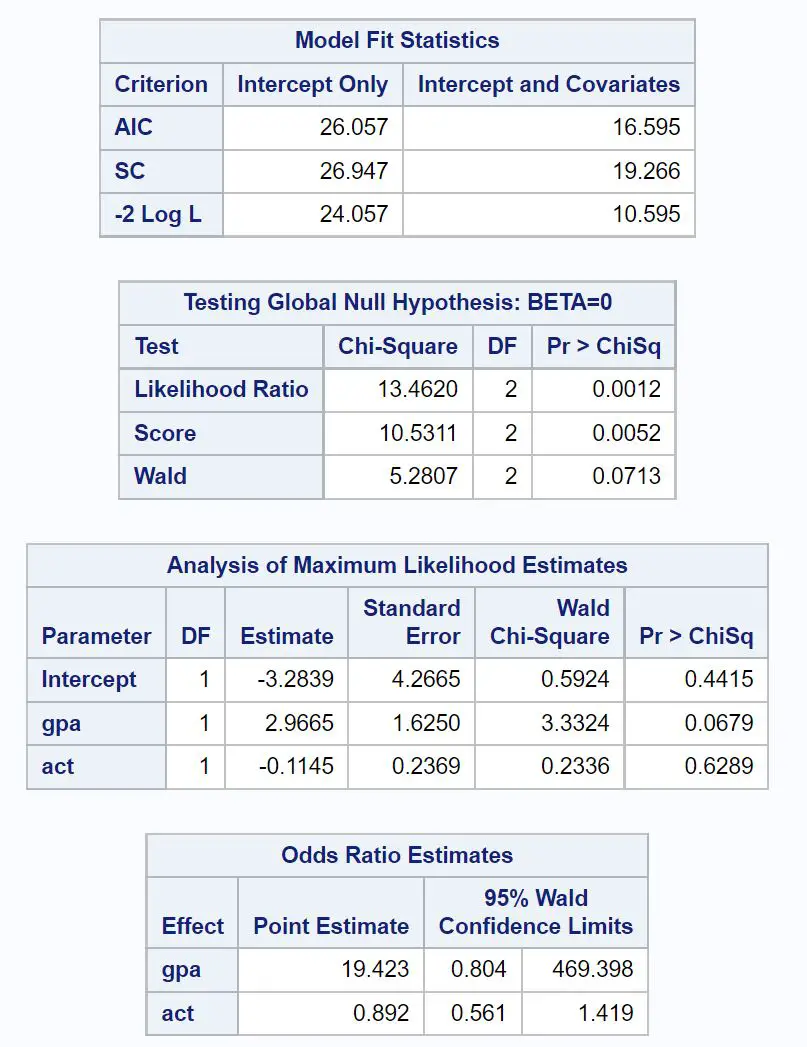
Le premier tableau intéressant est intitulé Model Fit Statistics .

À partir de ce tableau, nous pouvons voir la valeur AIC du modèle, qui s’avère être de 16,595 . Plus la valeur AIC est faible, plus le modèle est capable de s’adapter aux données.

Cependant, il n’y a pas de seuil pour ce qui est considéré comme une « bonne » valeur AIC . Nous utilisons plutôt l’AIC pour comparer l’ajustement de plusieurs modèles au même ensemble de données. Le modèle avec la valeur AIC la plus basse est généralement considéré comme le meilleur.

Le prochain tableau intéressant est intitulé Test de l’hypothèse nulle globale : BETA=0 .

À partir de ce tableau, nous pouvons voir la valeur du chi carré du rapport de vraisemblance de 13,4620 avec une valeur p correspondante de 0,0012 .

Puisque cette valeur p est inférieure à 0,05, cela nous indique que le modèle de régression logistique dans son ensemble est statistiquement significatif.

Ensuite, nous pouvons analyser les estimations des coefficients dans le tableau intitulé Analyse des estimations du maximum de vraisemblance .

À partir de ce tableau, nous pouvons voir les coefficients pour gpa et act, qui indiquent la variation moyenne du log des chances d’être accepté à l’université pour une augmentation d’une unité dans chaque variable.

Par exemple:

• Une augmentation d’une unité de la valeur GPA est associée à une augmentation moyenne de 2,9665 du log des chances d’être accepté à l’université.
• Une augmentation d’une unité du score ACT est associée à une diminution moyenne de 0,1145 du log des chances d’être accepté à l’université.

Les valeurs p correspondantes dans le résultat nous donnent également une idée de l’efficacité de chaque variable prédictive pour prédire la probabilité d’être accepté :

• Valeur P du GPA : 0,0679
• Valeur P de l’ACT : 0,6289

Cela nous indique que la GPA semble être un prédicteur statistiquement significatif de l’acceptation à l’université, tandis que le score ACT ne semble pas être statistiquement significatif.

Ressources additionnelles

Les didacticiels suivants expliquent comment adapter d’autres modèles de régression dans SAS :

Comment effectuer une régression linéaire simple dans SAS
Comment effectuer une régression linéaire multiple dans SAS