Comment effectuer une régression logistique en Python (étape par étape)

La régression logistique est une méthode que nous pouvons utiliser pour ajuster un modèle de régression lorsque la variable de réponse est binaire.

La régression logistique utilise une méthode connue sous le nom d’estimation du maximum de vraisemblance pour trouver une équation de la forme suivante :

log[p(X) / (1-p(X))] = β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p X _p

où:

• X _j : la j ^ème variable prédictive
• β _j : estimation du coefficient pour la j ^ème variable prédictive

La formule sur le côté droit de l’équation prédit le log des chances que la variable de réponse prenne la valeur 1.

Ainsi, lorsque nous ajustons un modèle de régression logistique, nous pouvons utiliser l’équation suivante pour calculer la probabilité qu’une observation donnée prenne la valeur 1 :

p(X) = e ^{β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p X _p} / (1 + e ^{β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p X _p} )

Nous utilisons ensuite un certain seuil de probabilité pour classer l’observation comme 1 ou 0.

Par exemple, nous pourrions dire que les observations avec une probabilité supérieure ou égale à 0,5 seront classées comme « 1 » et que toutes les autres observations seront classées comme « 0 ».

Ce didacticiel fournit un exemple étape par étape de la façon d’effectuer une régression logistique dans R.

Étape 1 : Importer les packages nécessaires

Tout d’abord, nous allons importer les packages nécessaires pour effectuer une régression logistique en Python :

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn import metrics
import matplotlib.pyplot as plt

Étape 2 : Charger les données

Pour cet exemple, nous utiliserons l’ensemble de données par défaut du livre Introduction à l’apprentissage statistique . Nous pouvons utiliser le code suivant pour charger et afficher un résumé de l’ensemble de données :

#import dataset from CSV file on Github
url = "https://raw.githubusercontent.com/Statology/Python-Guides/main/default.csv"
data = pd.read_csv(url)

#view first six rows of dataset
data[0:6]

        default	student	balance	        income
0	0	0	729.526495	44361.625074
1	0	1	817.180407	12106.134700
2	0	0	1073.549164	31767.138947
3	0	0	529.250605	35704.493935
4	0	0	785.655883	38463.495879
5	0	1	919.588530	7491.558572  

#find total observations in dataset
len(data.index)

10000

Cet ensemble de données contient les informations suivantes sur 10 000 individus :

• défaut : indique si un individu a fait défaut ou non.
• étudiant : indique si un individu est étudiant ou non.
• solde : Solde moyen porté par un individu.
• revenu : Revenu de l’individu.

Nous utiliserons le statut d’étudiant, le solde bancaire et le revenu pour construire un modèle de régression logistique qui prédit la probabilité qu’un individu donné fasse défaut.

Étape 3 : Créer des échantillons de formation et de test

Ensuite, nous diviserons l’ensemble de données en un ensemble d’entraînement sur lequel entraîner le modèle et un ensemble de test sur lequel tester le modèle.

#define the predictor variables and the response variable
X = data[['student', 'balance', 'income']]
y = data['default']

#split the dataset into training (70%) and testing (30%) sets
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=0)  

Étape 4 : Ajuster le modèle de régression logistique

Ensuite, nous utiliserons la fonction LogisticRegression() pour ajuster un modèle de régression logistique à l’ensemble de données :

#instantiate the model
log_regression = LogisticRegression()

#fit the model using the training data
log_regression.fit(X_train,y_train)

#use model to make predictions on test data
y_pred = log_regression.predict(X_test)

Étape 5 : Diagnostics du modèle

Une fois que nous avons ajusté le modèle de régression, nous pouvons alors analyser les performances de notre modèle sur l’ensemble de données de test.

Tout d’abord, nous allons créer la matrice de confusion pour le modèle :

cnf_matrix = metrics.confusion_matrix(y_test, y_pred)
cnf_matrix

array([[2886,    1],
       [ 113,    0]])

De la matrice de confusion, nous pouvons voir que :

• #Vraies prédictions positives : 2886
• #Vraies prédictions négatives : 0
• #Prédictions fausses positives : 113
• #Fausses prédictions négatives : 1

Nous pouvons également obtenir la précision du modèle, qui nous indique le pourcentage de prédictions de correction effectuées par le modèle :

print("Accuracy:",metrics.accuracy_score(y_test, y_pred))l

Accuracy: 0.962

Cela nous indique que le modèle a fait la bonne prédiction quant à savoir si un individu ferait ou non défaut de paiement dans 96,2 % des cas.

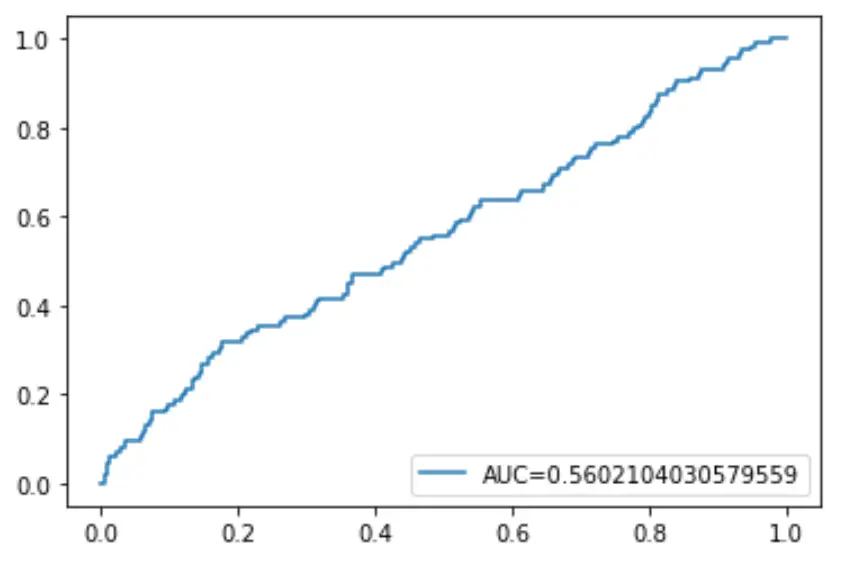
Enfin, nous pouvons tracer la courbe ROC (Receiver Operating Characteristic) qui affiche le pourcentage de vrais positifs prédits par le modèle lorsque le seuil de probabilité de prédiction est abaissé de 1 à 0.

Plus l’AUC (aire sous la courbe) est élevée, plus notre modèle est capable de prédire avec précision les résultats :

#define metrics
y_pred_proba = log_regression.predict_proba(X_test)[::,1]
fpr, tpr, _ = metrics.roc_curve(y_test,  y_pred_proba)
auc = metrics.roc_auc_score(y_test, y_pred_proba)

#create ROC curve
plt.plot(fpr,tpr,label="AUC="+str(auc))
plt.legend(loc=4)
plt.show()